* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 4.6 Isosceles and Equilateral Triangles
Multilateration wikipedia , lookup
Regular polytope wikipedia , lookup
Golden ratio wikipedia , lookup
Tessellation wikipedia , lookup
Four color theorem wikipedia , lookup
Rational trigonometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Euler angles wikipedia , lookup
History of trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Pythagorean theorem wikipedia , lookup
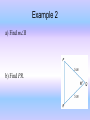
Warm Up • Explain what information you would need to prove two triangles congruent. Draw an example to help guide your response. I will be asking for people to share their responses! (and I will be collecting this). 4.6 Isosceles and Equilateral Triangles Isosceles Triangle Properties • The two congruent sides are called the legs of an isosceles triangle, and the angle with the sides that are the legs is called the vertex angle. The side of the triangle opposite the vertex angle is called the base. The two angles formed by the base and the congruent sides are called the base angles. 1 is the vertex angle. 2 and 3 are the base angles. Isosceles Triangle Theorems Example 1 • a) Name two unmarked congruent angles. • b) Name two unmarked congruent segments. Example 1 Continued c) Which statement correctly names two congruent angles? a) PJM @ PMJ b) JMK @ JKM c) KJP @ JKP d) PML @ PLK Equilateral Triangle Corollaries • The Isosceles Triangle Theorem leads to two corollaries about the angles of an equilateral triangle. Example 2 a) Find mR b) Find PR. Example 3 • You can use the properties of equilateral triangles and algebra to find missing values. • Find the value of each variable. Example 4 Prove using a two-column proof. Given: HEXAGO is a regular polygon. ∆ONG is equilateral N is the midpoint of GE EX || OG Prove: ∆ENX is equilateral. Exit Slip Write a two-column proof. Given: DE || BC 1 @ 2 Prove: AB @ AC