* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Triangle Congruence
Survey
Document related concepts
Transcript
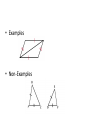
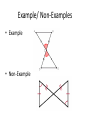
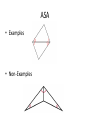
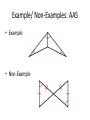
GO GIANTS! Pick up notes and the Exploration Activity Tonight’s HW: 1. P 245 # 1-7 2. P 256 #1-8 3. Make notecards from U2L8 and U2L10 (definition one side and vocab. word on the other side Agenda Review Transformation Test Exploration Activity! 4.4: SSS and SAS 4.5: AAS ASA HL Proof Practice! Stand Up! Transformation Test Results Overall, I am very proud of each and everyone of you for putting your best effort into the test. 1st Period o Average 27.1 out of 34 o 80% 6th Period o Average 28.7 out of 31 o 84% • You will get the tests back sometime this week. I still have students who need to take it! • The scores are on Infinite Campus Learning Objective(s) By the end of this period you will be able to: ① SWBAT prove triangles congruent by using SSS, SAS, ASA, AAS, and HL Exploration Activity In order to prove that triangles are congruent you need to show that: 1) All the angles are congruent 2) All the sides are congruent However, there are five shortcuts! We will be investigating these with your table-mates. Exploration Activity With your table, fill out the following worksheet. You will need 1) A straightedge 2) A protractor If you do not have the following, you will lose participation points. Triangle Congruence Activity Expectations: • You will work as a table. Everyone must be on the same problem. • You as a team are responsible for keeping one another on task. o I do not want to hear off topic discussions. • You will discuss with your tablemates. o “What did you get for the angle measures?” o “Why are my sides different from yours?” SSS and SAS Congruence (4.4) Instead of having to prove that all sides and angles are congruent in order to prove that triangles are congruent, we are going to learn 5 shortcuts. There are five ways to prove triangles are congruent: 1. SSS 2. SAS 3. ASA 4. AAS 5. HL Right now, we are going to discuss SSS and SAS. 4-4 Triangle Congruence: SSS and SAS Side–Side–Side Congruence (SSS) • If the sides of one triangle are congruent to the sides of a second triangle, then the triangles are congruent. • We abbreviate Side-Side-Side Congruence as SSS. What is a possible congruent statement for the figures? • Examples • Non-Examples 4-4 Triangle Congruence: SSS and SAS Included Angle • An angle formed by two adjacent sides of a polygon. • B is the included angle between sides AB and BC. Whiteboards 1. What is the included angle between the sides BC and CA? 2. What are the sides of the included angle A? Side-Angle-Side Congruence Side–Angle–Side Congruence (SAS) • If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent. What is the possible congruence statement for the figures? Example/ Non-Examples • Example • Non-Example 4-4 Triangle Congruence: SSS and SAS Example 1: (a) Explain why ∆ABC ∆DBC. Use the following sentence frame: It is given that ____ ____ and __ ______ By the ___________________________, ____ _____. Therefore ________ _________ by ________ 4-4 Triangle Congruence: SSS and SAS Example 1(b) : Explain why ∆XYZ ∆VWZ. It is given that ____ ____ and __ ______ By the __________________________________________, ____ _____. Therefore ________ _________ by ________ Whiteboards Explain why ∆ABC ∆CDA. It is given that ____ ____ and __ ______ By the ___________ ____________ of Congruence, ____ _____. Therefore ________ _________ by ________ Whiteboards Explain why ∆ABC ∆DBC. I am not going to to give you the sentence frame, but I still want you to use complete sentences. Follow what you have on your notes. It is given that BA BD and ABC DBC. By the Reflexive Property of , BC BC. So ∆ABC ∆DBC by SAS. Example 2: Verifying Triangle Congruence Show that the triangles are congruent for the given value of the variable. ∆MNO ∆PQR, when x = 5. PQ MN, QR NO, PR MO ∆MNO ∆PQR by SSS. Whiteboards Show that the triangles are congruent for the given value of the variable. ∆STU ∆VWX, when y = 4. ST VW, TU WX, and T W. ∆STU ∆VWX by SAS. 4-4 Triangle Congruence: SSS and SAS Example 3: The Hatfield and McCoy families are feuding over some land. Neither family will be satisfied unless the two triangular fields are exactly the same size. You know that BC is parallel to AD and the midpoint of each of the intersecting segments. Write a two-column proof that will settle the dispute. . Given: BC || AD, BC AD Prove: ∆ABC ∆CDB Proof: Closure Questions Which postulate, if any, can be used to prove the triangles congruent? In one sentence tell why or why not the triangles are congruent. 1. 2. Math Joke of the Day • What do you call a broken angle? • A rectangle! Change it to 4.5 • On top of your 4.4 Triangle Congruence: ASA< AAS, and HL please change it to 4.5 4.5 Triangle Congruence: SSS and SAS There are five ways to prove triangles are congruent: 1. SSS earlier today ( or on Wednesday – per 6) 2. SAS 3. ASA Today! 4. AAS 5. HL Included Side • Earlier, we learned what an included angle is. What do you think an included side would be? Included side • common side of two consecutive angles in a polygon. 4-4 Triangle Congruence: SSS and SAS Angle–Side–Angle Congruence (ASA) • If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent • . What is a possible congruent statement for the figures? ASA • Examples • Non-Examples Angle-Angle-Side Congruence Angle-Angle-Side(AAS) • If two angles and a non-included side of one triangle are congruent to the corresponding angles and a side of a second triangle, then the two triangles are congruent. What is the possible congruence statement for the figures? Example/ Non-Examples: AAS • Example • Non-Example Example 1 (a) Example 1: (a) Explain why ∆UXV ∆WXV. It is given that ____ ____. ________ is a right angle so ______ is also a right angle by ______________. Therefore, ____________ ____________. (add this sentence frame into your notes) By the __________________________________________, ____ _____. Therefore ________ _________ by ________ Example 1 (b) Example 1: (b) Explain why ∆ECS ∆TRS. This time, I am not going to give you a sentence frame, but I still want you to use COMPLETE SENTENCES to explain why the triangles are congruent. Whiteboard Determine if you can use ASA to prove NKL LMN. Explain. By the Alternate Interior Angles Theorem. KLN MNL. NL LN by the Reflexive Property. No other congruence relationships can be determined, so ASA cannot be applied. Whiteboard! On your whiteboard, draw a right triangle 1. Label the legs of the triangle 2. Label the hypotenuse Hypotenuse-Leg (HL) Congruence Hypotenuse-Leg Congruence (HL) • If the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent. • IMPORTANT: The hypotenuse is ALWAYS across from the right angle ( highlight this in your notes) Examples/Non-Examples: HL • Example • Non-Example Whiteboards Identify the postulate or theorem that proves the triangles congruent. HL ASA SAS or SSS Example 2 Proof Practice! Whiteboard Flash! I am going to show you two triangles You are going to write down whether they are congruent by SSS, SAS, AAS, ASA, or HL! Once your entire table thinks they have it correct, STAND UP! First table to have ALL their members stand up with the correct statement wins that round. Note: The triangles might not be congruent. If so, state they are not congruent. A) SSS C) AAS B) SAS D) ASA 9) A) ASA C) SAS B) AAS D) SSS A) Not congruent C) SAS B) ASA D) SSS 10) A) SSS C) SAS B) Not congruent D) ASA A) SAS C) SSS B) AAS D) ASA 6) A) Not congruent C) ASA 8) B) SSS D) AAS A) Not congruent C) ASA B) SSS D) AAS 8) A) Not congruent C) SAS 10) B) ASA D) SSS A) AAS C) SSS B) SAS D) ASA 7) A) SSS C) AAS 9) B) SAS D) ASA congruent A) SSS C) Not congruent B) AAS D) ASA 14) B) SAS D) ASA A) SAS C) AAS 16) B) Not congruent D) SSS A) SAS C) SSS B) Not congruent D) ASA 18) A) AAS C) SAS B) Not congruent D) SSS A) ASA C) Not congruent B) AAS D) SAS 19) A) SAS C) Not congruent B) SSS D) AAS 22) B) AAS D) SAS A) Not congruent C) AAS 24) B) SAS D) ASA 23) A) AAS C) Not congruent B) SAS D) SSS A) Not congruent C) AAS B) SA D) AS 24) A) ASA C) AAS B) Not congrue D) SAS A) SSS C) AAS 10) B) ASA D) SAS A) AAS C) Not congruent B) ASA D) SAS SSS ASA uent A) SSS C) Not congruent 16) B) ASA D) SAS A) Not congruent C) ASA B) SAS D) AAS A) LL C) AAS B) LA D) ASA 12) A) HL C) SAS B) HA D) Not congruent A) ASA C) SAS B) HA D) AAS 13) A) ASA C) HA 15) B) HL D) SAS A) SSS C) HL B) HA D) ASA 23) A) SAS C) ASA B) AAS D) Not congruent A) AAS C) HL B) LL D) Not congr 7) A) Not congruent C) HA B) H D) S 11) A) AAS C) ASA B) HA D) LA 20) A) SAS C) ASA 22) B) LA D) LL Part II: Missing Info State what additional information is required in order to know that the triangles are congruent for the reason given.