* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 14: Capacitors in Series and Parallel
Survey
Document related concepts
Transcript
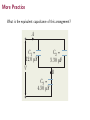
Electricity and Magnetism Circuits Capacitors in Series and Parallel Lana Sheridan De Anza College Oct 13, 2015 Last time • Capacitance • capacitors of different shapes Warm Up Question True or false: A component (fixed) capacitor has a capacitance, even when storing no charge. (A) true (B) false Warm Up Question True or false: A component (fixed) capacitor has a capacitance, even when storing no charge. (A) true (B) false ← Overview • Parallel plate capacitors • Circuits and circuit diagrams • Capacitors in series and parallel • Energy stored in a capacitor Capacitance Q = C (∆V ) ⇒ C = Q ∆V C is a property of the geometry of the capacitor. A particular capacitor will have a particular fixed value of C , just like a given resistor will have a constant value of resistance R. For a parallel plate capacitor: C= 0 A d where d is the separation distance of the plates and A is the area of each plate Circuits Circuits consist of electrical components connected by wires. Some types of components: batteries, resistors, capacitors, lightbulbs, LEDs, diodes, inductors, transistors, chips, etc. The wires in circuits can be thought of as channels for an electric field that distributes charge to (or charge flow through) the components. Circuit substitution problem. of is superconducting magne Notice that this the as Equation 26.2 Notice that thisexpression expression is the samesame asthis Equation 26.2, the capa Capacitor section. Th approximately ten times g component symbols symbol initially unchar Use Equation 30.17 to express the magnetic field in the tromagnets. Such superco In Supercond studying e storing energy. interior of the base solenoid: 26.3circuit Combinations resonance imaging, or MR diagram " Battery 26.3 Combin Find the mutual inductance, noting that magnetic Twothe or more capacitors oftenfo a organs without the need elements. The symbol battery ∆V the equivalent capacitance of c ! coil caused flux F BH through the handle’s by the magful radiation. orThroughout more capacito Capacitor this Two section. this se wires between symbol initially theuncharged. equivalent capac netic field the base coil is BA: The of direction of the effective flowCapacitor of positive and switches asw In studying electric circuits, this section. Through diagram. Such The a diagra "a number circuit Switch Wireless charging is used ofinitially other “cordless” ds Battery in ure 26.6. Open charge is clockwise. capacitor Csymbol 27.6 Electrical elements. Theuncharged. circuit symbolsP symbol ! symbol used by some manufacturers of electricwires cars that avoids model for a dire cap In studying electric between the circuit elem I andcircuit switches as wellcircuits, as theSuch colo diagram. In typical electric ing apparatus. Closed is at the higher " Battery Switch ure 26.6. The symbol for the ca Open elements. The circuit a source such as a battery symbol model for a capacitor, a pair of ! switch Figure 26.6 Ssymbol CircuitClosed symbols forisdetermine between the atwires the higher potential and ci is r Let’s an express batteries, and switches. Parallel Com and switches as well b capacitors, c symbols Figure 26.6 Circuit for transfer. First, consider thea capacitors, batteries, and Parallel Combination Notice that capacitors areswitches. in Switch ureTwo 26.6. The symbol # Open capacitors to a resistor. (Resistors are Notice that capacitors are in Rin green, Two capacitors as sho !V batteries blue, are and symbol model forconnected a capacitor blue, resistor R batteries are in green, andconnecting " wires also have nation of capacitors. Figure 26. nation of capac switches are in red. The closed switches are in red. The closed Closed is at the higher poten a d whereas capacitors. The left plates of the switch can carry current, some to the resistor. Unles capacitors. The switch can whereas the battery by a conducting wire thecarry open onecurrent, cannot. ! Figure 26.6 Circuit symbols for ais capacitor When is conn wires small the open one batteries, cannot. the compared battery bywit a C L capacitors, and switches. Parallel Combinat " inductor L delivered to the wires is ne combination is an LC circu Q max Notice that capacitors are in Two capacitors following acurr pos blue, batteries are in green,then and Imagine closed, both theconne Figure 27.11 A circuit consistnation of capacitors. switches are in red. The closedcircuit in Figure 27.11 from late between maximum p ing of a resistor of can resistance R capacitors. The left pl switch carry current, whereas We identify the entire circu S and a battery having a potential cuit is zero, no energy is tr the open one cannot. 32.5 Oscillations the battery by a condu this sectio initially u In stud circuit di " Battery elements. symbol ! wires bet and Batteries cause a potential difference between two parts of the switc circuit. Switch ure 26.6. Open This drives a charge flow. symbol model for Closed is at the h Circuits: Batteries Capacitor symbol 8 Circuits HALLIDAY REVISED The different elements can be combined together in various ways to make complete circuits: paths for current to flow from one terminal of a battery or power supply to the other. l h + B C Terminal C l h + B– V – S (a ) S Terminal (b) This circuit is said to be incomplete while the switch is open. 25-4 (a) Battery B, switch S, and plates h and l of capacitor C, connected in a cir- (b) A schematic diagram with the circuit elements represented by their symbols. negative charges moving horizontally Flow of charge in a circuit gureConventional 27.4. Rank the current in these four current is said to flow from the positive terminal to the negative terminal. However, actually it is negatively charged electrons that flow through metal wires: # " " # # # − c 1 ← d current, i ← Figure from Serway and Jewett, 9th ed. + Series and Parallel Series Parallel When components are connected one after the other along a single path, they are connected in series. When components are connected side-by-side on different paths, they are connected in parallel. R1 V V R2 R1 R2 + B– es stored on all the capacitors. Capacitors in Parallel V –q 3 C 3 V –q 2 C Capacitors parallel all haveitthe same potential difference T 3 (a) PA R Terminal in parallel, weincan simplify with across them. N PARALLEL AND IN SERIES Parallel c their equi Equivalent circuit: the same 663 Three capacitors in parallel: Terminal capacitor that d with an equivalent l difference V as the actual + B– +q 3 V –q 3 C 3 V +q 2 –q 2 C 2 V +q 1 V –q 1 C 1 + B– +q V –q Ceq (b) nsense word “par-V,” which is close (a) Terminal e the same V.”) Figure 25-8b shows Fig. 25-8 (a) Three capa Parallel capacitors and We could all three capacitors with one acitance Ceq)replace that has replaced thein theincircuit parallel to battery B. The their equivalent have equivalent capacitance. The current and potential difference in the C2, and C3) of Fig. 25-8a. tains potential difference V same V (“par-V”). rest of the circuit the is unchanged by this. -8b, we first use Eq. 25-1 to find the nals and thus across each ca + +q equivalent capacitor, with c + B– es stored on all the capacitors. Capacitors in Parallel V –q 3 C 3 V –q 2 C Capacitors parallel all haveitthe same potential difference T 3 (a) PA R Terminal in parallel, weincan simplify with across them. N PARALLEL AND IN SERIES Parallel c their equi Equivalent circuit: the same 663 Three capacitors in parallel: Terminal capacitor that d with an equivalent l difference V as the actual + B– +q 3 V –q 3 C 3 V +q 2 –q 2 C 2 V +q 1 V –q 1 C 1 + B– +q V –q Ceq (b) nsense word “par-V,” which is close (a) Terminal e the same V.”) Figure 25-8b shows Fig. 25-8 (a) Three capa Parallel capacitors and We could all three capacitors with one acitance Ceq)replace that has replaced thein theincircuit parallel to battery B. The their equivalent have equivalent capacitance. The current and potential difference in the C2, and C3) of Fig. 25-8a. tains potential difference V same V (“par-V”). rest of the circuit the is unchanged by this. -8b, we first use Eq. 25-1 to find the nals and thus across each ca What would be the capacitance of this equivalent capacitor? equivalent capacitor, with c +q + Capacitors in Parallel Capacitors in parallel all have the same potential difference across them. ∆V1 = ∆V2 = ∆V3 = ∆V The total charge on the three capacitors is the sum of the charge on each. qnet = q1 + q2 + q3 where q1 = C1 ∆V . Capacitance is C = q/(∆V ): Ceq = qnet ∆V Capacitors in Parallel Equivalent capacitance: Ceq = = qnet ∆V q2 q3 q1 + + ∆V ∆V ∆V = C1 + C2 + C3 Capacitors in Parallel Equivalent capacitance: Ceq = = qnet ∆V q2 q3 q1 + + ∆V ∆V ∆V = C1 + C2 + C3 So in general, for any number n of capacitors in parallel, the effective capacitance of them all together is: Ceq = C1 + C2 + ... + Cn = n X i=1 Ci + B– Capacitors in Series +q V2 V –q C 2 Capacitors in series all store the same charge. 664 CHAPTER 25 CAPACITANCE Three capacitors in series: Terminal +q V1 + B– –q C 1 +q V V2 –q C 2 +q V3 Terminal (a) +q V3 –q C 3 produces charge ! negative charge fr Terminal Series c repelled negative Equivalent circuit: (a) their equ charge !q). That the the same charge from to +q plate of capacitor + B – V of capacitor 1 help –q C battery,eqleaving th Here are two (b) 1. When charge is (a) Three capac it can move alo nected in series to battery B. Fig. 25-9a. If the Series capacitors and maintains 2. potential differenc The battery di their equivalent have –q C 3 Fig. 25-9 Capacitors in Series Again, we could replace all three capacitors in the circuit with one equivalent capacitance and we can find the capacitance of this equivalent capacitor. The sum of the potential differences across capacitors in series is V , the battery’s supplied potential difference. ∆V = ∆V1 + ∆V2 + ∆V3 where ∆V1 = q/C1 , etc. Then, Ceq = q ∆V Capacitors in Series Equivalent capacitance: Ceq = q ∆V q ∆V1 + ∆V2 + ∆V3 V1 + V2 + V3 −1 = q ∆V1 ∆V2 ∆V3 −1 = + + q q q 1 1 −1 1 = + + C1 C2 C3 = Capacitors in Series In general, for any number n of capacitors in series, we can always relate the effective capacitance of them all together to the individual capacitances by: n X 1 1 1 1 1 = + + ... + = Ceq C1 C2 Cn Ci i=1 The equivalent capacitance of capacitors in series is always less than the smallest capacitance in the series. Practice A 5.0 µF capacitor is connected in parallel with a 10 µF capacitor. What is the equivalent capacitance of this arrangement? Practice A 5.0 µF capacitor is connected in parallel with a 10 µF capacitor. What is the equivalent capacitance of this arrangement? Ceq = 15 µF Practice A 5.0 µF capacitor is connected in parallel with a 10 µF capacitor. What is the equivalent capacitance of this arrangement? Ceq = 15 µF A 5.0 µF capacitor is connected in series with a 10 µF capacitor. What is the equivalent capacitance of this arrangement? Practice A 5.0 µF capacitor is connected in parallel with a 10 µF capacitor. What is the equivalent capacitance of this arrangement? Ceq = 15 µF A 5.0 µF capacitor is connected in series with a 10 µF capacitor. What is the equivalent capacitance of this arrangement? Ceq = 3.3 µF We first reduce the The equival circuit to a single parallel cap What is the equivalent capacitance of this arrangement? capacitor. is larger. More Practice A A C1 = 12.0 µ F V C 12 17.3 C2 = 5.30 µ F B C3 = 4.50 µ F (a) V C3 4.50 (b) citance More Practice When solving this type of problem, take an iterative approach. Identify sets of capacitors that are in parallel, then series, then parallel, etc. and at each step replace with the equivalent capacitance: citance and b for the ure 26.9a. All 4.0 1.0 4.0 4.0 3.0 6.0 a lly and make re connected. allel connec- 2.0 a b a b 8.0 8.0 b 8.0 heyMore can be Practice connected in series or apacitance for the combination, n parallel waytype because When(c) either solving this of problem, take an iterative approach. Identify sets of capacitors that are in parallel, then series, then parallel, etc. and at each step replace with the equivalent capacitance: r the . All 4.0 4.0 4.0 2.0 3.0 6.0 a make cted. nec- ains 1.0 2.0 a b a b 8.0 8.0 b b a 6.0 b a 8.0 4.0 c d Figure 26.9 (Example 26.3) To find the equivalent capacitance We first reduce the The equival More Practice circuit to a single parallel cap What is the equivalent capacitance of this arrangement:is larger. capacitor. A A C1 = 12.0 µ F V C 12 17.3 C2 = 5.30 µ F B C3 = 4.50 µ F (a) V C3 4.50 (b) We first reduce the The equival More Practice circuit to a single parallel cap What is the equivalent capacitance of this arrangement:is larger. capacitor. A A C1 = 12.0 µ F V B C3 = 4.50 µ F Ceq = 3.57 µF. C 12 17.3 C2 = 5.30 µ F (a) V C3 4.50 (b) Energy Stored in a Capacitor A charged capacitor has an electric field between the plates. This field can be thought of as storing potential energy. As you might expect, the energy stored is equal to the work done charging the capacitor. (Energy Conservation!) 26.4 Energy Stored in a Charged Capacitor Energy Stored in a Capacitor 787 charged capacitor has an electric field between the plates. at occurs,Athere is a transformation s closed,field energycan is stored as chemi- of as storing potential energy. be thought is transformed during the chemical is operating in an electric circuit. al potential energy in the battery is mightof expect, ated withAs theyou separation positive the energy stored is equal to the work charging the capacitor. (Energy Conservation!) This done or, we shall assume a charging proThe work required to move charge cribed in Section 26.1 but that gives dq through the potential ed because the energy in the final difference !V across the capacitor But process. how much work done? Wapproximately 3 Imagine app = q ∆V is given by , yet the potential arge-transfer the is plates the areacharge of the shaded rectangle. on the capacitor plates. u transfer the charge changes mechanically difference as more is placed s. You grab a small amount of posi!V causes this positive charge to move k on the charge as it is transferred required to transfer a small amount t once this charge has been transen the plates. Therefore, work must s potential difference. As more and the other, the potential difference ed. The overall process is described q uation 8.2 reduces to W 5 DU E ; the Q t appears as an increase in electric me instant during the charging pro- dq dq through the potential gy in the final difference !V across the capacitor Energy Stored in a Capacitor .3 Imagine the plates is given approximately by area of the shaded rectangle. How much workthe is done? dWapp = (∆V ) dq e mechanically mount of posi!V harge to move is transferred small amount as been transore, work must e. As more and tial difference ess is described q W 5 DU E ; the Q ase in electric dq charging pro→ Need to integrate! Figure 26.11 A plot of potential or is DV 5 q/C. Energy Stored in a Capacitor q C For a fixed capacitor (plates are not changing configuration or shape), C is a constant. ∆V = ZQ UE = Wapp = = q dq 0 C 1 Q2 2 C The energy stored in a capacitor with charge Q and capacitance C : 1 Q2 U= 2 C Energy Stored in a Capacitor The energy stored in a capacitor with charge Q and capacitance C : 1 U= 2 Q2 C Since Q = C (∆V ) we can also write this as: 1 U = C (∆V )2 2 And: 1 U = Q ∆V 2 Stored Energy Example Suppose a capacitor with a capacitance 12 pF is connected to a 9.0 V battery. What is the energy stored in the capacitor’s electric field once the capacitor is fully charged? Stored Energy Example Suppose a capacitor with a capacitance 12 pF is connected to a 9.0 V battery. What is the energy stored in the capacitor’s electric field once the capacitor is fully charged? UE = 4.9 × 10−10 J Energy Density It is sometimes useful to be able to compare the energy stored in different charged capacitors by their stored energy per unit volume. We can link energy density to electric field strength. This will make concrete the assertion that energy is stored in the field. Energy Density It is sometimes useful to be able to compare the energy stored in different charged capacitors by their stored energy per unit volume. We can link energy density to electric field strength. This will make concrete the assertion that energy is stored in the field. For a parallel plate capacitor, energy density u is: uE = UE Ad (Ad is the volume between the capacitor plates.) Energy Density and Electric Field uE = = UE Ad C (∆V )2 2Ad Energy Density and Electric Field uE = = Replace C = UE Ad C (∆V )2 2Ad 0 A d : uE = = 0 A ∆V 2 d 2Ad 0 ∆V 2 2 d Energy Density and Electric Field uE = = Replace C = UE Ad C (∆V )2 2Ad 0 A d : uE = = 0 A ∆V 2 d 2Ad 0 ∆V 2 2 d Lastly, remember ∆V = Ed in a parallel plate capacitor, so: 1 uE = 0 E 2 2 Energy Density and Electric Field Energy density in a capacitor: 1 uE = 0 E 2 2 The derivation of this expression assumed a parallel plate capacitor. However, it is true more generally. (General proof requires vector calculus.) It is also true for varying electric fields, in which case the energy density varies. Energy density of an electric field ∝ E 2 Summary • parallel plate capacitors • circuits, circuit diagrams • capacitors in series and parallel • practice with capacitors in circuits • energy stored in a capacitor Homework Serway & Jewett: • PREVIOUS: Ch 26, onward from page 799. Problems: 1, 5, 7, 11, 51 • NEW: Ch 26. Problems: 13, 17, 21, 25, 31, 33, 35

















































![Sample_hold[1]](http://s1.studyres.com/store/data/008409180_1-2fb82fc5da018796019cca115ccc7534-150x150.png)




