Download Statistics for Dummies

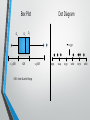
Statistics for
Dummies Workshop
**You’re not really Dummies**
Before Starting
• Disclaimer: We can’t teach a whole quarter of statistics, but we can teach
you how to study. Studying for statistics requires reading the book!
• If you are not reading on your own and just taking notes in class, you are
likely not to succeed
• Upper Level classes will automatically assume you have learned to study the
material
• DO NOT Chegg or Google the solutions
What’s going to be covered
• Diagrams
• Data Summary and Presentation
• Binomial distribution
• Engineering/Statistics Toolbox
• Z-test
•
Type 2 Error
• T-test
• C2 Test
Dot Diagram
Box Plot
Q1
Q2
Q3
x = 1550
1.5 IQR
IQR
IQR = Inter Quartile Range
1.5 IQR
1030
1040
1050
1060
1070
1080
Histogram
Frequency
Cumulative Frequency
25
70
60
20
50
15
40
30
10
20
5
10
0
20
30
40
50
60
70
80
0
20
30
40
50
60
70
80
Data Summary
Stem and Leaf Diagram
Correlation
Coefficient
n
R=
S
i=1
(xi – x)(yi – y)
n
(S )( S
n
(xi – x)2
i=1
i=1
)
(yi – y)2
Stem
1
2
3
4
5
7
8
Leaf
3
245
36814
4624563
5252
4
Freq.
1
3
5
7
4
0
1
Quartile/Percentile Calculation
Quartile
1st
(n + 1)
4
2nd
2(n + 1)
4
3rd
3(n + 1)
4
Percentile
5th
.05(n + 1)
95th
.95(n + 1)
Value will give ordered
observation
Interpolate as needed
Binomial Distribution
P(X = x) =
( ) p (1-p)
n!
( ) = x!(n – x)!
n
x
n
x
x
n-x
We use Binomial Distribution when:
1. Trials are independent
2. Each trial results in one of two possible
outcomes, success or failure ooooh!
3. The probability, p, remains constant
Engineering/Statistics Toolbox
•
Known as the procedure for hypothesis testing
Steps for Generic Hypothesis Testing
•
•
•
•
•
•
1. Identify Parameter Of Interest:
•
For instance; determine the saltiness of a potato chips
2. State the Null Hypothesis (H0):
•
Standard that you are testing against, like the given average students test scores
3. Alternative Hypothesis (H1):
•
Specify an appropriate alternative hypothesis
4. Test Statistic
•
Equation you are going to use for each test. Z = X-m/(s/n^.5)
6. Computations
•
Plug and chug
7. Conclusion
•
Decide whether the Null Hypothesis should be rejected and report and that in the problem context.
Z-Test
• When do you use it?
•
•
Known mean and known variance
Gives the probability density of when something is going to happen
• Most of the time an alpha value will be given to you
•
If not, assume 0.05
Type II Error
•
•
•
•
When you fail to reject the null hypothesis when it is wrong then you have
committed a type II error
b = f(Z0)
Power = 1 - b
For instance:
Say you have a pop. of 50 beads with an average diameter of 10 mm (actual average
diameter). However, your sample of 10 beads has an average of 15 mm. You want to
confirm that a null hypothesis of 15 inches is correct. If you fail to reject the null you
messed up.
T-Test
• Unknown variance and known mean
• You need to determine the sample variance
• You need to know degrees of freedom
• That will be n-1, (n is the sample size)
• Literally the same as the Z-test except with degrees of freedom
and sample variance
C2-Test
• This is a test on the sample variance
• Much the same as T-test
• Must know the sample variance, as well as the actual variance
• This tests variance, NOT standard deviation