* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 1
Survey
Document related concepts
Transcript
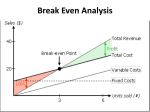
Linear Functions Chapter 1 Linear Functions 1.2 Linear Functions and Applications Equations of Lines Equation Description ax by = c Standard form: a 0, b 0, x-intercept = c/a, y-intercept = c/b, m = –a/b. y = mx + b Slope-intercept form: slope m, y-intercept b y – y1 = m(x – x1) Point-slope form: slope m, line passes through (x1,y1) Slopes of Lines Undefined slope (Vertical line) m=0 (Horizontal line) 1.2 Applications of Linear Functions Many situations involve two variables, x (independent variable) and y (dependent variable), with a linear relationship. If y is expressed in terms of x, then y is a linear function of x. For any value of x, the corresponding value of y can be calculated. Linear Functions Examples y = 3x + 7 12x + 6y = 24 y = -2x + 4 f(x) Notation: Letters can be used to name functions. if f is used to name y = 3x + 7 f(x) = 3x + 7 f(2) = 3(2) + 7 = 13 f(-2) = 1, f(0) = 7, f(1) = 10... Linear Functions A relationship f defined by y = f(x) = mx + b, for real numbers m and b, is a linear function Applications of Linear Functions Basic business relationships: Revenue = Price Quantity Total Cost = Fixed Costs + Variable Costs Average Cost = Total Cost ÷ Quantity Profit = Revenue – Total Costs Linear Functions y mx b y is the dependent variable. y x is the independent variable. Therefore, changes in x result in changes in y. x Supply and Demand Economists normally plot price (p) on the vertical axis, and quantity (q) on the horizontal axis. Demand function D(q): p m qd b p b qd m Quantity Supply and Demand Economists normally plot price (p) on the vertical axis, and quantity (q) on the horizontal axis. Supply function S(q): p m qs b p b qs m Quantity Supply and Demand Example Quantity demanded D(q): p = – ¾ q + 60 (20, 45) Calculate quantity demanded at $45 and $18 p b 45 60 20 qd m 3 4 (20, 45) Quantity Supply and Demand Example Quantity demanded D(q): p = – ¾ q + 60 (20, 45) Calculate quantity demanded at $45 and $18 (56, 18) p b 18 60 56 qd m 3 4 (56, 18) Quantity Supply and Demand Example p = – ¾q + 60 (80, 60) (20, 45) Quantity supplied: S(q) p = ¾q Calculate quantity supplied at $60 and $12 (56, 18) p b 60 0 80 qS 34 m (80, 60) Quantity Supply and Demand Example p = – ¾q + 60 (80, 60) (20, 45) p=¾q (56, 18) (16, 12) Quantity supplied: S(q) p = ¾q Calculate quantity supplied at $60 and $12 p b 12 0 16 qS 34 m (12, 16) Quantity Market Equilibrium Equilibrium p = 60 – ¾ q p=¾q (40, 30) Quantity The market is in equilibrium when qd = qs Equilibrium quantity: 60 – ¾ q = ¾ q 240 – 3q = 3q 240 = 6q (40, 30) 40 = q Equilibrium price: p = 3/4 (40) p = 30 Market Equilibrium S Surplus Equilibrium Shortage Quantity D Short-Run Cost Analysis Fixed costs Variable costs Constant in the short run Do not change with changes in output Per item costs (labor, materials, etc) Change with changes in output. Marginal cost The change in total cost from a one-unit change in output. Short-Run Cost Analysis The cost of mowing lawns: C(x) = 8x + 325 C(x) is the cost in dollars to mow x lawns. The cost of mowing 0 lawns is C(0) = 8(0) + 325 = $325.00 $325.00 = fixed costs C(1) = 8(1) + 325 = $333.00 C(2) = 8(2) + 325 = $341.00 Short-Run Cost Analysis C(x) = 8x + 325 m=8 Marginal cost = $8.00 COST FUNCTION In a cost function of the form C(x) = mx + b, the m represents the marginal cost per item and b the fixed cost. Conversely, if the fixed cost of producing an item is b and the marginal cost is m, then the cost function C(x) for producing x items is C(x) = mx + b Short-Run Cost Analysis Assume that the marginal cost to make x items of a product is $90, and that 150 items cost $16,000 to produce. Find the cost function given it is linear. C x 90 x b 16, 000 90 150 b 16, 000 13,500 b 2,500 b C x 90x 2500 Short-Run Cost Analysis Given the cost function C(x) = 90x + 2500, Calculate the average cost (per-item cost) of producing 1000 items. C 1000 C x C 1000 C x 1000 x Short-Run Cost Analysis Given the cost function C(x) = 90x + 2500, Calculate the average cost (per-item cost) of producing 1000 items. 90 1000 2500 C 1000 $92.50 1000 Break-Even Analysis Total revenue = Price(p) Quantity(x) Profit = total revenue – total cost R(x) = px P(x) = R(x) – C(x) Break-even quantity: The output at which total revenue = total cost. Break-even point: The corresponding ordered pair (x, p). Break-Even Analysis The cost function C(x) for a firm that produces x units of poultry feed is: C(x) = 20x + 100 The price of the feed is $24 per unit How many units must be sold for the firm to break even? What is total revenue and total cost at the break-even quantity? Break-Even Analysis C x 20 x 100 Total revenue: R x p x Break-even point: R x C x Total cost: p $24 R x 24 x 24x 20x 100 x 25 (break-even quantity) Break-Even Analysis R x C x R x 24 x 24 25 600 C x 20 x 100 20 25 100 600 Total cost at break-even quantity Break-even point: (25, 600) Now You Try The profit (in millions of dollars) from the sale of x million units of Blue Glue is given by P(x) = .7x – 25.5. The cost is given by C(x) = .9x + 25.5 a) Find the revenue equation b) What is the revenue from selling 10 million units? c) What is the break-even point? Chapter 1 End