Download Conservative forces and the potential energy function

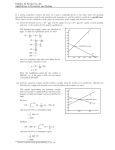
Non-conservative forces and the work-energy theorem
Consider an object falling with air-resistance. There are
two forces to consider; the gravitational force
(conservative) and the drag force (non-conservative).
1
The total work done is
W1!2 = Wc + Wnc ,
where Wc is the work done by the
2
conservative (gravitational) force and
Wnc is the work done by the non-
conservative (drag) force. But, by the work-energy
theorem
W1!2 = "K = K2 # K1.
Also Wc = #"U = #( U2 # U1 ).
$K2 # K1 = # ( U2 # U1 ) + Wnc ,
i.e., Wnc = (K2 + U2 ) # (K1 + U1 ),
or Wnc = E mech2 # E mech1 = "E mech .
Therefore, the work done by a non-conservative force is
equal to the change in mechanical energy.
Conservative forces and the potential energy function
If the potential energy of a system has a unique value at
!
every point r , we can define a potential energy function,
!
U( r ), which tells us how potential energy varies with
position.
One property of a conservative force is that the work
done by the force can be expressed as the difference
between the initial and final values of the potential
energy, i.e.,
! !
dW = F • d s = !dU,
where U is the potential energy function. Hence, the
work done by a conservative force equals the decrease in
the potential energy from point 1 to point 2.
2!
!
"#U = U2 ! U1 = ! $ F • d s .
1
! !
Since dU = ! F • d s , then, in one-dimension,
dU
dU = !Fx .dx, i.e., Fx = ! .
dx
dU
Given that Fx = ! , if we know the potential energy
dx
U(z)
function, U(x), we can determine the force Fx at any
U!
point. Conversely, if we know the functional form of Fx,
we can find the potential energy function, since
dU = !Fx .dx, i.e., U = ! " Fx .dx .
Examples ...
[1] Gravitational force:
kˆ
!
mg
Let us find the potential energy
function for the gravitational force.
We take the z-direction ( kˆ )
vertical. Then, from above, the incremental change in
potential energy as the object falls is
! !
dU = ! F • d s = !(!mg kˆ ) • (dxˆi + dyˆj + dz kˆ ) = ( mg )dz.
#U = mg " dz = mgz + U",
where U" is the reference energy when z = 0. Let’s plot
this function:
Note: U ! U(z), i.e., it has
2
1
#U = U2 " U1
Height (z)
a unique value at z. This is
the potential energy
function for the
gravitational force. Normally, we deal only with
differences in potential energy, so the choice of U! is
entirely arbitrary. Note: the force associated with this
dU
potential energy function is Fz = "
= "mg, as
dz
expected.
[2] Elastic force:
F2 = " kx
F1 = kx
If you compress a spring
a distance x in the xdirection, the force, F1,
x
you exert is given by
Hooke’s Law, i.e.,
F1 = kx, where k is the spring constant. The spring does
negative work since the force it exerts on you ( F2 = "kx)
is opposite to the displacement x.
Therefore, the elastic potential energy function U(x) is
given by:
U(x)
Equilibrium position: x !.
Stable equilibrium when
! !
dU = ! F • d s = ! ( !F2 ).dx = kx.dx.
1
"U(x) = k # x.dx = kx 2 + U" .
2
U(x ! ) is a minimum,
But, when there is no displacement, i.e., x = 0, the spring
x
x!
has zero elastic potential energy.
"U(0) = 0, so U" = 0.
d2U
i.e.,
> 0.
dx 2
U(x)
Equilibrium position: x !.
At this point, there is no net force acting on the spring (in
Unstable equilibrium when
the x-direction); we say that the spring is in equilibrium.
U(x ! ) is a maximum,
This is the definition of equilibrium, which we first came
across in chapter 4 (Newton’s 1st Law).
Equilibrium: At equilibrium
x
x!
U(x)
Equilibrium position: x !.
dU
F = 0, i.e.,
= 0,
dx
Neutral equilibrium since
U(x ! ) is an inflexion point,
so U(x) is an extremum. However, we must exercise care
dU
in using that criterion, since
= 0 does not uniquely
dx
define a minimum in the potential energy function.
d2U
i.e.,
< 0.
dx 2
x
x!
i.e.,
d2U
dx 2
= 0.
(a) To find the equilibrium positions we need F(x).
dU(x)
F(x) = !
= !6x + 6x 2 .
dx
F(x)
At equilibrium F(x) = 0,
dU(x)
i.e.,
= 6x 2 ! 6x
dx
Question 10: The potential energy of an object, confined
to move along the x-axis, is
U(x) = 3x 2 ! 2x 3 for x " 3 m,
!1
1
2
and
force acting on the object is the force associated with
this potential energy function, (a) at what positions is the
object in equilibrium and what type of equilibrium is
Therefore, the equilibrium
positions are at x = 0 and x = 1 m.
U(x) = 0 for x > 3 m,
where U(x) is in Joules and x is in meters. If the only
= 6x(x ! 1) = 0.
x(m)
To find out the type of equilibrium look at the signs of the
d 2 U(x)
seond derivative,
, at x = 0 and x = 1 m.
dx 2
d 2 U(x)
Now,
= 6 ! 12x.
dx 2
associated with each position? (b) Sketch the potential
energy function.
• At x = 0:
d 2 U(x)
dx 2
= 6 (> 0) " Stable.
d 2 U(x)
• At x = 1 m:
= !6 (< 0) " Unstable.
dx 2
(b)
U(J)
10
U(x) = 3x 2 ! 2x 3
x(m)
!1
1
!10
2