Download Unit 2 Angles, Triangles, and Trigonometry

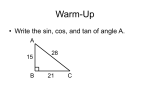
HARTFIELD – PRECALCULUS
Unit 2 Angles, Triangles, and Trigonometry
(2)
(3)
(4)
(6)
(8)
(10)
(14)
(17)
(20)
(21)
(23)
(24)
(26)
(28)
(31)
(36)
Definition of an Angle
Angle Measurements & Notation
Conversions of Units
Angles in Standard Position
Quadrantal Angles; Coterminal Angles
Arcs and Sectors of Circles
Trigonometry of Right Triangles
Solving Right Triangle
Angles of Inclination, Depression, and Elevation
Special Right Triangles
Trigonometry of Angles
Signed values of Trigonometric Ratios
Reference Angles
Reference Angles and Trigonometric Ratios
Solving Oblique Triangles
Law of Sines
Law of Cosines
Ambiguous Case of Law of Sines
UNIT 2 NOTES | PAGE 1
Know the meanings and uses of these terms:
Degree
Radian
Angle in standard position
Quadrantal angle
Coterminal angles
Sector of a circle
Reference angle
Oblique triangle
Review the meanings and uses of these terms:
Angle
Vertex of an angle
Ray
Intecepted arc
Central angle of a circle
Right triangle
Angle Sum Theorem
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 2
Definition of an Angle
(Geometric Definition)
Definition 1: The composition of two rays with a
common endpoint.
Definition 2: The result of coincident rays where
one ray has been rotated about its
endpoint.
Definition: The vertex of an angle is the endpoint
shared by the rays of the angle.
AOB at right
R1 and R2 are the rays
O is the vertex
If R2 is the ray that has been rotated out of
coincidence with R1, we say that R1 is the initial
side and R2 is the terminal side.
The measurement of an angle is quantified by the
amount of rotation from the initial side to the
terminal side. A counterclockwise rotation results
in a positive measurement while a clockwise
rotation results in a negative measurement.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 3
Angle Measurements & Notation
There are two primary units used for measuring
angles: degrees and radians.
(There is also a historically interesting but functionally irrelevant third unit called grads.)
One degree is defined to be 1/360th of a complete
rotation about a vertex. Thus an angle measuring
360 would involve the terminal side rotating
completely back into coincidence with the initial
side.
The most common symbol used to mark an angle
and identify its measurement is the Greek letter 
(theta).
One radian is defined to be a rotation in which the
intercepted arc of the unit circle is length 1. Thus
an angle measuring 2 would involve the terminal
side rotating completely back into coincidence
with the initial side; by extension, this means one
radian is exactly 1/2 of a complete rotation
about a vertex.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 4
Basic Conversions of Degrees and Radians
180 =
radians
90 =
radians
45 =
radians
30 =
radians
1 =
270 =
radians

180
radians  0.017453 radians
1 radian =
180

  57.296
When working with degrees, always either use the
 symbol or write the word degree.
60 =
radians
When working with radians you may use the word
radian, the abbreviation rad, or nothing at all.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 5
More Converting of Measurements
To convert from degrees to radians, multiply by
To convert from radians to degrees, multiply by
Convert from radians to degrees:

180
180

.
Ex. 1:
5
radians
6
Ex. 2:
13
radians
8
Ex. 3:
5 radians
.
Convert from degrees to radians:
Ex. 1:
40
Ex. 2:
225
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 6
Angles in Standard Position
Quadrantal Angles and Coterminal Angles
Definition: An angle is said to be in standard
position if its vertex is at the origin of
the coordinate plane and its initial
side is on the positive x-axis.
Definition: An angle is described as quadrantal if
its terminal side is on an axis.
…, -90, 0, 90, 180, 270, 360, …


3
, 2, …
…,  , 0, , ,
2
2
2
Definition: Angles are said to be coterminal if
they have a common terminal side.
Example:
70, 430, -290
are coterminal
measurements
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 7
For an angle measurement of c degrees, c + 360n,
where n is any integer, will be a coterminal angle
measurement.
For an angle measurement c radians, c + 2n,
where n is any integer, will be a coterminal angle
measurement.
Find a coterminal angle measurement in [0, 360).
Find a coterminal angle measurement in [0, 2).
Ex. 1:
Ex. 2:
 = 1000
 = 1975
Ex. 1:
23
=
radians
3
Ex. 2:
37
=
radians
4
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 8
Arcs and Sectors of Circles
Definition: An arc is a portion of a circle between
two endpoints.
Definition: An intercepted arc is a portion of a
circle whose endpoints are points on
the rays of an angle.
Definition: A central angle of a circle is an angle
whose vertex is at the center of the
circle.
The length of an arc of a circle,
represented by s, can be
calculated using the radius r of the
circle and the measurement  in
radians of the center angle which
subtends the arc:
s = r
Definition: A sector of a circle is a region in the
interior of a circle bounded by a
central angle and the arc it subtends.
The area of a sector of a circle,
represented by As, can be
calculated using the radius r of the
circle and the measurement  in
radians of the center angle which
subtends the arc:
As = 12  r2
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 9
Calculate the length of the arc labeled s below and
the area of the sector bounded by  and s.
Ex. 1:
s
8m
Calculate the radius of the circle labeled r below
and the area of the sector bounded by  and s.
Ex. 2:
16 ft
r
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 10
Trigonometry of Right Triangles
Definition: A right triangle is a triangle with a 90
angle (right angle).
opposite leg
sin 
hypotenuse
adjacent leg
cos 
hypotenuse
Trigonometry of right triangles is based on
relationships between an acute angle and the
ratio formed by two sides of the triangle.
opposite leg
tan 
adjacent leg
adjacent leg
cot 
opposite leg
hypotenuse
sec 
adjacent leg
hypotenuse
csc 
opposite leg
With respect to the
angle  chosen in the
triangle at left, the
trigonometric ratios
of  are defined:
The sine of  is the ratio of the opposite leg to the hypotenuse.
The cosine of  is the ratio of the adjacent leg to the hypotenuse.
The tangent of  is the ratio of the opposite leg to the adjacent leg.
The cotangent of  is the ratio of the adjacent leg to the opposite leg.
The secant of  is the ratio of the hypotenuse to the adjacent leg.
The cosecant of  is the ratio of the hypotenuse to the opposite leg.
It is important to remember that the ratios are
based on the relative position of the legs of the
right triangle with respect to the angle chosen.
If  changes from one of the acute angles to the
other acute angle, the roles of opposite and
adjacent are switched.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 11
Define the trigonometric ratios of  below.
Find the third side of length using the Pythagorean
Theorem, then define the trigonometric ratios.
Ex:
Ex.:
sin 
cos 
sin 
cos 
tan 
cot 
tan 
cot 
sec 
csc 
sec 
csc 
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 12
Sketch a triangle which satisfies the given ratio &
then define the remaining trigonometric ratios.
Ex.:
2
cos 
5
Observe that a physical model of a triangle
demonstrates the consistency between the ratios
and the angles:
1 unit
sin 
tan 
cot 
sec 
csc 
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 13
Express x and y as ratios in terms of .
Ex. 1:
Express x and y as ratios in terms of .
Ex. 2:
15
12

x

x
y
y
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 14
Solving Right Triangles
Given a right triangle, if:
1. the length of two sides are known, or
2. the length of one side and the measure of
one acute angle are known,
then it is possible to find the remaining side
lengths and angle measures. A triangle is said to
be solved when all sides and angles are known.
Each trigonometric ratio is formed by one angle
and two sides. With two pieces of information, it
is possible to create an equation with only one
unknown. The inverse of a trigonometric ratio is
necessary when you are solving for an angle.
When given two sides, find the length of the third
side by the Pythagorean Theorem.
If an acute angle is known, the other acute angle
can be found using the Angle Sum Theorem.
* Angle Sum Theorem: The sum of the angle
measurements in a triangle is 180.
Sides of a triangle should always be labeled with
lower case letters. Vertices (and by extension the
angles formed at the vertices) should always be
labeled with upper case letters matching the side
opposite the angle.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 15
Solve the right triangle. Approximate as necessary
to five digits.
Ex. 1:
Solve the right triangle. Approximate as necessary
to five digits.
Ex. 2
7
52
12
8
HARTFIELD – PRECALCULUS
Solve the right triangle. Approximate as necessary
to five digits.
Ex. 3: The length of the hypotenuse is 15 units
& the larger of the two acute angles
measures 64.
UNIT 2 NOTES | PAGE 16
Sketch the triangle given in example 3.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 17
Angles of Elevation, Depression and Inclination
Definition: An angle of elevation is an angle
above horizontal that an observer
must look to see an object that is
higher than the observer.
Definition: An angle of depression is an angle
below horizontal that an observer
must look to see an object that is
lower than the observer.
Definition: An angle of inclination is an angle
formed by a line above horizontal.
We usually use an angle of inclination in the
context of an object without an observer, such as
the incline of a mountain. However this is not
always the case.
HARTFIELD – PRECALCULUS
Ex. 1: Bill is looking out the window of his third
floor apartment, 20 feet about the ground, as
illustrated at right. (Note, picture is not drawn to scale.)
A: Bill spots a $100 bill on the ground outside his
apartment. If the angle of depression is 18,
how far from Bill’s apartment building is the
money? Approximate to the nearest foot.
B: Bill sees an airplane flying in the distance.
Small planes in this area are usually flying at
10,000 feet above sea level. Bill’s apartment
building is at 1200 feet above sea level. If the
angle of elevation to see the plane is 24, by
line of sight how far away is the airplane?
Approximate to the nearest tenth of mile.
UNIT 2 NOTES | PAGE 18
HARTFIELD – PRECALCULUS
Ex. 2: George is standing near a tree that is
casting a long shadow.
A: The tree stands 40 feet high and the shadow is
100 feet long. At what angle of inclination,
with respect to the ground, is the sun based on
this shadow? Approximate to the nearest
tenth of a degree.
B: George’s eyes are 5 feet above the ground. He
spots a cardinal in the tree and the angle of
elevation for him to see the bird is 32. If
George is 30 feet from the spot beneath the
cardinal, how high up is the bird?
Approximate to the nearest tenth of a foot.
UNIT 2 NOTES | PAGE 19
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 20
Special Right Triangles
45-45-90 Triangle
30-60-90 Triangle
sin45 
sin30 
sin60 
cos45 
cos30 
cos60 
tan45 
tan30 
tan60 
cot45 
cot30 
cot60 
sec45 
sec30 
sec60 
csc45 
csc30 
csc60 
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 21
Trigonometry of Angles
By placing one of the acute angles of a triangle at
the origin in standard position, it is possible to
relate the trigonometry of right triangles to angles
in general.
Definition: Let (x, y) be a point on the terminal
side of an angle  in standard
position. Let r be the distance from
the origin to (x, y). Then:
(x, y)

We can eventually extend the definition of the
trigonometric ratios by noting that it is possible to
form a consistent definition even when the angle
is outside the interval (0, 90).

y
sin 
r
y
tan 
x
r
sec 
x
x
cos 
r
x
cot 
y
r
csc 
y
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 22
Find the trigonometric ratios of .
Ex. 1:
Find the trigonometric ratios of .
Ex. 2:
sin 
cos 
sin 
cos 
(-4, -10)
tan 
cot 
tan 
cot 
sec 
csc 
sec 
csc 
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 23
Signed values of trigonometric ratios
From the definition of each trigonometric ratio, it
is possible to know in advance whether the ratio is
going to be positive or negative.
Quadrant I
x > 0, y > 0

(0, 90) or 0, 2
sin, cos, tan, cot, sec, csc
(90, 180) or
sin, csc
cos, tan, cot, sec
 2 , 
Quadrant III
x < 0, y < 0

(180, 270) or  , 32
Quadrant IV
x > 0, y < 0
(270, 360) or

 32 ,2 
tan, cot
sin, cos, sec, csc
cos, sec
sin, tan, cot, csc
Ex. 1
sin 200
Ex. 2
sec 300
Ex. 3
tan –80
Ex. 4
cos 1180
positive

Quadrant II
x < 0, y > 0
Without determining the exact value, determine
whether the trigonometric ratio is positive or
negative.
positive
negative
positive
negative
positive
negative
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 24
Reference Angles
Definition: Let  be an angle in standard
position. Then the reference angle 
associated with  is the acute angle
formed by the terminal side of  and
the x-axis.
If  is in (0, 360) or (0, 2), and
the terminal side is in QI, then    .
the terminal side is in QII, then   180   .
    .
the terminal side is in QIII, then     180.
__

To find a reference angle  for some angle  :
   .
the terminal side is in QIV, then  360   .
__

  2   .
__

__

If  is not in (0, 360) or (0, 2), find a coterminal
angle  c that is and then apply the rules above
substituting  c for  .
HARTFIELD – PRECALCULUS
Find the reference angle  for each given  .
Ex. 1:
Ex. 2:
  290
  570
UNIT 2 NOTES | PAGE 25
Find the reference angle  for each given  .
Ex. 3:
  2390
Ex. 4:
27

5
HARTFIELD – PRECALCULUS
Reference angles and trigonometric ratios
Any trigonometric ratio involving  will have the
same absolute value as the same trigonometric
ratio involving  .
UNIT 2 NOTES | PAGE 26
Find the sine, cosine, and tangent of  .
Ex.:
Since  is acute, any trigonometric ratio involving
 will have a positive value.
Thus any trigonometric ratio of  can be defined
in terms of a trigonometric ratio of  with an
appropriate accommodation of its sign value
based on the quadrant where the terminal side of
 is found.
sin  =
cos  =
tan  =
HARTFIELD – PRECALCULUS
Rewrite each trigonometric ratio using a reference
angle and then evaluate as possible.
Ex. 1:
Ex. 2:
cos290
tan 570 
UNIT 2 NOTES | PAGE 27
Rewrite each trigonometric ratio using a reference
angle and then evaluate as possible.
Ex. 3:
sin2390
Ex. 4:
27
cos
5
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 28
Solving Oblique Triangles
Law of Sines
Defintion:
The Law of Sines is a statement of proportionality:
in any triangle each ratio formed by the sine of an
angle to the length of a side opposite the angle is
equal.
sin A sinB sinC


a
b
c
An oblique triangle is any triangle
that is not a right triangle; i.e., it does
not have a right angle.
Given a side length and two additional pieces of
information (side lengths or angle
measurements), it is possible to solve any triangle
for which a solution exists.
B
a
When given an oblique triangle with two known
angle measurements, it is possible to use the Law
of Sines to find a unique triangle solution.
c
C
A
Observation:
b
The largest angle of a triangle is
always opposite of the longest
side.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 29
Solve the triangle. Approximate as necessary to
five digits.
Ex. 1:
60
84
25
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 30
Solve the triangle. Approximate as necessary to
five digits.
Ex. 2: b = 1000
A = 22
C = 95
Sketch the triangle from example 2.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 31
Law of Cosines
When given an oblique triangle with all three
sides known or an oblique triangle where the one
known angle is between two known sides, it is
possible to use the Law of Cosines to find a unique
triangle solution.
The Law of Cosines is a set of statements
amending the Pythagorean Theorem such that it
can be applied to any triangle: the square of a side
of a triangle is equal to sum of the squares of the
other sides minus twice the product of the other
sides and the cosine of the first side.
c  a  b  2ab cos C
2
2
2
a  b  c  2bc cos A
b2  c2  a2  2ca cos B
2
B
a
2
2
c
C
A
b
After using the Law of Cosines to find an unknown
side or an unknown angle, it is possible to find the
remaining sides or angles using the Law of Sines.
The Law of Sines should never be used to find an
obtuse angle however; either use the Law of
Cosines or the Angle Sum Theorem.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 32
Solve the triangle. Approximate as necessary to
five digits.
Ex. 1:
55
10
18
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 33
Solve the triangle. Approximate as necessary to
five digits.
Ex. 2: a = 12
c = 30
B = 28
Sketch the triangle from example 2.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 34
Solve the triangle. Approximate as necessary to
five digits.
Ex. 3:
10
20
12
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 35
Solve the triangle. Approximate as necessary to
five digits.
Ex. 4: a = 20
b = 24
c = 32
Sketch the triangle from example 4.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 36
Ambiguous Case of the Law of Sines
If you are given the lengths of two sides and the
measure of angle opposite one of the sides, it is
possible for three scenarios to exist:
1. A unique solution exists for one triangle;
that is, exactly one third side length and
two additional angle measures satisfy the
given information.
2. Two parallel solutions exist, each with a
third side length and two angle measures,
that create triangles satisfying the given
information.
3. No triangle can be formed using the given
information.
The number of triangles satisfying the given
information can be determined based on what
happens when the Law of Sines is applied to find
the measure opposite of one of the side lengths:
1. If an angle measure exists and is less than
the given angle measure, exactly one
triangle satisfies the given information.
2. If an angle measure exists and is of greater
measure than the given angle, two triangles
will satisfy the given information. One
triangle will use the initially found measure
while the second triangle will use the
supplement of the found measure.
3. If no angle measure exists, then no triangle
will satisfy the given information.
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 37
Solve all possible triangles that satisfy the
information given below. Approximate as
necessary to five digits.
Ex.1: a = 16
b = 12
A = 65
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 38
Solve all possible triangles that satisfy the
information given below. Approximate as
necessary to five digits.
Ex. 2: b = 14
c = 12
C = 22
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 39
Solve all possible triangles that satisfy the
information given below. Approximate as
necessary to five digits.
Ex. 3: a = 17
c = 12
C = 79
HARTFIELD – PRECALCULUS
UNIT 2 NOTES | PAGE 40
Solve all possible triangles that satisfy the
information given below. Approximate as
necessary to five digits.
Ex. 4: a = 21
b = 25
A = 29