Download Teacher-directed Lesson Plan – Exploring the Laws of Sines and

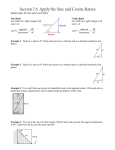
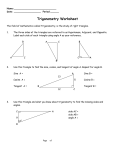
GeoGebra Lesson
1
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
Shawn Urban
of 12
Teacher-directed Lesson Plan – Exploring the Laws of Sines and Cosines
Purpose and Objectives
Jump to Lesson (p. 5)
Students will …
 comprehend, concretely illustrate and explain the properties of the Sine and Cosine Laws
and their relation to triangle properties and Pythagoras Theorem
 actively manipulate triangles and see the visual and algebraic effects of this manipulation
 demonstrate their understanding of the Sine and Cosine Laws
(This lesson does not include problem solving involving the Sine and Cosine Laws.)
Mathematical Outcome
(Alberta Learning 2002a, p. 14, Alberta Learning 2002b, p. 14)
Grade 10 Trigonometry Specific Outcome (P10Trig6.3, A10Trig6.3)
Students will apply the Sine and Cosine Laws, excluding the ambiguous case, to solve
problems.
(Alberta Education 2008, p. 33, 61)
Grade 11 Trigonometry Specific Outcome (20-1.T3)
Solve problems, using the cosine law and sine law, including the ambiguous case.
Grade 11 Geometry Specific Outcome (20-2.G3)
Solve problems that involve the cosine law and the sine law, excluding the ambiguous
case.
Mathematical Processes (Alberta Learning 1996, p. 4-9)
Students will visualize and make connections, using technology, to solve, reason and learn
what the Sine and Cosine Laws represent and how and why they work.
Mathematical Understanding (Alberta Learning 2002c, p. 2)
Students will develop a conceptual understanding of the Sine and Cosine Laws, rather than
a procedural or problem solving understanding of them.
Nature of Mathematics (Alberta Learning 1996, p. 9-11)
Students will develop an intuitive feel about change, constancy, relationship and shape as
it applies to triangles and the Sine and Cosine Laws.
Performance Standards (Alberta Learning 2002c, p. 138)
Determine any side or angle of a triangle using the either the Sine Law or the Cosine Law,
whether or not you are given a diagram and/or formula to work from.
ICT Outcomes (Alberta Education 1998b, p. 5, 14-15)
C6. Students will use technology to investigate and/or solve problems.
4.4. Generate new understanding of problematic situations by using some form of
technology to facilitate the process.
C7. Students will use electronic research techniques to construct personal knowledge and
meaning.
4.2. Analyze and synthesize information to determine patterns and links among ideas.
Nature of and Rationale for This Lesson
 lesson goal: engage students in the exploration of the Sine and Cosine Laws through
guiding questions and tactic and visual exploration via associated triangle manipulation
o it has been my experience through teaching and tutoring that students memorize the sine
ratios and cosine formulae without a true understanding about how the Sine and Cosine
GeoGebra Lesson
2
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
Shawn Urban
of 12
Laws influence and describe triangle shape (Urban 2005); most of these students use the
Laws without understanding them and when to use them (they develop procedures for
choosing based on trial and error); they lack the appreciation of the mathematics
underlying the Laws (Pimm 2005)
o this restricts the students’ ability to learn the Laws beyond the knowledge (memorizing
of the formulae and their components) level of Bloom’s taxonomy (Noble 2004)
o these students end up memorizing four to six formulae too similar to differentiate and
use strategically; the students typically do not understand that these formulae are
manifestations of two Laws and not separate entities; they have no base to choose one
formula version over another, leading to confusion and frustration with trigonometry
o this lesson is based on several manipulative demonstrations I developed and found
successful in enabling insightful high-level understanding of the Sine and Cosine Laws
 the lesson is related to:
o trigonometry and the properties of triangles
o the derivation and application (in solving problems) of the Sine and Cosine Laws
 the relevant application of the Sine and Cosine Laws to solve problems is mandated
in A10Trig6.3, P10Trig6.3, 20-1.T3 and 20-2.G3, and detailed in the performance
standards of A- and P10Trig6.3 (Alberta Learning 2002c, p. 138)
 the derivation of the Laws and problem solving using the Laws are not addressed
here; student attention is focussed on the concepts the Laws are based on and on the
related properties of triangles and the Pythagoras Theorem (Wiggins and McTighe
1998)
 GeoGebra and Geometer’s Sketchpad
o equivalent GeoGebra and Sketchpad documents were designed as a tool (JohnstonWilder and Pimm 2005) to demonstrate dynamically the relationship between the
properties of triangles and the component parts of the sine ratios and cosine formulae
o the tool consists of two autonomous triangles each constructed by connecting three free
(floating or unanchored) points; the points (vertices) are unanchored to maximize
manipulation possibilities of the triangles
o the student or demonstrator grabs and drags a vertex or edge to change the shape of
either triangle
o the edge lengths and angle measurements are dynamically quantified in response to this
manipulation
o the sine or cosine formulae (depending on which triangle is manipulated) are updated on
the screen as the measurements change
o the top (Sketchpad) or left (GeoGebra) triangle demonstrates the connection between
triangle shape and the sine ratios
o the bottom or right triangle does this with reference to the cosine formulae
o students see, among other things:
 the equivalence (in value) of the sine ratios of the three edge-angle pairs of the sine
triangle as the sine triangle is manipulated (this is the Sine Law)
 the relationship of the Pythagoras Theorem and the Cosine Law and the influence of
the correction term (-2nm(cosP)) in the cosine formulae as the cosine triangle is
manipulated
 the equivalence (in function) of the cosine formulae; that is, though which edges and
angles referred to change from formula to formula, the difference between the
GeoGebra Lesson
3
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
Shawn Urban
of 12
formulae is one of orientation only (they are versions of the same formula doing the
same thing just from different orientations, much like the sine ratios)
o the demonstrator also points out, through leading questions and manipulations, less
obvious, more interactive features of triangle properties during the demonstration,
deepening student understanding of the mathematics underlying the Sine and Cosine
Laws
o from the students move beyond memorizing formulae to gaining enough understanding
and insight of triangle dynamics to “derive” the Sine and Cosine Laws and explain why
and how they work
o objects and texts in the GeoGebra and Sketchpad documents are boxed and color coded
to direct student attention, and aid in communication
o students are interactively engaged through inquiry during the demonstration; they also
have opportunity to inquire, respond to inquiry and demonstrate manipulations
o the tool builds upon prior concepts, such as the derivation of the Pythagoras Theorem
and the Sine and Cosine Laws; the main focus of this lesson is to explain concretely and
visually what these Laws and the Theorem mean geometrically
o the tool also sets the stage for using the Laws to solve problems (outcomes above)
o the tool provides active learning in several multiple intelligences (Mackrell and
Johnston-Wilder 2005), particularly visual, aural, tactical, interpersonal, intrapersonal
and logical, at several Bloom hierarchies (Noble 2004)
o the tool enriches student experience by encouraging the student to directly explore the
concepts and pursue the mathematics underlying the Sine and Cosine Laws, by enabling
a multi-way interaction between the demonstrator, the tool, and the ears, eyes, hands,
mind and imagination of the student, and by enabling interactive demonstrator-student
inquiry and static and dynamic scrutiny and contemplation of manipulation results
(Mackrell and Johnston-Wilder 2005)
o the tool is simple and lacks technological flourish emphasizing active multifaceted
engagement with the content and mathematics of the lesson over passive multimedia
entertainment with the technology (Carbonaro 2003)
 the lesson can typically be completed in one 45 minute period
o half of this time (20 minutes) is spent on demonstrating the geometric properties of the
Sine and Cosine Laws through question-driven inquiry and exploration; the teacher can
do this or the students can work in small groups; students are engaged by answering and
asking questions, walking through the concepts and properties underlying the Sine and
Cosine Laws, and filling out a question sheet
o the demonstration dominates since it moulds the concepts, the embodiment of the lesson
o for five to ten minutes at the beginning of the class students are allowed to play with the
tool on their computers; the demonstrator can guide them through grabbing and
dragging a vertex, followed by an edge, while handing out question sheets; students
have the opportunity to feel what the tool is doing and what changes and remains
constant as they move things about; they also get a chance to mess things up, readying
them for guidance (Phillips 1998) (the document must be read-only); this play can be
enriched by asking the students to list as many relevant things they notice as they can
(shades of science, free inductive; question sheets: guided inductive and deductive)
o for the last 15 minutes students play with the tool, complete their question sheets,
answer their take-home assignment and ask questions
GeoGebra Lesson
4
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
Shawn Urban
of 12
o the independent, task-directed exploration enables students to test the concepts in a
focussed manner, so giving the students ownership of the concepts (Pimm 2005)
o the play before and after the demonstration resonate against each other, giving students
a concrete sense of progress, accomplishment, success and learning (Phillips 1998)
 students will be assessed based on the quality of their responses on the question sheet and
their take-home assignment
o the question sheet will have on it the same questions asked by the demonstrator during
the demonstration; the take-home assignment will be a summarization of the Sine and
Cosine Laws and their properties (both provided following the lesson plan)
o this assessment strategy places emphasis on the concepts and mathematics underlying
the Sine and Cosine Laws and enables the student to demonstrate his or her level of
understanding of these Laws
o it also compels student responsibility for paying attention and asking and answering
questions during the demonstration; this should reduce off-task playing with the tool
during the demonstration
Mastered Prerequisites
 Students should be capable of performing simple computer-interfacing activities, such as
selecting (clicking on an object) and dragging (moving the cursor with the selection button
pressed down)
 Students should recognize the Pythagoras Theorem and the Sine and Cosine Laws and
possibly be familiar with their derivation (review the Pythagoras.gsp and Law of
Cosines.gsp files in the Sketchpad Homepage sample sketches folder)
 Aside: When rotated so its white squares are aligned horizontally and vertically and the
side labelled c is under the object, the Leonardo da Pythagoras object in Pythagoras.gsp
can be translated into the Law of Cosines.gsp object when this object’s point C is dragged
onto the LoC object’s bottom edge; the only difference between the two objects would be
two triangles missing from the Leonardo da Pythagoras object (with these two triangles,
the Leonardo da Pythagoras proof would still hold and in fact would represent the left
object of Behold Pythagoras in Pythogoras.gsp when its point D is dragged toward the left
until its green center square touches the corners of the outer square)
Extensions
 This tool and this lesson can be revisited (in or before, as a precursor, Grade 11 or 12) or
enriched to teach the generalized form of Thale’s Theorem in circle geometry (equal angles
on the circumference of a circle are subtended by the same chord); this would relate the
Pythagoras and Thale’s Theorems and the Sine and Cosine Laws in a different light (it
could for instance provide a different visual take on the correction term in the Law of
Cosines and another proof of this Law); the triangles would need to be reconstructed so all
vertices are bound to a circle; a dynamic right triangle can be constructed when the chord
is fixed as the diameter of the circle (by also fixing its endpoints to a line to which the
origin of the circle is fixed)
GeoGebra Lesson
5
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
Shawn Urban
of 12
Lesson
Materials and Learning Resources
- computers with Geometer’s Sketchpad or access to GeoGebra on the Web;
- file triglaws.gsp or triglaws.ggb or the html shell (automatically read-only) of this (html
shells of both available at http://www.ualberta.ca/~urban/);
- pencils and erasers, or pens;
- paper;
- photocopied question sheet (one per student);
- the take-home question
Starter (5 – 10 min)
- allow students to fool around with the graphing tool; let them “drown” (Phillips 1998);
possibly formatively assess play; direct them to drag any triangle vertex and edge about; ask
them to list as many things (approximately, at least ten) they notice about each of the
manipulations (triangles) as they can
- purpose: get students used to what the tool does and what manipulation of the triangles does;
some might focus on what changes and what remains constant
- hand out question sheets
GeoGebra Lesson
6
Demonstration (20 min)
Query
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
Shawn Urban
of 12
students follow along with their question sheets
Action
Law of Sines
What happens to the numbers in the
- Select and drag each vertex one after another.
sine formulae when we move one of
- Pause periodically to let the measurements and
the sine triangle’s vertices about?
calculations in the formulae settle.
- Repeat with each edge.
- Students should see (van Hiele level 2, Mackrell and
Johnston-Wilder 2005):
- change in the ratios
One of its sides?
- equivalence in the ratios
- change in the lengths, angles and sines
- Students should conclude: the sine-angle – edge length
ratios equal each other regardless of the position of the
moved vertex / edge (true for all triangles)
Are there any instances where this
- Challenge students to try to break this speculation
observation is broken?
- on their own computers
- using the projected version
- For instance, what happens if they change the edge
lengths, but not the angle widths? If they change the
angles widths, but not the edge? (in both cases, arc in a
circle, focus on what remains constant)
How can we simulate opening
- Select a vertex and drag it
(widening) and closing (narrowing)
- Focus student attention on each of the other angles one
of one of the angles?
after the other
- Ensure the students see the angle opening and closing
What happens to the length of a side - Focus their attention on the length of the side opposite
when we open the angle opposite the
this angle
side?
- Ensure they see that the length of the side and the
width (openness) of the angle are synchronized
When we close the angle?
- Reverse their focus by stressing the edge length and
ensuring they see that the angle width (openness)
Does it matter whether the angle is
changes with it
right, acute, obtuse or straight?
- Repeat, selecting and dragging the other vertices if
needed
What happens to an angle when we
- Clarify the concept by hinging your hands at the base of
shorten the side opposite it?
your palms and opening and closing them or by
opening and closing two “hinged” (at a common
When we lengthen the side?
corner) sheets of paper on an overhead
- Enrich by relating changes (length of all edges, width
of all angles) while dragging the vertex
- all this: van Hiele level 3 (ref ibid)
What happens if a side approaches
- Select an edge and drag it (approach, retreat and brush
its opposite angle?
about)
- Repeat, selecting and dragging the other edges if
Retreats from its opposite angle?
needed
GeoGebra Lesson
7
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
Enrichment: What happens when an
angle’s width (openness) is kept
constant as you drag its vertex?
What happens when a side’s length
is kept constant as you drag its
endpoint?
Review: What information do you
need to determine a Sine Law ratio?
What information do you need to
answer trigonometric questions
involving the Sine Law?
For what types of analysis (SAA,
SSS, etc.) can you use the Sine Law
unambiguously?
Shawn Urban
of 12
- Constant angle width: Thale’s Theorem
- One edge (the chord) remains the same length and its
opposite angle remains the same width; the others
change; the sine ratios remain constant; the vertex
traces a circle
- Constant edge length: circle radius
- One edge (the radius) remains the same length; all
other measurements change; treat as an unanchored
vertex (or edge) except that it traces a circle (or disc)
- Answers:
- The length of an edge and the width of its opposite
angle
- Two edge – opposite angle pairs (all values except
one)
- SAA, ASA, SSA (have students draw and explain
why they know these work, AAA and SAS don’t and
SSS is ambiguous)
Retreats from its opposite angle?
Law of Cosines
- Select and drag each vertex one after another.
- Repeat with each edge.
- Each widens or narrows as the other widens or narrows
(much like the edge – opposite angle pairs of the Sine
Law)
- Select and drag each vertex one after another.
- Pause periodically to let the measurements and
calculations in the formulae settle.
- Repeat with each edge.
- Students should see (van Hiele level 2, ref ibid):
- squares of side lengths and Cosine Law functions
change
- p2s and Cosine Law functions are equal
- Students should conclude: the square of each side
length equals the corresponding Cosine Law function
Does it matter whether the angle is
right, acute, obtuse or straight?
Does this observation hold for all
three formulae?
- Continue the demonstration as above.
- The three formulae differ only in their orientations.
How are opposite sides and opposite
angles related?
What happens to the numbers in the
cosine formulae when we slide one
of the cosine triangle’s vertices?
One of its sides?
What happens if a side approaches
its opposite angle?
What is the difference between the
three formulae?
Are there any instances where this
observation is broken?
- Challenge students to try to break this speculation
- on their own computers
- using the projected version
GeoGebra Lesson
8
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
How are the Pythagoras Theorem
and the Law of Cosines related?
Different?
Explain how the correction term,
-2*m*n*cos(P), works.
What is the relationship of the sides
and the angle in the correction
term?
What is the relationship of the sides
in the correction term and the “legsides” of the corresponding
Pythagoras Theorem?
What is the relationship of the
“slope-side” and the angle?
Is this side always longer than the
other two?
Enrichment: What happens when an
angle’s width (openness) is kept
constant as you drag its vertex?
What happens when a side’s length
is kept constant as you drag its
endpoint?
Review: What information do you
need to answer trigonometric
questions involving the Cosine Law?
Shawn Urban
of 12
- What happens if angle width equals 0o, 45o, 90o, 135o
and 180o?
- Ensure the students see that the correction term
accounts for the width of the angle P; that the
Pythagoras Theorem is the Law of Cosines for P = 90o
- Clarify the concept on an overhead by opening and
closing two “hinged” sheets of paper superimposing a
transparency of a right angle (the hinge and the right
vertex should superimpose, as should one of the legs of
the each angle; colored transparency sheets work best)
- The value of the correction term (including the
subtraction sign) increases or decreases as the
corresponding angle increases or decreases
- SAS
- The edges in the correction term and the “leg-edges”
are the same; note how lengths change
- Treating the triangle as a stair, where the leg-edges are
the rise and run of the stair, the “slope-edge” is opposite
the angle; the slope-edge need not be longer than each
of the leg-edges
- Constant angle width: Thale’s Theorem
- One edge (the chord) remains the same length and its
opposite angle remains the same width; the others
change; the Cosine Law still holds since both the
Pythagoras portion and the correction term involve
the other edges; the vertex traces a circle
- Constant edge length: circle radius
- One edge (the radius) remains the same length; all
other measurements change; treat as an unanchored
vertex (or edge) except that it traces a circle (or disc)
- Answers:
- SAS or SSS
- SAS, SSS (have students draw and explain why they
know these work, AAA, ASA, SAA don’t and SSA
is ambiguous)
For what types of analysis (SAA,
SSS, etc.) can you use the Cosine
Law unambiguously?
Closure (15 min)
- enable and encourage students to:
- fix, complete and revisit questions in the question sheet
- work on their take-home assignment
- ask questions
- discuss what they learned
- play with the tool given the informed context of the demonstration
GeoGebra Lesson
9
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
Shawn Urban
of 12
Hand-out Question Sheet
LAW OF SINES (top or left triangle) – 25 + 10 bonus
What happens to the numbers in the sine formulae when we move one of the sine triangle’s
vertices about? (2)
One of its sides? (2)
Are there any instances where this observation is broken? (2, with explanation)
How can we simulate opening (widening) and closing (narrowing) of one of the angles? (1)
What happens to the length of a side when we open the angle opposite the side? (1)
When we close the angle? (1)
Does it matter whether the angle is right, acute, obtuse or straight? (1)
What happens to an angle when we shorten the side opposite it? (1)
When we lengthen the side? (1)
What happens if a side approaches its opposite angle? (1)
Retreats from its opposite angle? (1)
Enrichment:
What happens when an angle’s width (openness) is kept constant as you drag its vertex? (5
bonus)
What happens when a side’s length is kept constant as you drag its endpoint? (5 bonus)
Review:
What information do you need to determine a Sine Law ratio? (2)
GeoGebra Lesson
10
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
Shawn Urban
of 12
What information do you need to answer trigonometric questions involving the Sine Law? (3)
For what types of analysis (SAA, SSS, etc.) can you use the Sine Law unambiguously? (6, with
explanation)
LAW OF COSINES (bottom or right triangle) – 34 + 10 bonus
How are opposite sides and opposite angles related? (2)
What happens to the numbers in the cosine formulae when we slide one of the cosine triangle’s
vertices about? (3)
One of its sides? (3)
What happens if a side approaches its opposite angle? (1)
Retreats from its opposite angle? (1)
Does it matter whether the angle is right, acute, obtuse or straight? (1)
Do the numbers in the cosine formulae behave similarly for all three formulae? (2, with
explanation)
What is the difference between the three formulae? (1)
Are there any instances where this observed behavior is broken? (2, with explanation)
How are the Pythagoras Theorem and the Law of Cosines related? (1)
How are they different? (1)
Explain how the correction term, -2*m*n*cos(P), works. (2)
GeoGebra Lesson
11
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
Shawn Urban
of 12
What is the relationship of the sides and the angle in the correction term? (1)
What is the relationship of the sides in the correction term and the “leg-sides” of the
corresponding Pythagoras Theorem? (1)
What is the relationship of the “slope-side” and the angle? (1)
Is this side always longer than the other two? (2, with explanation)
Enrichment:
What happens when an angle’s width (openness) is kept constant as you drag its vertex? (6
bonus)
What happens when a side’s length is kept constant as you drag its endpoint? (4 bonus)
Review:
What information do you need to answer trigonometric questions involving the Cosine Law? (3)
For what types of analysis (SAA, SSS, etc.) can you use the Cosine Law unambiguously? (6, with
explanation)
Take-home Assignment
Describe and explain the Sine and Cosine Laws and their relationship to triangle properties, the
Pythagoras Theorem and problem solving involving these Laws. Use illustrations, words and
formulae to clarify your explanation. In what situations can you use each Law to effectively
solve problems? (20)
GeoGebra Lesson
12
Exploring the Laws of Sines and Cosines
January 17, 2010 (update)
Shawn Urban
of 12
References
Alberta Education. (2008). Mathematics Grades 10–12 Program of Studies with Achievement
Indicators. Edmonton, Alberta: Crown in Right of Alberta. Pages as cited.
Alberta Education. (1998b). Illustrative Examples to Accompany Information and
Communications Technology Interim Program of Studies: Grade 10 to Grade 12.
Edmonton, Alberta: Crown in Right of Alberta. Pages as cited.
Alberta Learning. (2002a). Pure Mathematics 10-20-30 (Senior High). Edmonton, Alberta:
Crown in Right of Alberta. Pages as cited.
Alberta Learning. (2002b). Applied Mathematics 10-20-30 (Senior High). Edmonton, Alberta:
Crown in Right of Alberta. Pages as cited.
Alberta Learning. (2002c). Outcomes with Assessment Standards for Pure Mathematics 10.
Edmonton, Alberta: Crown in Right of Alberta. Pages as cited.
Alberta Learning. (1996). Alberta Program of Studies for K-9 Mathematics, 1996. Edmonton,
Alberta: Crown in Right of Alberta. Pages as cited.
Carbonaro, Michael. (2003). Discussions in EDIT 202: Technology Tools for Teaching and
Learning. Personal Communication.
Johnston-Wilder, Sue and Pimm, David. (2005). Some technological tools of the mathematics
teacher’s trade. In Teaching Secondary Mathematics with ICT. (Eds). Johnston-Wilder,
Sue and Pimm, David. Maidenhead, England: Open University Press. p. 18.
Mackrell, Kate and Johnston-Wilder, Peter. (2005). Thinking geometrically: Dynamic
imagery. In Teaching Secondary Mathematics with ICT. (Eds). Johnston-Wilder, Sue and
Pimm, David. Maidenhead, England: Open University Press. p. 81-100.
Noble, Toni. (2004). Integrating the Revised Bloom’s Taxonomy with Multiple Intelligence:
A planning tool for curriculum differentiation. Teachers College Record 106 (1): 193-211.
Phillips, Hugh. (1998). Floundering before teaching: Paddling in deep water. Designing and
Delivering Dynamic Workshops. Edmonton, Alberta: HP Training Works, Inc. Personal
Communication.
Pimm, David. (2005). Discussions in EDSE 540: Mathematics Education: Exploring Tasks,
Curricula and Programs. Personal Communication.
Wiggins, Grant and McTighe, Jay. (1998). Understanding by Design. Alexandria, Virginia:
Association for Supervision and Curriculum Development.
Urban, Shawn. (2005). Insight and practicalities: On teaching and tutoring sines and cosines
at Sylvan Learning Center in Sherwood Park. Personal Communication.