Download 2.1 Patterns and Inductive Reasoning Inductive Reasoning

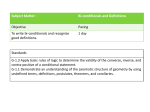
2.1 Patterns and Inductive Reasoning
Inductive Reasoning: Reasoning based on observed patterns.
Ex: Describe a visual pattern
a. Describe how to sketch the fourth figure in the pattern. Then sketch the fourth figure.
Solution
Each rectangle is divided into _two more_ regions than the previous rectangle. The bottom left region is shaded.
b. Sketch the fifth figure in the pattern.
Ex: Describe the number pattern
Describe the pattern in the numbers –1, –4, –16, –64, …. Write the next three numbers in the pattern.
(Note the three dots (…) tell you that the pattern continues.)
Notice that each number in the pattern is _four_ times the previous number.
The next three numbers are _–256, –1024, and –4096
Conjecture: A conclusion that you reached using inductive reasoning.
Example: Make a conjecture about the sum of two even numbers.
2+4 = 6, 6 + 10 = 16, 34+ 10 = 44
The sum is an even number.
Example: What conjecture can you make about the sum of the first 30 even numbers?
The sum of the first 30 even numbers is 30 · 31 = 930.
Example: Use inductive reasoning to predict the average salary of an NFL player 5 years out.
About $1400 thousand.
Counterexample: An example that shows the conjecture is incorrect.
Example: Find a counterexample for the conjecture.
Conjecture: The difference of any two numbers is always smaller than the larger number.
Counterexample:
8 – (–4) = _12_
Because _12_ > _8_, a counterexample exists. The conjecture is false.
2.2 Conditional Statements
Conditional statement: An if-then statement with a hypothesis and a conclusuion.
Ex: Rewrite the conditional statement in if-then form:
a. All whales are mammals. (If an animal is a whale, then it is a mammal.)
b. Three points are collinear if there is a line containing them. (If there is a line containing
three points, then the points are collinear.)
c. Vertical angles share a vertex. (If two angles are vertical, then they share a vertex.)
Verifying Conditional Statements
Conditional statements can be true or false.
To show a conditional statement is true: Prove that the conclusion is true every time the hypothesis is true
To show a conditional statement is false: Find one counterexample
Converse of a conditional statement – The hypothesis and the conclusion are switched
Ex: Conditional statement: If I am in this class, then I go to Dowling. (True)
Converse: If I go to Dowling, then I am in this class. (False)
2.3 Biconditionals and Definitions
Biconditional statements – When a conditional statement and its converse are both true, we can write the
statement with “if and only if”
Ex: Conditional Statement: If two lines intersect to form a right angle, then they are perpendicular. (True)
Converse Statement: If two lines are perpendicular, then they intersect to form a right angle. (True)
Biconditional: Two lines are perpendicular if and only if they intersect to form a right angle.
Ex: Write the definition of supplementary angles as a biconditional:
Definition: If the sum of the measures of two angles is 180°, then the angles are supplementary.(True)
Converse: If two angles are supplementary, then the sum of their measures is 180°.(True)
Biconditional: The sum of the measures of two angles is 180° if and only if the angles are supplementary.
Identifying the conditionals in a biconditional: Write as two conditionals that are converses.
Ex.
Biconditional: Two lines are perpendicular if and only if they intersect to form four right angles.
1. If two lines are perpendicular, then they intersect to form four right angles.
2. If two lines intersect to form four right angles, then the lines are perpendicular.
Writing Definitions as a biconditional:
Definition needs to be reversible (converse is true).
Ex: Definition of quadrilateral: A quadrilateral is a polygon with four sides.
Conditional: If a figure is a quadrilateral, then it is a polygon with 4 sides. (True)
Converse: If a figure has 4 sides, then it is a quadrilateral. (True)
Biconditional: A figure is a quadrilateral if and only if it is a polygon with 4 sides.
2.5 Reasoning in Algebra and Geometry
Ex. Solve and justify each step.
3x + 6 + 2 = -4x – 34 (Given)
3x + 8 = -4x – 34
(Combine like terms)
7x + 8 = -34
(Addition Property of Equality)
7x = -42
(Subtraction Property of Equality)
X = -6
(Division Property of Equality)
Ex. Solve and justify each step.
60 = -3(8x – 4)
(Given)
60 = -24x + 12
(Distributive Property)
48 = -24x
(Subtraction Property of Equality)
X = -2
(Division Property of Equality)
Ex. What property is used?
1. m<X = m<Y
m<Y = m<X
Symmetric Property of Equality
̅̅̅̅, 𝑂𝑃
̅̅̅̅ ≅ 𝑄𝑅
̅̅̅̅ , 𝑡ℎ𝑒𝑛 𝑀𝑁
̅̅̅̅
̅̅̅̅̅ ≅ 𝑂𝑃
̅̅̅̅̅ ≅ 𝑄𝑅
2. 𝑀𝑁
3. XY = XY
Transitive Property of Congruence
Reflexive Property of Equality
Proof: A logical argument of definitions and statements that shows why a conjecture is true.
1.
2.
3.
4.
Statements
m < 1 = m <3
m<2 = m<2
m<1 + m<2 = m<3 + m<2
m <AEC = m<DEB
Reasons
1. Given
2. Reflexive Property of Equality
3. Addition Property of Equality
4. Substitution Property
1.
2.
3.
4.
5.
6.
Statements
<CDE and <EDF are supplementary
m<CDE + m<EDF = 180
x + 3x + 20 = 180
4x + 20 = 180
4x =160
x = 40
1.
2.
3.
4.
5.
6.
Reasons
Given
Definition of Supplementary
Substitution
Combine like terms
Subtraction Property of Equality
Division Property of Equality
(Congruent segments have
equal lengths)
2.6 Proving Angles Congruent
Vertical Angles Theorem: Vertical Angle are congruent.
< 1 ≅ < 3, < 2 ≅ < 4
Statements
<2 ≅ <3
<2 ≅ <6
<3 ≅ <6
Ex: Find m<AEB.
4x – 18 = 3x + 4
X = 22
M<AEB = 4(22) – 18
= 70
Reasons
Given
Vertical Angles Theorem
Transitive Property of Congruence