Download The world through a spinning window

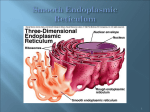
10.1117/2.1200710.0887
The world through a spinning
window
Jonathan Leach, Amanda Wright, Joerg Goette, John Girkin,
Les Allen, Steve Barnett, and Miles Padgett
Researchers revisit experiments begun over a century ago concerning
the interplay between light and matter.
In 1818, the French physicist Augustin-Jean Fresnel predicted
that light passing through a moving medium would be
dragged sideways, a phenomenon he called ether drag. Although the effect may not intrude on our everyday lives,
it is of fundamental scientific interest. A century and a
half later, R. V. Jones, an English physicist working at
the University of Aberdeen in Scotland, set out to prove
ether drag experimentally and to measure it for the first
time.1, 2
Jones showed that a beam of light falling normally (i.e., incident) on a block of glass moving with velocity v and length L
was laterally displaced by a small amount, ∆beam , given by
vL n − n−1
(1)
∆beam =
c
where n is the refractive index of glass and c is the speed of light.
In addition to demonstrating the ether drag, Jones found that
when transmitted along the rotation axis, the linear polarization state (the orientation of the electric field vector) was rotated
through a small angle ∆θpol 3
ΩL ∆θpol =
n − n−1
(2)
c
where Ω is the angular velocity or rotation rate of the medium.
These experiments were supported by the theoretical analysis of
M. A. Player4, 5 and G. L. Rogers.6 The phenomenon has come to
be known as the mechanical Faraday effect, owing to its similarities to Michael Faraday’s finding in 1845 regarding the effect of
a magnetic field on light.7
We became interested in the problem while working on the
Abraham–Minkowski controversy, a 100-year-old debate about
the momentum of light inside dielectric materials such as glass.
But our focus was angular momentum as opposed to linear momentum, so we were concerned with rotation.
Figure 1. The transverse photon drag phenomenon as interpreted in
both (a) the lab frame and (b) that of the moving medium. In the lab
frame, the glass moves with a velocity v, and the light enters perpendicular to the surface. In the rest frame of the glass, the light moves
with a velocity v and enters the glass at an angle β =v/c, where c is the
speed of light.
Due to the equivalence of spin and orbital angular
momentum,8 the spinning medium should rotate not just the
phase of a transmitted light beam but also the polarization
state.9, 10 The phase shift acquired by a transmitted light beam
in fact manifests itself as an image rotation given by
∆θimage =
Ω L n − n−1 .
c
(3)
In these phenomena, total displacement (see Equation 1) and
total rotation (see Equation 3) represent the contribution from
two separate terms. One is associated with the optical delay of
light passing through a dielectric medium, ∆delay ∝ n − 1. The
other has to do with refraction of the light in the rest frame—
Continued on next page
10.1117/2.1200710.0887 Page 2/3
i.e., in which a particular object or system is not moving—of the
medium, ∆refrac ∝ 1 − n−1 (see Figure 1). Note that in the rest
frame the light is no longer at normal incidence but is inclined at
an angle given by β = v/c.
Our initial approach to measuring this effect was to rotate a
20cm glass bar at approximately 200Hz using a geared system
built on a washing machine motor. The predicted value for the
image rotation is on the order of a few microradians. The noise in
the current system, however, is larger than the predicted value,
and we are currently working on alternative schemes.
The second approach was to switch to a case where we rotate or translate the light rather than the dielectric medium (see
Figure 2). By interfering two light beams with a well-defined
frequency shift, δν, between them, we can produce moving
fringes—that is, the light patterns generated when two coherent
beams combine—with a well-defined velocity. Alternatively, by
interfering helically phased beams, the resulting pattern is that
of a petal. If the beams differ in frequency, the petal spins with an
angular velocity Ω = δν /2l, where l is the orbital angular momentum per photon in units of h̄ (Planck’s constant). This second
approach has the following advantage over the first: it is possible to frequency-shift light beams by tens of megahertz such that
the angular velocity of the interference pattern is approximately
1 million orders of magnitude larger than that achieved with a
rotating glass bar.
This result raises an obvious question about whether the two
cases—the first, where the glass is moving, and the second,
Figure 2. Two interference patterns are generated and incident on a
ground-glass screen. The screen is imaged onto the camera such that
one of these interference patterns is captured through the 20cm-long
glass bar, the other through free space.
Figure 3. The measured displacement of the nonlocalized interference
fringes as a function of their translational velocity. The angle of the
medium is adjusted to account for the angle of incidence of the light.
where the image is moving—are equivalent, or whether there
are subtle differences between them. It turns out that for rotating or translating images passed through a stationary dielectric
medium, the measured rotation or displacement of the image
scales as n − 1, not as n − 1/n as Equations 1 and 3 predict. Only
∆delay contributes to the measured effect. The ∆refrac term is not
present.
When considering each frame of reference for this circumstance, it becomes apparent that the light always enters the
medium at normal incidence. This is in contrast to the rotating
or translating example, where the light is incident at an angle
of β = v/c in the rest frame of the glass. In order to recover
∆refrac in the instance of the translating image, the medium must
be tilted such that the angle of incidence is matched to β = v/c.
Once this criterion is met, the measured delay is indeed the sum
of ∆delay and ∆refrac (see Figure 3). Unfortunately, extension of
the experiment to include the refractive terms is not so straightforward. The end faces of the glass bar would need to behave
like an axicon (i.e., a cone), which is not possible given their flatness.
Conclusions
Beyond confirming the work of Jones, our experiments help to
reveal the subtle relationships between light and moving media.
However surprising it may seem, one consequence of these interactions is that the world viewed through a spinning window
is indeed rotated.
Continued on next page
10.1117/2.1200710.0887 Page 3/3
Author Information
Jonathan Leach, Joerg Goette, Les Allen, and Miles Padgett
University of Glasgow
Glasgow, United Kingdom
Jonathan Leach is a research assistant at the University of Glasgow. Having completed his PhD on optical vortices, he is currently studying the effect of moving media on the properties of
light.
Amanda Wright, John Girkin, and Steve Barnett
University of Strathclyde
Glasgow, United Kingdom
References
1. R. V. Jones, Fresnel drag in a transversly moving medium, Proc. R. Soc. London, Ser.
A 328, p. 337, 1972.
2. R. V. Jones, Ether drag in a transversely moving medium, Proc. R. Soc. London, Ser.
A 345, p. 351, 1975.
3. R. V. Jones, Rotary ether drag, Proc. R. Soc. London, Ser. A 349, p. 423, 1976.
4. M. A. Player, Dispersion and tranverse aether drag, Proc. R. Soc. London, Ser. A
345, p. 343, 1975.
5. M. A. Player, Dragging of plane of polarization of light propagating in a rotating
medium, Proc. R. Soc. London, Ser. A 349, p. 441, 1976.
6. G. L. Rogers, Presence of a dispersion term in transverse fresnelether-drag experiment,
Proc. R. Soc. London, Ser. A 345, pp. 345–349, 1975.
7. G. Nienhuis, J. P. Woerdman, and I. Kuscer, Magnetic and mechanical Faraday effects, Phys. Rev. A 46, p. 7079, 1992.
8. M. J. Padgett and L. Allen, Light with a twist in its tail, Contemp. Phys. 41,
pp. 275–285, 2000.
9. M. Padgett, G. Whyte, J. Girkin, A. Wright, L. Allen, P. Öhberg, and S. M. Barnett,
Polarization and image rotation induced by a rotating dielectric rod: an optical angular
momentum interpretation, Opt. Lett. 31, p. 220, 2006.
10. J. B. Götte, S. M. Barnett, and M. Padgett, On the dragging of light by a rotating
medium, Proc. R. Soc. London, Ser. A 463, pp. 2185–2194, 2007.
c 2007 SPIE