Download Date

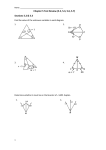
Name _______________________________________ Date ___________________ Class __________________
Indirect Proof and Inequalities in One Triangle
A. Consider the statement “Two acute angles do not form a linear pair.”
Steps
1. Identify the conjecture to be
proven.
Given:
Prove:
2. Assume the opposite of the
conclusion is true.
3. Use direct reasoning to show
that the assumption leads to a
contradiction.
4. Conclude that the assumption is
false and hence that the original
conjecture must be true.
B. Use the following statement for Exercises 1–4.
An obtuse triangle cannot have a right angle.
1. Given: ____________________________________________
Prove: ______________________________________
2. To write this indirect proof, what should you assume?
_________________________________________________________________________
3. Use direct reasoning to arrive at a contradiction.
4. What can you conclude?
Use the figure for Exercises 1–6. Find each
measure if HG and HI are midsegments.
1. HI ___________________
2. DF ___________________
3. GE ___________________
4. mHIF ___________________
5. mHGD ______________
6. mD ___________________
7. InXYZ, XY  9.3, YZ  7.6, and XZ  8.05. Name the largest and smallest angles ofXYZ.
________________________________________________________________________________________
8. InJKL, mJ  62 and mK  57. Name the longest and shortest sides ofJKL.
________________________________________________________________________________________
In each figure, list the segments in order from longest to shortest.
9.
10.
Tell whether a triangle can have sides with the given lengths. If not, show why.
11. 8, 8, 16 _______________ 12. 0.5, 0.7, 0.3 ________
1
13. 10 , 4, 14 ________
2
14. 3x  2, x2, 2x when x  4 _____________________________________________________
15. 3x  2, x2, 2x when x  6 _____________________________________________________
The lengths of two sides of a triangle are given. Find the range of
possible lengths for the third side.
16. 8.2 m, 3.5 m
________________________
17. 298 ft, 177 ft
________________________
Find the range of values for the variable in each diagram.
19.
20.
18. 3
1
mi, 4 mi
2
________________________
Name _______________________________________ Date __________________ Class __________________
Original content Copyright © by Holt McDougal. Additions and changes to the original content are the responsibility of the instructor.
Holt McDougal Geometry