Download 5.4 Equilateral and Isosceles Triangles

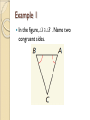
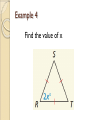
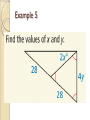
5.4 Equilateral and Isosceles
Triangles
OBJ: Students will be able to use the Base Angles
Theorem and isosceles/equilateral triangles.
Definitions
Leg: congruent sides
 Vertex Angle: angle formed by the legs.
 Base: third side of an isosceles triangle
 Base Angles: two angles adjacent to the
base

Base Angles Theorem

If two sides of a triangle are congruent,
then the angles opposite them are
congruent.
Converse of Base Angles Theorem

If two angles of a triangle are congruent,
then the sides opposite them are
congruent.
Example 1

In the figure, A  B . Name two
congruent sides.
Example 2
Corollaries
Corollary to the Base Angles
Theorem: If a triangle is equilateral, then
it is equiangular.
 Corollary to the Converse Base
Angles Theorem: If a triangle is
equiangular, then it is equilateral.

Example 3

Find the measures of P, Q, and R
Example 4
Find the value of x.
Example 5
Example 6