* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Unit 4 Lesson 5 Congruent Triangles
Penrose tiling wikipedia , lookup
Multilateration wikipedia , lookup
History of geometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Dessin d'enfant wikipedia , lookup
Apollonian network wikipedia , lookup
Trigonometric functions wikipedia , lookup
Technical drawing wikipedia , lookup
Euler angles wikipedia , lookup
Pythagorean theorem wikipedia , lookup
History of trigonometry wikipedia , lookup
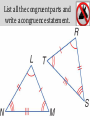
KITE ASSEMBLY Tanya is following directions for making a kite. She has two congruent triangular pieces of fabric that need to be sewn together along their longest side. The directions say to begin sewing the two pieces of fabric together at their smallest angles. At which two angles should she begin sewing? Answer: A and D Honors Geometry Unit 4 Lesson 5 Proving Triangles Congruent Objectives • I can identify corresponding parts of congruent triangles • I can use the definition of congruent triangles • I can discover and apply theorems about triangles Recall • Congruent polygons – All sides are congruent (same length) – All angles are congruent (same measure) • Congruent triangles – 3 congruent sides – 3 congruent angles – Total of 6 congruent parts Corresponding Parts • When two (or more) polygons are congruent, it is necessary to identify their corresponding parts – Use dash marks on sides and arcs on angles! • Corresponding parts – between congruent polygons, corresponding parts have the same measure and are found in the same position – Corresponding parts = matching parts – CPCF (Corresponding parts of congruent figures) Locate Corresponding Parts Identify Corresponding Parts Identify all of the congruent corresponding parts. Mark them on the diagram using the appropriate symbols. Angles: Sides: Congruence Statements • Write a valid congruence statement by listing corresponding parts in the same order – Corresponding parts will appear in the same position – Also, you can read a congruence statement and determine which parts are corresponding Example – Congruence Statement • Same example: • Corresponding parts: • Congruence Statement: Example - Congruence Statement • Statement: • Notice: Since angles A and H were congruent, they appear first (same as B & J, C & K) • Notice: Segments AB and HJ are congruent, and those two letters appear first… • There are multiple correct answers! Write a congruence statement for the triangles. A. ΔLMN ΔRTS B. ΔLMN ΔSTR C. ΔLMN ΔRST D. ΔLMN ΔTRS A. B. C. D. A B C D Name the corresponding congruent angles for the congruent triangles. A. L R, N T, M S B. L R, M S, N T C. L T, M R, N S D. L R, N S, M T A. B. C. D. A B C D List all the congruent parts and write a congruence statement. Algebra In the diagram, ΔITP ΔNGO. Find the values of x and y. O P mO = mP 6y – 14 = 40 6y = 54 y= 9 CPCF Definition of congruence Substitution Add 14 to each side. Divide each side by 6. Algebra In the diagram, ΔITP ΔNGO. Find the values of x and y. NG = IT x – 2y = 7.5 x – 2(9) = 7.5 x – 18 = 7.5 x = 25.5 CPCF Definition of congruence Substitution y=9 Simplify. Add 18 to each side. Algebra In the diagram, ΔFHJ ΔHFG. Find the values of x and y. A. x = 4.5, y = 2.75 B. x = 2.75, y = 4.5 C. x = 1.8, y = 19 D. x = 4.5, y = 5.5 A. B. C. D. A B C D Congruent Triangles • For the rest of the lesson, we will focus on proving that triangles are congruent • Recall that congruent triangles share 6 corresponding, congruent parts • There are 4 shortcuts – ways to show that all six parts are congruent by only using 3 – You only have to do half the work! The Four Congruence Postulates • You must follow the specific order named by the postulate • A – a pair of congruent angles • S – a pair of congruent sides • Included angle – an angle found between two congruent sides • Included side – a side found between two congruent angles SSS Congruence SAS Congruence ASA Congruence AAS Congruence Notice… • There is a combination of letters that we did NOT use – because it will NOT prove that all 6 parts are congruent • One angle and the next two sides… or two sides and the next angle Hints… • To determine WHICH of the 4 postulates is illustrated in a particular example – Read all given information – Use the information to find congruent parts – Find any other congruent parts • Vertical pairs, shared side, etc – Mark congruent parts on the diagram – Determine in which order the parts appear • Is a side between two marked angles? • Is an angle between two marked sides? Determine which postulate can be used to prove that the triangles are congruent. If it is not possible to prove congruence, choose not possible. A. SSS B. ASA C. SAS D. not possible A. B. C. D. A B C D Determine which postulate can be used to prove that the triangles are congruent. If it is not possible to prove congruence, choose not possible. A. SSS B. ASA C. SAS D. not possible A. B. C. D. A B C D Determine which postulate can be used to prove that the triangles are congruent. If it is not possible to prove congruence, choose not possible. A. SSA B. ASA C. SSS D. not possible A. B. C. D. A B C D Use SSS congruence… EXTENDED RESPONSE Triangle DVW has vertices D(–5, –1), V(–1, –2), and W(–7, –4). Triangle LPM has vertices L(1, –5), P(2, –1), and M(4, –7). a. Graph both triangles on the same coordinate plane. b. Use the distance formula to make a conjecture as to whether the triangles are congruent. Explain your reasoning. Find the side lengths of the two triangles Triangle DVW Triangle LPM CONCLUSION: DVW LPM by SSS Congruence Use SSS Congruence Determine whether ΔABC ΔDEF for A(–5, 5), B(0, 3), C(–4, 1), D(6, –3), E(1, –1), and F(5, 1). A. yes B. no C. cannot be determined 1. 2. 3. A B C Video Clip: Proof • http://ed.ted.com/lessons/scott-kennedy-howto-prove-a-mathematical-theory • 4:39 • Open browser first Use SAS to Prove Triangles are Congruent Draw a picture Given:EI HF; G is the midpoint of both EI and HF. Prove: ΔFEG ΔHIG Statements Reasons 1. EI HF; G is the midpoint of EI; G is the midpoint of HF. 1. Given 2. 2. Midpoint Theorem 3. FGE HGI 3. Vertical Angles Theorem 4. ΔFEG ΔHIG 4. SAS Statements 1. Reasons 2. 2. _________ ? Property 3. ΔABG ΔCGB 3. SSS 1. Given A. Reflexive B. Symmetric C. Transitive D. Substitution A. B. C. D. A B C D Recap