Download chapter 4 test_regular

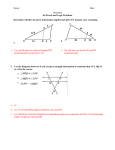
Name ____________________
Geometry
Chapter 4
Test
Date ________
Hint: Draw and label # 4 and #5 before you start scratching your head ♥
6. Write a two-column proof.
7.
9.
Mark your
drawing
Mark your
drawing
WXYZ  JKLM. List each of the following. Please, oh please, use good notation♥
10. four pairs of congruent sides
11. four pairs of congruent angles
ABCD  FGHJ. Find the measures of the given angles or lengths of the given sides.
12. mB = 3y, mG = y + 50
13. CD = 2x + 3; HJ = 3x + 2
For 14, 15 & 16, could you use a shortcut to prove the triangles congruent?
If so, list the corresponding congruent sides.
If there is not enough information, write not enough information and explain your answer.
14.
15.
16
Algebra Find the values of m and n.
17.
18.
19.
m= ______
m= ______
m= ______
n= ______
n= ______
n= ______
What additional information would prove each pair of triangles congruent by the
Hypotenuse-Leg Theorem?
20.
21. What does CPCTC stand for?
22. When is it legal to use CPCTC?
23. Using a compass and straightedge, create an
equilateral triangle with sides AB
A______________________B
Matching
1
_______
proof
A.
A pair of angles created when two lines intersect.
2
_______
theorem
B.
Two angles whose sum is 180 degrees.
3
_______
construction
C.
An adjacent pair of angles whose sum is 180 degrees.
4
_______
area
D.
A pair of angles whose sum is 90 degrees.
5
_______
adjacent angles
E.
A pair of angles that share a vertex, share a ray, and do not overlap.
6
_______
parallel lines
F.
Lines that have the same slope that never intersect.
7
_______
skew lines
G.
In three dimension, lines that never intersect and are not parallel.
8
_______
supplementary angles
H.
A line that intersects two or more other lines.
9
_______
isosceles
I.
A line, ray, or segment that cuts something in half.
10
_______
equiangular
J.
Exactly the same size and shape.
11
_______
circumference
K.
Same shape, different size.
12
_______
vertical angles
L.
Having sides whose lengths are equal.
13
_______
perimeter
M.
Having the same angle measures.
14
_______
transversal
N.
A piece of a line with two endpoints.
15
_______
angle
O.
A point in the middle of a segment.
16
_______
segment
P.
The intersection of the endpoints of two rays.
17
_______
corollary
Q.
Having at least two congruent sides.
18
_______
congruent
R.
A step by step method where something is proved.
19
_______
similar
S.
The product of using a straightedge and compass to create drawings.
20
_______
postulate
T.
The square units contained in a region.
21
_______
complementary
U.
The distance around a region.
22
_______
perpendicular
V.
The distance around a circle.
23
_______
equiangular
W.
A rule that has been proven and has no counterexamples.
24
_______
equilateral
X.
An idea that makes so much sense that we don't need to prove it.
25
_______
bisector
Y.
A notion that naturally follows a theorem.
26
_______
midpoint
Z.
Meeting at a right angle.