Download Image Enhancement in the Spatial Domain

Histogram Processing
• The histogram of a digital image with gray levels in
the range [0, L-1] is a discrete function h(rk) = nk
where rk is the kth gray level and nk is the number of
pixels in the image having gray level rk.
• For practical applications, one has to normalize a
histogram by dividing each of its values by the total
number of pixels in the image, n.
• Thus p(rk) gives an estimate of the probability of
occurrence of gray level rk.
• The sum of all components of a normalized
histogram is equal to 1.
Histogram Processing
• Histogram techniques are used in image compression and
segmentation.
• Let us see gray level images which are dark, light, low-contrast
and high contrast and its corresponding histograms.
• For a dark image, histogram is on the low (dark) side of gray
scale.
• For a bright image, histogram is biased towards high side of the
gray scale.
• An image with low contrast has a histogram that is narrow and
centered toward the middle of the gray scale.
• This implies a dull, washed-out gray look.
• An image whose pixels is occupying entire range of gray levels
and distributed uniformly, has high contrast and show variety of
gray tones.
• Thus it has a high dynamic range.
• It is also possible to develop a transformation function that can
automatically achieve this effect, based on information in the
histogram of the input image.
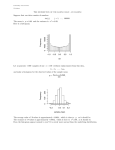
Dark Image
Histogram of dark image
2000
1800
1600
1400
1200
1000
800
600
400
200
0
0
0.1
0.2
0.3
Bright Image
0.4
0.5
0.6
0.7
0.8
0.9
1
Histogram of Bright Image
2500
2000
1500
1000
500
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Low-contrast Image
Histogram of Low-contrast Image
2500
2000
1500
1000
500
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Histogram of High-contrast Image
High-contrast Image
6000
5000
4000
3000
2000
1000
0
0
50
100
150
200
250
Contrast Stretch
• One of the simple techniques to expand the
histogram to fill entire gray-scale range is
contrast stretch or full-scale histogram stretch.
• Commercial digital video cameras for home and
professional use a full-scale histogram stretch to
the acquired image before being stored in
camera memory.
• It is called as automatic gain control (AGC) on
these devices.
Contrast Stretch
• Let f has a compressed histogram with maximum graylevel value B and minimum value A.
•
A = min{f(x,y)}
B = max{f(x,y)}
• We need to find an operation that maps gray levels A
and B in the original image to gray levels 0 and K-1 in
the transformed image. This is expressed as:
•
PA + L =0
• And
PB + L = K-1
• Solving for the unknowns (P,L), the solutions are:
P = (K – 1)/(B – A)
• And
L = -A* (K -1)/(B – A)
• Hence the overall full scale histogram stretch is given as:
•
g(x,y) = ((K -1)/(B – A))* (f(x,y) – A).
Histogram Equalization
• It is one of the important nonlinear point
operations. Contrast stretch tries to fill the
available gray-scale range.
• But here we insist that it should be uniformly
distributed over the range.
• Hence its goal is to produce a flat histogram.
• An image with a perfectly flat histogram contains
largest possible amount of information
Histogram Equalization
• Assume that the intensity levels are continuous
quantities normalized to the range [0,1] and let
pr(r) denote the probability density function
(PDF) of the intensity levels in a given image.
• Let us perform the transformation on the input
levels to obtain output (processed) intensity
levels, s,
•
s = T(r) = integrate (pr(w)dw
• Here w is the dummy variable of integration. We
want the probability density function of the
output levels is to be uniform; that is
•
Ps(s) = 1 for 0 ≤ s ≤ 1
=
0
otherwise
Histogram Equalization
• This transformation increases dynamic range and lead to
higher contrast.
• But this transformation is nothing but the cumulative
distribution function (CDF).
• For discrete quantities, we work with summations and
the equalization transformation becomes
•
sk = T ( rk)
•
= Σ pr(rj) for j = 1 to k
•
= Σ (ni/n) for j = 1 to k and k varies from
1,2, …, L.
• Here sk is the intensity value in the output image
corresponding to value rk in the input image.
Original Image
Histogram Equalized Image
Cumulative probability function
Hostogram of Original Image
1
1600
0.9
1400
0.8
Number of Occurrence
1200
0.7
1000
0.6
800
0.5
600
0.4
400
0.3
200
0.2
0.1
0
Gray Levels
0
50
100
150
200
250
0
0
50
100
150
200
250
300
Histogram of Equalized Image
Cumulative probability function
1
1600
0.9
1400
Number of Occurrence
0.8
1200
0.7
1000
0.6
800
0.5
600
0.4
400
0.3
200
0.2
0.1
0
Gray Levels
0
50
100
150
200
250
0
0
50
100
150
200
250
300
• histogram equalization
• % Read a gray scale image and 1. compute the
cumulative probability
• % function and plot it. 2. scale the cumulative probability
function 0 - 1 to
• % 0 - 256. 3. Map each histogram values H(s)to
probability density value
• % Pf(s). 4. compute the cumulative probability value and
plot
• clear all; close all; clc;
• a = imread('cameraman.tif');
• %a = imnoise(a,'salt & pepper',0.1);
• [m n]=size(a);
• figure,imshow(a);
• figure,imhist(a);
• a = double(a);
• gmin = min(min(a));
• gmax = max(max(a));
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
% Cumulative probability function Pf.
Pf = zeros(1,256);
for i=1:m
for j=1:n
f = a(i,j) +1;
for x = f:256
Pf(x) = Pf(x) +1;
end
end
end
Pf = Pf / (m*n);
figure,plot(Pf);
% histogram equalization
g1 = (gmax - gmin) * Pf + gmin;
figure,plot(g1);
B1 = zeros(m,n);
for i=1:m
for j=1:n
B1(i,j)=g1(a(i,j)+1);
end
end
figure,imshow(uint8(B1));
figure,imhist(uint8(B1));
% Cumulative probability function Pf
Pf = zeros(1,256);
for i=1:m
for j=1:n
f = round(B1(i,j))+1;
for x = f:256
Pf(x) = Pf(x) +1;
end
end
end
Pf = Pf / (m*n);
figure,plot(Pf);
Histogram Matching (Specification)
• Histogram equalization automatically determines
a transformation function that seeks to produce
an output image that has a uniform histogram.
• But there are applications where uniform
histogram is not required.
• In fact, one has to specify the shape of the
histogram that we want the processed image to
have.
• The method used to generate a processed
image that has a specified histogram is called
histogram matching or histogram specification.
Histogram Matching (Specification)
• Once again consider the continuous gray levels
r and z and let pr(r) and pz(z) denote their
corresponding continuous probability density
functions.
• Here r and z denote gray levels of input and
processed output images.
• We can estimate pr(r) from the given input
image, while pz(z) is the specified probability
density function that we wish the output image to
have.
Histogram Matching (Specification)
• Let s be a random variable with the property
•
s = T(r) = integration pr(w) dw where w is the
dummy variable.
• This expression is the continuous version of histogram
equalization.
• Let us define a random variable z with the property
•
G(z) = integration pz(t) dt = s where t is the dummy
variable.
• From these 2 equations, we see G(z) = T(r) and z satisfy
the condition
•
z = G-1(s) = G-1[T(r)].
• The transformation T(r) can be obtained once pr(r) has
been estimated from the input image.
• Similarly the transformation function G(z) can be
obtained once pz(z) is given.
Histogram Matching (Specification)
• In a nutshell, the procedure to be followed is as
follows:
• Obtain the transformation function T(r) from
input image
• Obtain the transformation function G(z) from
specified image
• Obtain the inverse transformation function G-1
• Obtain the output image z by applying the last
equation for all the pixels in the input image.
• This results in an image whose gray levels z,
have the specified probability density function
pz(z).
Dark Image
Bright Image
After Equalization
After Equalization
Low-contrast Image
High-contrast Image
After Equalization
After Equalization
Gaussian Equalization Curve
Histogram of the Original image
0.014
7000
0.012
0.01
Probability density
5000
4000
3000
2000
0.008
0.006
0.004
1000
0.002
0
Intensity levels
0
50
100
0
150
200
250
0
50
100
150
Intensity levels
Histigram equalized Image
7000
6000
Number of Occurrence
Number of Occurrence
6000
5000
4000
3000
2000
1000
0
Intensity levels
0
50
100
150
200
250
200
250
300
Original image
Histogram of the Enhanced Image
• % Histogram Matching
• % Read a gray Scale Image and look at its histogram
• % Generate the bimodel Gaussian function with
appropriate parameters
• % match the given image histogram with the bimodal
gaussian function and
• % verify the resultand image histogram aganist bimodal
gaussian
• clear all; close all; clc;
• f = imread('moon.tif');
• figure,imhist(f);
• f1 = histeq(f,256);
• p = twomodegauss(0.15,0.05,0.15,0.15,0.4,0.8,0.002);
• f2 = histeq(f,p);
• figure,imshow(f);
• figure,plot(p);
• figure,imshow(f2);
• figure,imhist(f2);
Local Enhancement
• The Histogram Equalization and Matching
methods are global in nature.
• The pixels are modified by a transformation
function based on the gray-level content of an
entire image.
• There are cases where we need to enhance
details over small areas in an image.
• Now we need to devise transformation functions
which are based on the neighborhood of every
pixel in the image.
Local Enhancement
• The procedure is to define a square or rectangular
neighborhood and move the centre of this area from
pixel to pixel.
• At each location, the histogram of the points in the
neighborhood is computed and either a histogram
equalization or histogram specification transformation
function is obtained.
• This function is used to map the gray level of the pixel
centered in the neighborhood.
• The centre of the neighborhood region is then moved to
an adjacent pixel location and the procedure is repeated.
• To reduce computation, we can use non-overlapping
regions, but this method produces an undesirable check
board effect.
• Local histogram equalization reveals the presence of
small details.
Original Image
Local Histogram Enhanced Image
Histogram statistics for Image
Enhancement
• We can also use some statistical parameters obtainable from
the histogram also for enhancement.
• Let r denote a discrete random variable representing discrete
gray-levels in the range [0, L-1] and let p(ri) (probability of
occurrence of gray level ri) denote the normalized histogram
component corresponding to the ith value of r.
• The nth moment of r about its mean is defined as
•
μn(r) = Σ (ri – m)n p(ri) where i varies from 0 to L-1.
• Here m is the mean value of r:
•
m = Σ ri p(ri) for i = 0 to L-1
• We notice that μ0 = 1 and μ1 = 0. The second moment is
given by
•
Μ2(r) = Σ (ri – m)2p(ri) for i=0 to L-1.
• This expression is the variance of r, denoted as σ2(r). The
standard deviation is the square root of the variance.
Histogram statistics for Image
Enhancement
• As far as enhancement is concerned, we are
interested in the mean, which is a measure of
average gray level in an image and the variance
which is a measure of average contrast.
• Global mean and variance are measured over
an entire image and are useful for gross
adjustments of overall intensity and contrast.
• In the case of local enhancement, the local
mean and variance are used as the basis for
making changes that depend on image
characteristics in a predefined region about each
pixel in the image.
Histogram statistics for Image
Enhancement
• Let (x,y) be the coordinates of a pixel in an image and let
Sxy denote a neighborhood (subimage) of specified size,
centered at (x,y).
• The mean mSxy of the pixels in Sxy is calculated as
•
mSxy = Σ rs,t p(rs,t)
• where rs,t is the gray level at coordinates (s,t) in the
neighborhood, and p(rs,t) is the neighborhood normalized
histogram component corresponding to that value of gray
level.
• Similarly the gray-level variance of the pixels in region Sxy
is given by
•
σ2Sxy = Σ [rs,t - mSxy]2 p(rs,t)
• The local mean is a measure of average gray level in
neighborhood
• Sxy and the variance is a measure of contrast in that
neighborhood.
Histogram statistics for Image
Enhancement
• If one part of the image is quite clear and other
part of the image is darker and contain hidden
features of interest, then we can apply local
approaches.
• A measure of whether an area is relatively light
or dark at a point (x,y) is to compare the local
average gray level mSxy to the average image
gray level, called the global mean, MG.
• We can process a pixel at the (x,y) if mSxy ≤ k0MG
where k0 is a positive constant with value less
than 1.0
Histogram statistics for Image
Enhancement
• If we are interested in enhancing areas that have low contrast, we
need a measure to determine whether the contrast of an area
makes it a candidate for enhancement.
• Thus we enhance a pixel at (x,y) if σSxy ≤ k2DG where DG is the
global standard deviation and k2 is a positive constant.
• The value is greater than 1.0 for enhancing light areas and less than
1.0 for dark areas.
• We need to set the lowest values of contrast to accept, otherwise
the procedure would attempt to enhance even constant areas,
whose standard deviation is zero.
• Thus we set a lower limit on the local standard deviation by setting
k1DG ≤ σSxy, with k1 < k2.
• A pixel at (x,y) that meets all the conditions for local enhancement is
processed by multiplying it by a specified constant E, to increase (or
decrease) the value of its gray level relative to the rest of the image.
• Values of pixels not meeting the enhancement conditions are left
unchanged.
Histogram statistics for Image
Enhancement
• In a nutshell, let f(x,y) is the value of an
image pixel at (x,y) and g(x,y) is its
corresponding enhanced pixel at (x,y).
Then
• g(x,y) = E.f(x,y) if mSxy ≤ k0MG AND k1DG
≤ σSxy ≤ k2DG
•
= f(x,y)
otherwise
• Here E, k0,k1 and k2 are specified
parameters and MG and DG are the global
mean and global standard deviation.
Original Image
Image formed from local standard deviation
Image formed from local means
Image formed from all multiplication constants
Enhancement using
Arithmetic/Logic Operations
• Arithmetic operations involving images are done on a
pixel-by-pixel basis between 2 or more images (except
NOT operation which is done on a single image).
• Any logical operations can be implemented using only
AND, OR and NOT logic operators.
• When dealing with gray-scale images, pixel values are
processed as strings of binary numbers.
• The NOT logic operator does the same function as the
negative transformation does.
• The AND and OR operations are used for masking; that
is, for selecting subimages in an image.
• Masking is also called as region of interest (ROI)
processing.
Enhancement using
Arithmetic/Logic Operations
• Of the four arithmetic operations,
subtraction, and addition are useful for
image enhancement.
• Division of 2 images is considered as
multiplication of one image by the
reciprocal of the other.
• Multiplying an image by a constant
increases its average gray level
Image Addition
Image Subtraction
Image Subtraction
• The difference between 2 images f(x,y) and h(x,y) is
given as:
•
g(x,y) = f(x,y) – h(x,y)
• The difference image is very useful for evaluating the
effect of setting to zero the lower-order planes.
• Image subtraction for segmentation is used when the
criterion is “changes”.
• In tracking moving vehicles in a sequence of images,
subtraction is used to remove all stationary components
in an image.
• What is left is the moving elements in the image plus
noise.
(a) Original fractal Image. (b) Result of four lower-order bit plains to zero.
(c) Difference image.
Image Averaging
• Consider a noisy image g(x,y) formed by
addition of noise η(x,y) to an original image.
•
g(x,y) = f(x,y) + η(x,y)
• Here we assume that at every pair of
coordinates (x,y) the noise is uncorrelated and
has zero average value.
• We try to reduce the noise content by adding a
set of noisy images, gi(x,y).
• It can be shown that as the number of noisy
images used in the averaging process
increases, the noisy image resembles the
original image f(x,y).
Image Averaging
• Let ğ(x,y) is obtained by averaging K different noisy
images.
•
ğ(x,y) = (1/K) Σ gi(x,y) where i varies from 1 to K.
• Then
•
E{ ğ(x,y)} = f(x,y)
and
•
σ2 ğ(x,y) = (1/K) σ2 η(x,y)
• Here E{ ğ(x,y)} is the expected value of ğ and σ2 ğ(x,y)
and σ2 η(x,y) are the variances of ğ and η, all at
coordinates (x,y).
• The standard deviation at any point in the average image
is
•
σ ğ(x,y) = (1/sqrt(K)) σ η(x,y)
• Now we realize that as K increases, the variability
(noise) of the pixel values at each location (x,y)
decreases.
Original Image
Averaged Noisy Image
Noisy Image
Difference between Original and Noisy Image
Difference between Original and Averaged Noisy Image
1200
800
1000
600
Number of Occurrence
Number of Occurrence
700
500
400
300
800
600
400
200
200
100
0
0
Intensity Levels
0
50
100
150
Intensity Levels
200
250
0
50
100
150
200
250
% Read a gray scale image and analyze the effect of averave filter(linear)
% for various mask sizes. prove that higher the maks size is leading to
% more blurring
clear all; close all; clc;
f = imread('moon.tif');
f = im2double(f);
%f1 = imnoise(f,'gaussian',0,0.4);
[m n]=size(f);
f2 = zeros(m,n);
% e=input('Enter size of the mask: ');
e = [3,5,9,17];
M_size=(e(1)-1)/2;
A_imge1=Iaver(f,M_size);
M_size=(e(2)-1)/2;
A_imge2=Iaver(f,M_size);
M_size=(e(3)-1)/2;
A_imge3=Iaver(f,M_size);
M_size=(e(4)-1)/2;
A_imge4=Iaver(f,M_size);
figure(1);
subplot(3,2,1),imshow(f);
subplot(3,2,2),imshow(f);
subplot(3,2,3),imshow(A_imge1);
subplot(3,2,4),imshow(A_imge2);
subplot(3,2,5),imshow(A_imge3);
subplot(3,2,6),imshow(A_imge4);