Download WORK AND ENERGY

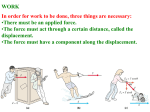
Chapter 6
LECTURE NOTES
WORK AND ENERGY
The concepts of work and energy in mechanics allow us to analyze motion using conservation
principles instead of Newton’s second law. Work and energy are scalar quantities; it is often
easier to solve problems with these instead of vectors.
Work in physics is defined as the scalar product of force and displacement; that is W = F • d.
Work is measured in joules (J), with 1J = 1N۰m.
Example: Find the work done on a box that undergoes a displacement d when pulled by a rope
under tension T inclined an angle  above the horizontal.
N
T

Tx
fk
Ty
d
mg
If there is no friction (   0 ) the work done by the force T is: W = T۰d = T d cos  .
Note: this can be written (T cos  ) d = Tx d; work is the product of a displacement and
the component of the force in the direction of displacement.
The work done by forces N, W (= mg down), and the vector component Ty = 0 as they are ⊥
d and cos 90° = 0.
to
The work done by friction is f۰d = fk d cos 180 = -fkd since cos 180° = -1.
Note: The work done by friction is negative – it ‘steals’ mechanical energy from the
system, converting it mostly into heat.
To continue, we need to use concepts from the last chapter.
fk =  kN =  k (mg – T sin  ) --Do you see why?-- and work done by friction =
-  kd (mg – T sin  ).
The net work (or sum of work due to all forces acting on a body) is
Td cos  -  kd (mg – T sin  ).
Example: An athlete lifting weights must exert an upward normal force greater than or equal to
the force of gravity. If the weights are lifted through a height h then work done by athlete = mgh
and work done by gravity = -mgh (it acts 180° away from displacement) so net work done on
box = 0.
Chapter 6
LECTURE NOTES
Note: If the athlete moves the weight, held overhead, through a horizontal distance x, the
work is mg x cos 90° = 0 if we consider only the upward force exerted.
We can calculate work done by varying forces using calculus or by finding the area under the
curve of a force vs displacement graph. Areas above the displacement axis are positive; below,
negative.
When we stretch (or compress) a spring, it exerts an opposing force proportional to the
displacement. This is Hooke’s law F = -kx where k is the spring constant (units N/m). The work
1
done by the spring is the area of the triangle shown =  kx2 ((the work done by the person x
2
1 2
stretching the spring is + kx .
2
We have stored elastic potential energy in the stretched
F
(compressed) spring  elastic = -Wspring = +1/2 kx2.
x
Potential energy can also be defined for our weight lifting
example where  = - Wgravity = +mgh. The units of
potential energy are the units of work (joules).
The zero point of potential energy is arbitrary; it is 
that matters. Thus we can let PE = 0 when the weights
-kx
are on the ground or high overhead and all will work out in the end without any problem.
Usually we pick the lowest level to be y = 0 and then PE = 0 since PEgravity = mgy.
Kinetic energy is the energy associated with motion as opposed to position. We define
KE = ½ mv2 where the units are again joules (J). It can be shown that the net work done by all
forces acting on a body change its kinetic energy according to the work – energy principle: (PE
constant).
Wnet =  = KE final – KE initial. If + net work is done on a body, its KE increases; if – net work
is done on a body, its KE decreases.
Example: A 10.0kg penguin is sliding on level ice (  k = 0.100). If his initial velocity is 2.00
m/s, how far will he slide? Use Wfriction =  and write fk ۰ x = KEinitial; using fk =  kN,
-  k mg x = 0 – 1/2mvi2; x is the final position or displacement if we start at 0.
1
2
2
mv i
x=
≈ 2.00m.
 k mg
A more general formulation of the work-energy principle where PE is allowed to vary states W
done by non-conservative forces =  +  . Conservative forces are those for which PE
can be defined; the work done by these forces depends only on initial and final positions, not the
path chosen. Non-conservative forces (friction is the main example) are those which steal
mechanical energy from a system converting it into some other form of energy.
Chapter 6
LECTURE NOTES
Conservation of Mechanical Energy
If there is no friction (  k = 0) we have 0 =  +  (the total mechanical energy is
conserved) or KEi +PEi = KEf + PEf.
If there is friction we write KEi + PEi – fkd = KEf + PEf if the frictional force fk acts over a
displacement d.
Example: Penguins are sliding on wet ice (assume frictionless). They begin with vi = 4.00 m/s,
but slide up a hill inclined an angle  above the horizontal. How far up the hill will they slide?
Use conservation of mechanical energy KEi + PEi = KEf + PEf. Let y = 0 at start, find final y.
1
1
2
2
mv i  mgy : mv f  mgy f
2
2
1
2
mv i + 0 = 0 + mgyf
2
2
v
yf = i ≈ 0.800m
2g
y
The slant distance along the incline =
.
sin 
Example: Jumpin' Jack Flash was a London criminal with powerful springs in his boots to allow
him to jump over walls and elude pursuers. To raise a 50.0kg man 1.00m above his normal
jump, what energy must be stored in the spring. This would be the  or mgh of the man ≈
550J. To store this in springs with reasonable compression required very stiff (high k) springs.
Power
Power is the rate at which work is done P = W/t). The units are watts (W); 1 W = 1 J/s. The
ft  lb
British unit is the horsepower; 1 hp = 550
= 746 W.
s
Note: P =
W Fd

= Fv
t
t
Example: What power is exerted when a 60kg student climbs a 4.50m (vertical) stair in 4.0s?
P=
mgh
= 588W.
t