Download work

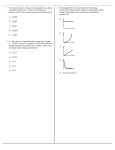
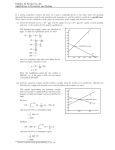
Energy and Work
Energy - the ability of a
body or system of bodies to
perform work.
A body is given energy when
a force does work on it.
But What is Work?
A force does work on a body
(and changes its energy) when it
causes a displacement.
If a force causes no
displacement, it does no work.
Riddle Me This
If a man holds a 50 kg box at arms
length for 2 hours as he stands still, how
much work does he do on the box?
ZERO
NONE
Counterintuitive Results
 There is no work done by a force
if it causes no displacement.
 Forces perpendicular to
displacement, such as the normal
force, can do no work.
 Likewise, centripetal forces
never do work.
Calculating Work
Work is the dot product of
force and displacement.
Work is a scalar resulting
from the interaction of two
vectors.
Vector Multiplication
There are three ways to multiply
vectors:
•Scalar Multiplication
•Dot Product
•Cross Product
Scalar Multiplication
•Magnitude of vector changes.
•Direction of vector does not change.


F  ma
If m = 5 kg
a = 10 m·s-1
F = 50 N
Dot Product
Note that the dot
 
W  A  B product of two vectors
gives a scalar .
 
A  B  AB cos



 is the angle between A and B.

A
θ

B
Dot Product
Geometrically, the dot product is the
projection of one vector on a second
vector multiplied by the magnitude of
the second vector.

A
θ
A cos

B
Calculating Work
 
W  F  s  Fs cos

F
θ
F cos 

s
W   F ( x)dx
Which does more work?
Two forces are acting on the box
shown causing it to move across the
floor. Which force does more work?
F2
θ
F1
Vectors and Work
F
Vectors and Work
F
s
W=F•s
W = F s cos 0o
W=Fs
Maximum positive work
Vectors and Work
F
Vectors and Work
F

s
W=F•s
W = F s cos 
Only the component of force aligned
with displacement does work. Work is
less.
Vectors and Work
F
Vectors and Work
F

s
W=F•s
W = F s cos 180o
W=-Fs
Maximum negative work.
Gravity often does
negative work.
When the load goes up, gravity does negative
work and the crane does positive work.
When the load goes down, gravity does
positive work and the crane does negative
work.
F
mg
Positive, zero, or negative work?
A box is being moved with a velocity v
by a force P (parallel to v) along a
level floor. The normal force is FN, the
frictional force is fk, and the weight of
the box is mg.
Decide which forces do positive, zero,
or negative work.
Positive, zero, or negative work?
v
FN
fk
P
mg
s
Units of Work
 
W  F  s  Fs cos
J = N·m
J=
2
-2
kg·m ·s
Work and variable force
The area under the
curve of a graph of
force vs
displacement gives
the work done by
the force.
F(x)
xb
W = x F(x) dx
a
xa
xb
x
Net Work
Net work (Wnet) is the sum of the work
done on an object by all forces acting
upon the object.
The Work-Energy Theorem
• Consider a force applied to an object
(ΣF ≠ 0).
• Newton’s second law tells us that this
net force will produce an acceleration.
• Since the object is accelerating, its
displacement will change, hence the
net force does work.
The Work-Energy Theorem
 FWs  mas
 F  ma
(v  v ) 2
W
W
 mmv  mvi
2
2
2
f
f
1
2
2
1i
2
 F s  W
v  v  2as
(v  v )
 as
2
2
f
2
f
2
i
2
i
Kinetic Energy
A form of mechanical energy
Energy due to motion
K = ½ m v2
– K: Kinetic Energy in Joules.
– m: mass in kg
– v: speed in m/s
The Work-Energy Theorem
 F  ma
W  mas
W  mv  mv
1
2
2
f
1
2
2
i


KE
Wnet
The Work-Energy Theorem
Wnet = KE
– When net work due to all forces acting upon
an object is positive, the kinetic energy of the
object will increase.
– When net work due to all forces acting upon
an object is negative, the kinetic energy of the
object will decrease.
– When there is no net work acting upon an
object, the kinetic energy of the object will be
unchanged.
Power
Power is the rate of which work is
done.
No matter how fast we get up the
stairs, our work is the same.
When we run upstairs, power demands
on our body are high.
When we walk upstairs, power
demands on our body are lower.
Power
The rate at which work is
done.
Pave = W / t
P = dW/dt
P = F • v
Units of Power
Watt = J/s
ft lb / s
horsepower
• 550 ft lb / s
• 746 Watts
Power Problem
Develop an expression for the
power output of an airplane cruising
at constant speed v in level flight.
Assume that the aerodynamic drag
force is given by FD = bv2. By what
factor must the power be increased
to increase airspeed by 25%?
How We Buy Energy…
The kilowatt-hour is a commonly used unit
by the electrical power company.
Power companies charge you by the
kilowatt-hour (kWh), but this not power, it
is really energy consumed.
1 kW = 1000 W
1 h = 3600 s
1 kWh = 1000J/s • 3600s = 3.6 x 106J
More about force types
 Conservative forces:
– Work in moving an object is path independent.
– Work in moving an object along a closed path is zero.
– Work may be related to a change in potential energy or
used in the work-energy theorem.
– Ex: gravity, electrostatic, magnetostatic, springs
 Non-conservative forces:
– Work is path dependent.
– Work along a closed path is NOT zero.
– Work may be related to a change in total energy
(including thermal energy).
– Ex: friction, drag, magnetodynamic
Mechanical Energy:
Potential energy
Energy an object possesses by virtue
of its position or configuration.
Represented by the letter U.
Examples:
– Gravitational potential energy.
– Electrical potential energy.
– Spring potential energy.
Gravitational Potential
Energy (Ug)
For objects near the earth’s surface,
the gravitational pull of the earth is
constant, so
Wg = mgx
– The force necessary to lift an object at
constant velocity is equal to the weight,
so we can say
Ug = -Wg = mgh
Where is Gravitational
Potential Energy Zero?
Ug has been defined to be zero when
objects are infinitely far away, and
becoming negative as objects get closer.
This literal definition is impractical in
most problems.
It is customary to assign a point at which
Ug is zero. Usually this is the lowest point
an object can reach in a given situation
Then, anything above this point is a
positive Ug.
Ideal Spring
Obeys Hooke’s Law.
Fs(x) = -kx
– Fs is restoring force exerted BY the
spring.
Ws =  Fs(x)dx = -k  xdx
– Ws is the work done BY the spring.
Us = ½ k x2
Spring Problem
Three identical springs
(X, Y, and Z) are hung
as shown. When a 5.0kg mass is hung on X,
the mass descends 4.0
cm from its initial
point. When a 7.0-kg
mass is hung on Z,
how far does the mass
descend?
X
Y
Z
System
Boundary
Isolated System
Boundary allows no exchange
with environment.
E = U + K + Eint
= Constant
No mass can enter or leave!
No energy can enter or leave!
Energy is constant, or conserved!
Law of Conservation of
Energy
Energy can neither be created nor
destroyed, but can only be
transformed from one type of
energy to another.
Applies to isolated systems.
Law of Conservation of
Mechanical Energy
E=U+K=C
E = U + K = 0
for gravity
Ug = mghf - mghi
K = ½ mvf2 - ½ mvi2
Law of Conservation of
Mechanical Energy
E=U+K=C
E = U + K = 0
for springs
Ug = ½
K = ½ mvf2 - ½ mvi2
2
kx
Law of Conservation of
Energy
E = U + K + Eint= C
E = U + K +  Eint = 0
Eint is thermal energy.
Mechanical energy may be
converted to and from heat.
James Prescott Joule
Father of Conservation of Energy.
Studied electrical motors.
Derived the mechanical equivalent of heat.
Measured heat of water as it fell.
Measured cooling of expanding gases.
Pendulum Energy
½mvmax2 = mgh
h
For minimum and
maximum points of
swing
½mv12 + mgh1 = ½mv22 + mgh2
For any points two points in the
pendulum’s swing
Spring Energy
0
m
½ kx2 = ½ mvmax2
For maximum and
minimum
displacements from
equilibrium
-x
m
m
x
½ kx12 + ½ mv12 = ½
kx22 + ½ mv22
For any two points in a
spring’s oscillation
Announcements
Clicker Quiz.
Homework Check.
5/7/2017
Spring and Pendulum Energy
Profile
E
Total Energy
U
K
x
Equilibrium
The net force on a system is zero
when the system is at
equilibrium.
There are three types of
equilibrium which describe what
happens to the forces on a system
when it is displaced slightly from
the equilibrium position.
Force and Potential
Energy
In order to discuss the relationships
between displacements and forces,
we need to know a couple of
equations.
W =  F(x)dx = -  dU = -U
 dU = -  F(x)dx
F(x) = -dU(x)/dx
Stable Equilibrium
compressed
U
extended
F = -dU/dx
dU/dx
When x is negative, dU/dx is
negative, so F is positive and pushes
system back to equilibrium.
x
Stable Equilibrium
Examples:
– A spring at equilibrium position.
When the system is displaced
from equilibrium, forces return it
to the equilibrium position.
Often referred to as a potential
energy well or valley.
Stable Equilibrium
compressed
U
extended
F = -dU/dx
dU/dx
When x is positive, dU/dx is
positive, so F is negative and pushes
system back to equilibrium.
x
Stable Equilibrium
compressed
U
extended
F = -dU/dx
When x is zero, dU/dx is zero, so F
is zero and there are no forces on
the system pushing it anywhere.
dU/dx x
Unstable Equilibrium
Examples:
– A cone on its tip.
When the system is displaced
from equilibrium, forces push it
farther from equilibrium position.
A potential energy peak or
mountain.
Unstable Equilibrium
U
F = -dU/dx
dU/dx
When x is negative, dU/dx is
positive, so F is negative and pushes
system further from equilibrium.
x
Unstable Equilibrium
U
dU/dx
F = -dU/dx
When x is positive, dU/dx is
negative, so F is positive and pushes
system further from equilibrium.
x
Unstable Equilibrium
U
F = -dU/dx
When x is zero, dU/dx is zero, so F
is zero and no forces are trying to
push the system anywhere.
dU/dx
x
Neutral Equilibrium
Examples:
– A book on a desk.
When the system is displaced
from equilibrium, it just stays
there.
A potential energy plane.
Neutral Equilibrium
U
F = -dU/dx
dU/dx
When x changes, dU/dx is zero, so F is
zero and no force develops to push the
system toward or away from equilibrium.
x
Potential Energy and
Force
•F(r) = -dU(r)/dr
•Fx = -U/  x
•Fy = -U/  y
•Fz = -U/  z
Equilibrium equations
Stable
–U/x = 0, 2U/x2 > 0
Unstable
–U/x = 0, 2U/x2 < 0
Neutral
2
2
–U/x = 0,  U/x = 0
Atomic bonds and Equilibrium
U
Atoms too close
Atoms too far apart
x
Lowest energy inter-atomic separation