Download 4.6 Basic Input Circuits

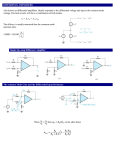
Chapter 4
Basic Electrical Measurements
and Sensing Devices
4.2 Forces of Electromagnetic Origin
F  q( E  v  B )
F  qv  B
dq
d F  dqv  B 
ds B
dt
 i( d s  B )
F

L


L
0
0
i( d s  B )
iBds
F  BiL
if d s  B
4.2 Forces of Electromagnetic Origin
Kx  BiL
BL
x
i
K
 K 
i
 x
 BL 
This is the basic principle of “Current Meters.”
4.2 Forces of Electromagnetic Origin
Analog vs. Digital Representation
Analog: Continuous values
Digital: Discrete values
What is precision?
How fast is it?
4.4 Basic Analog Meters
4.4 Basic Analog Meters
D’Arsonval Galvanometer – DC Current Measurement
4.4 Basic Analog Meters
D’Arsonval Galvanometer – DC Current Measurement
Galvanometer – AC Current Measurement
Iron-vane instrument
Electrodynamometer
4.4 Basic Analog Meters
High Frequency AC Current Measurement –
Thermocouple Meter
4.4 Basic Analog Meters
Voltmeter
4.5 Basic Digital Meters
*The analog meters usually respond
to, and measure, currents.
*The digital meters usually respond
to, and measure, voltages.
A Ramp-type Digital Voltmeter
4.6 Basic Input Circuits
To measure the resistance is important,
many sensors based on resistance change, such as MRAM, RRAM
Consider a Current-sensitive input Circuit
R is the variable to be measured
i
Ei
R  Ri
Rm is the max imun resis tan ce
of the transducer
E i /( R  Ri )
i

i max
E i / Ri

It would be desirable to have the current output
vary linearly with the resistance from transducer.
Unfortunately, this is not the case.
1
( R / Ri )  1
1

( R / Rm )( Rm / Ri )  1
4.6 Basic Input Circuits
Consider a Voltage-sensitive input Circuit
Ei
i
R  Ri


i
E
iR

E i i ( R  Ri )

( R / Rm )( Rm / Ri )
( R / Rm )( Rm / Ri )  1
Non-linear output of R(E) is still obtained.
We define the “sensitivity” of the circuit as:
E i Ri
dE
S

dR
( Ri  R ) 2
dE
 0 i .e ., Ri  R
Maximum sensitivity condition:
dRi
Note: R is a variable
4.6 Basic Input Circuits
In the above two circuits, current measurement has been used as
an indicator of the value of the variable resistance of the
transducer.
Sometimes, it is more convenient to use a Voltage-divider circuit.
Loading effect:
To measure the source voltage
Ideal case Rout=0 and Rin=infinite
However, Rin always limited.
Loading effect
To measure the Rx:
Ideal case: Ri=0
E is known
By measuring A
A = E/Rx
Rx can be measured
However,
Ri is not zero
What should you do?
By a bridge method.
4.6 Basic Input Circuits
Voltage-divider circuit
E
R

E 0 Rm


i
if Ri  R
Usually, Ri will draw some current , therefore
E0
i
( Rm  R )  Ri R /( R  Ri )
the indicated voltage
E  E 0  i ( Rm  R )
R / Rm
E

E 0 ( R / Rm )( 1  R / Rm )( Rm / Ri )  1
Voltage does not vary linearly with Resistance R due to meter
loading error.
4.6 Basic Input Circuits
Improvement in measurement and accuracy is provided by
Bridge circuits – measure resistance, inductance, inductance
Balanced (Null) Wheatstone Bridge
When balance occurs
i 2 R 2  i 1 R1
E
i2  i3 
R2  R3
i1  i x 
E
R1  R x
R2
R
 1
R3 R x
R3
R x  R1
R2
Z3
 Z x  Z1
Z1
Ratio arms : R2 , R3
4.6 Basic Input Circuits
Example 4.3
R x  R1
R3
R2
Other Balanced (or Null) Bridges – for AC Impedances
4.6 Basic Input Circuits
Un-balanced (Deflection) Wheatstone Bridge
The use of the deflection bridge
is important for the measurement
of dynamic signals where
Insufficient time is available for
achieving balance conditions.
ignore Rb
ig 
E b [ R1 /( R1  R4 )  R2 /( R2  R3 )]
R g  [ R1 R4 /( R1  R4 )  R2 R3 /( R2  R3 )]
thus
R4 
E b R1 R 3  i g [ R g R 1 ( R 2  R 3 )  R 2 R 3 R1 ]
i g ( 1  R1  R g )( R2  R3 )  E b R2
4.7 Amplifiers
In many cases, the signals from the transducer and/or input
circuits are comparatively weak and must be amplified
before they can be used to drive an output device.
In other cases, there may be serious “impedance mismatch” inbetween transducer/input circuits and output circuits,
amplifier can provide impedance matching.
4.7 Amplifiers
* Negative Feedback
Without Feedback:
Eo
A
Ei
With Feedback:
Af 
Eo
Eo
A


Ei
E o / A  kE o 1  kA
The amplifier gain is usually very large, i.e., kA  1
A
1
Af 
 : a constant
kA k
The negative feedback greatly extends the “linear input range” of
an amplifier, since the feedback lowers the voltage presented at
the input of the amplifier.
4.7 Amplifiers
* Negative Feedback
4.7 Amplifiers
* Input Impedance
Without Feedback:
Ei
Eo
E
Zi 


Ii
Ii
AI i
With Feedback:
E i  E o k  1 / A
E
E k  1 / A
Zi, f  i  o
Ii
E o / AZ i
 Z i ( 1  kA )
Negative voltage feedback increase the input impedance by a
factor of 1+kA
4.7 Amplifiers
* output Impedance
E o  AE  I o Z o
For E i  0 , E  -kE o
E o   AkE o  I o Z o
Eo 
Zo, f
Io Zo
1  kA
E
Zo
 0 
Io
1  kA
Negative voltage feedback lower the output impedance by a
factor of 1+kA
4.7 Amplifiers
Negative feedback can also reduce the amplifier noise which is
present in the output signal.
Without feedback:
E o  AE i  N
With feedback:
E  E i  kE o
E o  AE  N
 A E i  kE o   N
AE i  N
1  kA
For kA  1
Eo 
Eo 
Ei
N

k
kA
Example 4.5
4.8 Differential Amplifiers
Common-Mode Rejection Ratio (CMRR)
CMRR  20 log
Ad
Acm
Values greater then 120dB are common.
4.9 Operational Amplifiers
An op-amp is a dc differential amplifier incorporating many solidstate elements in a compact package.
Ri - infinite; Ro -- zero
Active circuit
Passive circuit
4.9 Operational Amplifiers
Adder
4.9 Operational Amplifiers
Analogy computer to solve ordinary differential equation
4.10 Transformers
Transformers can also be used for matching impedance.
Input impedance Z 1
Output Impedance Z 2
Z2  n2 Z1
Example:
Loudspea ker Input impedance
Z 1  3Ω
Op Amp Output Impedance
Z 2  50 Ω
Use a transformer with n=4
between Amp and LS will provide
almost Max. power output!
4.12 Signal Conditioning
Various filters and their combinations can be used to reduce the
effect of noises with various frequency ranges.
4.12 Signal Conditioning
First-Order Low-Pass Filters
First-Order High-Pass Filters
4.12 Signal Conditioning
Second-Order Low-Pass Filter
4.12 Signal Conditioning
Second-Order High-Pass Filter
Second-Order Band-Pass Filter
4.12 Signal Conditioning
Active Filters
Low-Pass Filter
High-Pass Filter
Band-Pass Filter
DAC circuit
Daul-slope ADC
Successive Approximation type ADC
Staring from MSB ( Max. Significant Bit)
Lockin
Amplifier
Bandpass filter
(signal fixed frequency)
Plus
Timing (phase)
Noise:
Different frequency
Random phases
Photoluminescence (PL) equipment with locking amplifier
Auger electron spectroscopy using locking amplifier
Anaolgy data -> signal conditioner-> plotter, display, anology output
Analogy data ->ADC ->FIFO buffer -> memory->mass storage
Digital data -> DAC -> plotter, display, oscilloscope
data transmission:
By analogy
Frequency modulation
Amplitude modulation
By digital
Coding-ASCII code, binary code, gray code, parity check
Communication Protocols:
RS232, USB, GPIB(General purpose interface bus(IEEE-488))
4.19 Sensors and Transducers
* Sensor (Latin: sentire: to perceive)
is a device that responds to a physical (or chemical) stimulus (such
as heat, light, sound, pressure, magnetism, or a particular
motion) and transmits a resulting impulse (as for measurement
or operating a control).
* Transducer (Latin: transducere: to lead across)
* Sensor and Transducer are synonymous terms.
* We generally reserve the word sensor for a device that detects or
measures an input signal, and the word transducer for a device
which performs subsequent transduction operation in an
measurement or control system.
4.19 Sensors and Transducers – Sensor Characteristics
4.19 Sensors and Transducers – Sensor Characteristics
O/P Signal, O/P Range, O/P Noise
O/P Impedance, O/P Power,...
Input Range (overload, overrange)
Loading Effects
Mechanical Coupling,. ..
Temperature, Pressure, Vibration,
Acceleration, Mounting Effect,...
4.19 Sensors and Transducers – Sensor Characteristics
(a) Static Characteristics :
Accuracy (Calibration), Precision (repeatability),
Reproducibility, Linearity, Bias, Offset,
Sensirivity, Resolution, Hysteresis, drift
Dead Band, Threshold, Saturation,...
(b) Dynamic Characteristics :
Time Response, Transient Response,
Steady - State Response,
Frequency Response, ...
4.20 The Variable – Resistance Transducer
* Variable Resistance Transducer (also called Resistance
Potential-meter or Rheostat): is a device to convert either
linear or angular displacement into an electric signal.
(a) Potentialmeters
The output vo is proportional
to the rectilinea r displacement x
or the angular displaceme nt 
(b) The Differential Potentialmeter
The output vo is proportional to the
difference of the inputs x1 and x2
4.20 The Variable – Resistance Transducer
(c) Liquid - level Indicator
The resistance between the rods decrease
with the height H of the electrolyt e in the
container.
4.20 The Variable – Resistance Transducer
(d) Strain Measurement
strain :   L / L
resistance : R  L / A
As strain applied, the length
and area change, resulting in
changes in resistance :
R / R0
guage factor G 

where R0 is the resisrance before
the strain. A typical guage has
R0  350 and G  2.0
 for a strain of 1%, R  7 
4.23 Piezoelectric Transducers – An Seismic Instrument
4.21a The Linear Variable Differential Transformer (LVDT)
4.22 Capacitive Transducers
x
A
Capacitance C  0.225
d
where C is in pF, A in in 2 , and d in in
(the constant would be 0.0885 if cm 2 and cm are used for A ans d)
and  is the relative dielectric constant (   1 for air, 3 for plastics)
It can be shown that :
C
C
-
d / d
C A
x
,

(
)
1  ( d / d) C
A
x
4.22 Capacitive Transducers – Example 4.11
C  0.225ε
A
d
4.22 Capacitive Transducers – Example 4.12
4.23 Piezoelectric Transducers
* Piezoelectric Material produce an electric charge when it is
subjected to a force or pressure (and vice versa).
pressure applied

crystal deforms

displaceme nt of charge
within crystal

produce external charges
of opposite sign on
crystal external surface
Q  dF
Q is charge in Coulombs
F is force in Newton, d is the piezoelect ric constant
the output voltage
Q dFt d

 pt  E  gpt
C ' A '
(note : C  '  A/t )
g (Vm/N)  d/' , is the voltage sensitivity
E
4.23 Piezoelectric Transducers – Example 4.13
E  gpt
4.23 Piezoelectric Transducers – An Accelerometer
4.24 Photoelectric Effects
Photoelectric Transducer converts a light beam into a usable
electric signal.
Photo-Multiplier (PM) Tube
4.25 Photoconductive Transducers
* Photoconductive Transducers (Cells) are fabricated from
semiconductor materials (e.g., CdS, PbSe, PbS, InSb,…)
which exhibit a strong photoconductive response.
* Can be used to measure EM radiation at all wavelengths.
photon strike
 generation of e - h pairs
 # of charge carrier 
resistivit y 
4.26 Photovoltaic Cells (Photodiodes)
photon strike
 generation of e - h pairs
in depletion region
 current flow which
produced voltage
4.30 Hall – Effect Transducers

  
F  q(   v  B)
in y - direction Fy  q(  y - v x B z ) :
 y is establishe d via v x B z  Hall Effect
to maintain steady - state flow in
x - directin :
 y  v x Bz
 E H   y  w  v x wBz

Ix
Ix
Jx 

A tw
J x  qp0  v x where
p0 is the hole concentration
Jx
1 Ix
 w  Bz 
 w  Bz
qp0
qp0 t  w
I x Bz
 E H  RH 
t
where I x : A, B z : G, t : cm, and
V  cm
RH :
is called the Hall coefficient
AG
4.23 Piezoelectric Transducers – Example 4.16
Chapter 4 Sensing Devices
Any questions?
Exercises:
4.6
4.8
4.19
4.23
4.25
4.55
Further study: control engineering;
experimental lab: 儀器與量測實驗; 近代物理實驗