* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download The electric field
Hall effect wikipedia , lookup
Superconductivity wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Multiferroics wikipedia , lookup
Insulator (electricity) wikipedia , lookup
Electrostatic generator wikipedia , lookup
Eddy current wikipedia , lookup
Electric machine wikipedia , lookup
History of electrochemistry wikipedia , lookup
Static electricity wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Lorentz force wikipedia , lookup
Electrocommunication wikipedia , lookup
Electrical injury wikipedia , lookup
Electroactive polymers wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electromotive force wikipedia , lookup
General Electric wikipedia , lookup
Electric current wikipedia , lookup
Electric charge wikipedia , lookup
Electromagnetic field wikipedia , lookup
Faraday paradox wikipedia , lookup
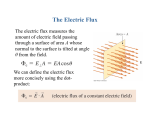
PHY114 TUTOR SESSIONS Sunday Monday Tuesday Wednesday Thursday Jiajie Xiao Hyunsu Lee Jiajie Xiao Hyunsu Lee Friday Saturday All tutorials will be in room Olin 103, 5:00 pm – 7:00pm The tutor sessions in past semesters past were successful and received high marks from many students. All students are encouraged to take advantage of this opportunity. Some private tutors may also be available through the Physics office. Chapter 24: Gauss’s Law Reading assignment: Chapter 24 Homework 24.1, due Monday, Sept. 19: OQ4, OQ5, CQ2, QQ1, 3, 4, 8, 9, 10, 12, 27, 35 Homework 24.2 due Wednesday, 21: OQ6, OQ9, QQ3, 57 • Electric flux, FE • Understand all the quantities in Gauss’s law: FE • Understand how to use Gauss’s law: E dA qinside 0 • Find total charge in a region, knowing 𝐸 outside this region. • Find total electric flux, FE out of a region when charge is known. • Calculate E-field of highly symmetric charge distributions (sphere, plate, (line)). • Deal with complicated problems using qualitative reasoning • Properties of conductors in electrostatic equilibrium Johann C. F. Gauss, 1777 – 1855 Electric flux, FE • Electric flux, FE, is the amount of electric field going through a perpendicular surface. When the surface is flat, and the fields are constant and uniform, the flux is: 𝜙𝐸 = 𝐸𝐴⊥ 𝜙𝐸 = 𝐸𝐴𝑐𝑜𝑠𝜃 𝜙𝐸 = 𝐸 ⋅ 𝐴 q is the angle between 𝑛 and 𝐸 • Good analogy: Holding a bucket in shower catching water n̂ n̂ FE A E FE 0 Electric flux, FE • When the surface is curved, or the fields are not constant, we need to use the integral definition of FE: FE E dA surface Definition of the electric flux, FE • The net flux through a closed surface is: FE E dA E n dA This is a rather abstract definition. In our applications, E is usually constant or zero over a surface, and parallel or perpendicular to a surface. Then the integral is easy to do, or becomes zero. Select a (Gaussian) surface for which this is the case. Electric flux, FE Sign of flux: - E going into a closed surface: FE is negative - E is coming out of a surface: FE is positive The net flux of a closed surface is proportional to the number of lines leaving minus number of lines entering. i-clicker 23.1 A cylindrical piece of insulating material is placed in an external electric field, as shown. The net electric flux passing through the entire surface of the cylinder is (A) Positive. (B) Negative (C) Zero. Is the answer independent of the shape of the surface? White board example 24.1 Consider a uniform electric field oriented in the xdirection in empty space. Find the net electric flux through the surface of a cube (edge length, l), placed in the field as shown in the figure. White board example 24.2 A 40 cm diameter loop is rotated in a uniform electric field until the position of maximum electric flux (through the loop) is found. The flux in this position is 5.20 x 105 Nm2/C. What is the electric field strength? “Derivation” of Gauss’s law i-clicker 23.2 Suppose a point charge is located at the center of a spherical surface. The electric field, E, on the surface and the total flux FE through the surface, are determined. Now the radius of the sphere is halved. What happens to the flux, FE , and the magnitude of the electric field, E? (A) Flux and field increase (B) Flux and field decrease (C) Flux increases, field decreases (D) Flux decreases and field increases (E) Flux remains the same and field increases Gauss’s Law • No matter what shape you use, the total electric flux out of a region containing a point charge q is 4keq = q/0. Why is this true? • Electric flux is just measuring how many field lines come out of a given region q • No matter how you distort the shape, the field lines come out somewhere F E 4 ke q FE q 0 • If you have multiple charges inside the region their effects add • However, charges outside the region do not contribute FE q1 q2 q3 0 q4 q3 FE q1 q2 qin 0 ϕE = qin E ∙ dA = ϵ0 Using Gauss’s Law Gauss’s Law can be used to solve three types of problems: 1. Finding the total charge in a region when you know the electric field outside that region 2. Finding the total flux out of a region when the charge is known a) It can also be used to find the flux out of one side in symmetrical problems b) In such cases, you must first argue from symmetry that the flux is identical through each side 3. Finding the electrical field in highly symmetrical situations a) One must first use reason to find the direction of the electric field everywhere b) Then draw a Gaussian surface over which the electric field is constant c) Use this surface to find the electric field using Gauss’s Law d) Works generally only for spherical, cylindrical, or planar-type problems S Q2 i-clicker 23.3: Q1 Which of the following statements is (are) true? (A) The electric field E at any point on the surface S is determined only by the charges inside S (Q1 and Q2). (B) The electric flux FE through surface S is determined only by the charges inside S (Q1 and Q2). (C) The field E at any point on S is determined by all the charges (Q1, Q2 and Q3). (D) The electric flux FE through S is determined by all the charges (Q1, Q2 and Q3). (E) Two of the above. Q3 Using Gauss’s Law to find E-field (charged sphere) White board example 24.3 A sphere of radius a has a total charge Q and uniform charge density throughout. What is the direction and magnitude of the electric field everywhere? • All directions are created equal in this problem (radial symmetry). • The electric field will point away from the sphere at all points. E rˆE • The electric field must depend only on the distance, r • Draw a sphere of radius r around this charge (Gauss surface). • Now use Gauss’s Law with this sphere ke Q E 2 rˆ r a Like a point charge for r > a r Is this the electric field everywhere? E Using Gauss’s Law to find E-field (charged sphere) White board example 24.3 (cont.) A insulting sphere of radius a has a total charge Q and uniform charge density throughout. What is the direction and magnitude of the electric field everywhere? • When computing the flux for a Gaussian surface, only include the electric charges inside the surface E rˆE ke Q ˆ r 2 r E keQr rˆ a3 r/a for r a, r for r a. E a Electric Field From a Line Charge White board example 24.4 What is the electric field from an infinite line with linear charge density ? n̂ E E rˆE n̂ L r • Electric field must point away from the line charge, and depends only on distance • Add a cylindrical Gaussian surface with radius r and length L • Use Gauss’s Law 2ke E rˆ r • The ends of the cylinder don’t contribute (E is perpendicular to normal) • On the curved surface, E is parallel to the normal Electric Field From a Plane Charge White board example 24.5 What is the electric field from an infinite plane with surface charge density ? E E kˆ E n̂ n̂ n̂ • Electric field points away from the surface, and depends only on distance d from the surface • Add a box shaped Gaussian surface of size 2d L W • Use Gauss’s Law • The sides don’t contribute (E-field is perpendicular to normal) • On the top and bottom, the electric field and the normal are parallel kˆ E 2 0 i-clicker 24.4 The electric charge per unit area is + for infinite plate 1 and – for infinite plate 2. The magnitude of the electric field associated with plate 1 is /(20) and the electric field lines for this plate are as shown. When the two plates are placed parallel to one another, the magnitude of the electric field is A /e0 between, 0 outside. B /e0 between, ± /(2e0) outside. (C) zero both between and outside. (D) ± /(2eo) both between and outside. (E) none of the above. Conductors in electrostatic Equilibrium Charges in a conductor are mobile. Thus, for a conductor at electrostatic equilibrium (when charges are not moving any longer) the following is true: 1. The electric field inside a good (hollow or solid) conductor is zero. If it would not be, charges would move according 𝐹 = 𝑞 ∙ 𝐸. 2. Any net charge on a good conductor distributes itself on the surface (Faraday cage). From Gauss’s law and 𝐸 = 0 inside a conductor. 3. The electric field is always perpendicular to the surface outside of a conductor. If it had a vertical component, again, charges would rearrange until there would be no more vertical component. 4. Magnitude of E-field immediately outside of 𝜎 conductor is 𝐸 = 𝜀0 5. On irregularly shaped objects, charges accumulate on location with smallest radius of curvature (sharp points). More in chapter 25. * None of the above is true for an insulator Conductors in Electrostatic Equilibrium i-clicker 24.5 Where is the safest place during a thunderstorm (to avoid being killed by lightning)? (A) Inside your car (B) Under a tree (C) On an open field Conductors in Electrostatic Equilibrium i-clicker 24.6. Where does the charge go? A hollow conducting sphere of outer radius 2 cm and inner radius 1 cm has q = +80 nC of charge put on it. What is the surface charge density on the inner surface? On the outer surface? 80 nC A) 20 nC/cm2 1 cm B) 5 nC/cm2 C) 4 nC/cm2 2 cm D) 0 E) None of the above cutaway view The electric field: • The electric field in the cavity and in the conductor is zero. • The electric field outside the conductor can be found from Gauss’s Law. E 20 nC rˆ 2 r 0 Conductors in Electrostatic Equilibrium i-clicker 24.7 Which of the following is true? (A) The electric field inside a charged insulating sphere must be zero. (B) The electric field inside a charged conducting sphere (metallic part) must be zero. (C) The charge on a conducting spherical shell will always be equally distributed on the inner and outer surface regardless of the presence of other charges in the vicinity of the shell (hint: remember induction?). (D) Two of the above (E) Three of the above Conductors in Electrostatic equilibrium White board example 24.7 A conducting spherical shell of inner radius, b, and outer radius, c, carries a net charge, -2Q. Concentric, inside the hollow shell is a solid insulating sphere of radius, a, carrying a net positive charge, Q, with uniform charge distribution, . Using Gauss’s law calculate the electric field everywhere. Exercise: Draw the field lines and the magnitude of the electric field for the following charge distributions Hollow conduction shell, with charge -2Q on it Exercise: Come up with other ‘simple geometries’ Review: • Electric flux (know what it is, how to calculate) • Gauss’s law FE E dA qinside 0 • When using to calculate electric field we can solve the integral when: 1) From geometry/symmetry find a surface over which E-field is constant 2) The dot product E dA can be simplified to E·dA, because E and A are parallel 3) Or the dot product E dA can be argued to be zero, because E and A are perpendicular 4) The electric field is zero over a portion of the surface • Field of charged sphere, line, plane • Properties of conductors in electrostatic equilibrium: i) no field inside, ii) charge resides on surface, iii) field is perpendicular on conductor surface, iv) surface charge density is greatest at sharpest points). Extra Material White board example 25.6. Consider a long cylindrical charge distribution of Radius R with a uniform charge density . Find the electric field at distance r from the axis where r < R. R r Gaussian surface L