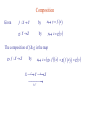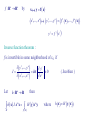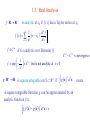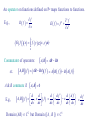Download 1._SomeBasicMathematics

Prolog
Website:
Homework submission:
•
•
•
•
•
•
http://ckw.phys.ncku.edu.tw
[email protected]
Algebra / Analysis vs Geometry
Relativity → Riemannian Geometry
Symmetry → Lie Derivatives → Lie Group → Lie Algebra
Integration → Differential forms → Homotopy, Cohomology
Tensor / Gauge Fields → Fibre Bundles
Topology
•
Hamiltonian dynamics
•
Statistics
• Electrodynamics
• Fluid Dynamics
• Thermodynamics
• Defects
Main Textbook
B.F.Schutz,
“Geometrical Methods of Mathematical Physics”, CUP (80)
Supplementary
• Y.Choquet-Bruhat et al,
“Analysis, Manifolds & Physics”, rev. ed., North Holland (82)
• H.Flanders,
“Differential Forms”, Academic Press (63)
• R.Aldrovandi, J.G.Pereira,
“An Introduction to Geometrical Physics”, World Scientific (95)
• T.Frankel,
“The Geometry of Physics”, 2nd ed., CUP (03)
Geometrical Methods of Mathematical Physics
Bernard F. Schutz,
Cambridge University Press (80)
1.
2.
3.
4.
5.
6.
Some Basic Mathematics
Differentiable Manifolds And Tensors
Lie Derivatives And Lie Groups
Differential Forms
Applications In Physics
Connections For Riemannian Manifolds
And Gauge Theories
1. Some Basic Mathematics
1.1
1.2
1.3
1.4
1.5
1.6
The Space Rn And Its Topology
Mappings
Real Analysis
Group Theory
Linear Algebra
The Algebra Of Square Matrices
See: Choquet, Chapter I.
Basic Algebraic Structures
See Choquet, Chap 1 or Aldrovandi, Math.1.
• Group ( G,  )
• Ring ( R, +,  ) : ( no e, x -1 )
• Field ( F, +,  ) : Ring with e & x-1 except for 0.
• Module ( M, +,  ; R )
• Algebra ( A, +,  ; R with e )
• Vector space ( V, + ; F )
Prototypes:
R is a field.
Rn is a vector space.
1.1. The Space Rn And Its Topology
• Goal: Extend multi-variable calculus (on En) to curved spaces
without metric.
– Bonus: vector calculus on E3 in curvilinear coordinates
• Basic calculus concepts & tools (metric built-in):
– Limit, continuity, differentiability, …
– r-ball neighborhood, δ-ε formulism, …
• Essential concept in the absence of metric:
Proximity → Topology.
Real number R = complete Archimedian ordered field.

Rn  x   x1,
, x n  xi  R
 = Set of all n-tuples of real numbers
~ Prototype of an n-D continuum
Distance function (Euclidean metric):
d : R R  R
n
n
 x, y 
d  x, y  
 x
i
y

i 2
i
(Open) Neighborhood of radius r at x :
N r  x    y d  y, x   r 
A set S is open if
x  S ,  N r  x  s.t. N r  x   S
A set S is discrete if
x  S ,  N r  x  s.t.  N r  x  \ x 
S 
Preview: Continuity of functions will be defined in terms of open sets.
Hausdorff separated: Distinct points possess disjoint neighborhoods.
A system U of subsets Ui of a set X defines a topology on X if
1.
, X  U

2.
i 1
N
3.
i 1
Ui  U
( Closure under arbitrary unions. )
Ui  U
( Closure under finite intersections. )
Elements Ui of U are called open sets.
A topological space is the minimal structure on which concepts of
neighborhood, continuity, compactness, connectedness
can be defined.
Usual topology of Rn = Topology with open balls as open sets
Metric-free version: Define Nr(x) in terms of open intervals.
Trivial topology: U = { , X }
→ every function on X is dis-continuous
Discrete topology: U = 2X
→ every function on X is continuous
Exact choice of topology is usually not very important:
2 topologies are equivalent if there exists an homeomorphism
(bi-continuous bijection) between them.
Tools for classification of topologies:
topological invariances, homology, homotopy
1.2.
Mappings
Map f from set X into set Y, denoted,
f : X Y
by
x
y  f  x
associates each xX uniquely with y = f (x) Y.
Domain of f = Domain  f   X
Range of f = Range  f   Y
Image of M under f =
f M  
 f  x
xM

Inverse image of N under f = f 1  N    x f  x   N
f 1 exists iff f is 1-1 (injective):
f is onto (surjective) if f (X) = Y.
f is a bijection if it is 1-1 onto.

f  x   f  x  x  x
Composition
Given
f : X Y
by
g :Y  Z
by
x
y
y  f  x
z  g  y
The composition of f & g is the map
g f :X Z
by
x
z   g f  x   g  f  x    g  y 
f
g
X 
 Y 
Z


g f
Continuity
Elementary calculus version:
Let f : R → R. Then f is continuous at x0 if
   0    0 s.t.
Open ball version: Let
f  x   f  x0     x  x0  

N   x0   x
x  x0  

Then f is continuous at x0 if
   0    0 s.t. f  x   N   f  x0    x  N   x0 
i.e.,
   0    0 s.t. f  N   x0    N   f  x0  
Two possible interpretations in terms of open sets:
1. Every open set in Domain( f) is mapped into an open set in
Range(f).
2. Every open set in Range( f) has an open inverse image.
Every open set in Domain( f) is mapped into an open set in
Range(f)? No!
Open M → half-closed f(M)
Every open set in Range( f) has an open inverse image? Yes.
Open N → half-closed f -1(N)
Continuity at a point:
f : X → Y is continuous at x if the inverse image of any open
neighborhood of f (x) is open, i.e., f -1(N[f(x)]) is open.
Continuity in a region:
f is continuous on M  X if f is continuous  xM, i.e.,
the inverse image of every open set in M is open.
Differentiability of f : Rn → R
f  C k if
 k f  x1 ,
 x

, xn 
j k
f  C 0 means f is continuous
exists & is continuous  j  1,
,n
f  C  means f is analytic
f : Rn  Rn
by
y  f x
x
x ,
1
, xn 
y ,
1
, yn    f 1 x ,
yj  f
j
, f n x
x 
i
Inverse function theorem :
f is invertible in some neighborhood of x0 if
J
Let
  y1 ,
x ,
1
,x
h : Rn  R
n
h
x
J
d
x



M
, yn 

f M 
n

 yi
 det
0
j
x
( Jacobian )
then
H  y d ny
where
h x  H  y x
1.3. Real Analysis
f :RR
is analytic at x0 if f (x) has a Taylor series at x0
f  x 


n0
n
1
n d f
 x  x0 
n!
d xn
x0
f  C  if f is analytic over Domain( f)
 1 
f  exp   2   C  but is not analytic at x  0
 x 
g : R n  R is square integrable on S  Rn if
C  ~ C   convergence
n
g
x
d
x



2
S
A square integrable function g can be approximated by an
analytic function f s.t.
n
f
x

g
x
d




 x

2
S
exists.
An operator on functions defined on Rn maps functions to functions.
f
D f  
x
E.g.,
3 f
E f   f  3
x
2
x
G  f    x    f  y  g  x, y  dy
0
Commutator of operators:
s.t.
 A, B  f    AB  BA f 
A & B commute if
E.g.,
 A, B  AB  BA
 A B  f   B  A f 
 A, B   0
d 
d  df
d
 A, B   f    , x   f    x
dx 
dx  dx
 dx
d d f 

df

x


 
dx
dx



dx
Domain (AB)  C2 but Domain ([A , B ])  C1
1.4. Group Theory
A group (G,  ) is a set G with an internal operation  : GG → G that
is
1. Associative:
x   y  z    x  y   z  x  y  z  x, y , z  G
2. Endowed with an identity element:
 e  G s.t. x  e  e  x  x  x  G
3. Endowed with an inverse for each element:
 x 1  G s.t. x  x 1  x 1  x  e  x  G
A group (G, +) is Abelian if all of its elements commute:
x  y  y  x  x, y  G
( Identity is denoted by 0 )
Examples:
(R,+) is an Abelian group.
The set of all permutations of n objects form the permutation group Sn.
All symmetries / transformations are members of some groups.
Rough definition:
A Lie group is a group whose elements can be continuously parametrized.
~ continuous symmetries.
(S, ) is a subgroup of group (G, ) if S  G.
E.g., The set of all even permutations is a subgroup of Sn.
But the set of all odd permutations is not a subgroup of Sn (no e).
Groups (G,) is homomorphic to (H,*) if  an onto map f : G → H s.t.
f  x  y  f  x * f  y
 x, y  G
It is an isomorphism if f is 1-1 onto.
(R+,) & (R,+) are isomorphic with f = log so that
log  x  y   log x  log y x, y R
1.5. Linear Algebra
( R,  , + ) is a ring if
1. ( R, + ) is an Abelian group.
2.  is associative & distributive wrt + , i.e.,  x,y,z R,
 x  y  z  x   y  z  x  y  z
x   y  z  x  y  x  z
 x  y  z  x  z  y  z
E.g., The set of all nn matrices is a ring under matrix multiplication & addition.
Ring ( R,  , + ) is a field if
1.  eR s.t. ex = xe = x  xR.
2.  x-1 R s.t. x-1  x = x  x-1 = e  xR except 0.
E.g., R & C are fields under algebraic multiplication & addition.
( V, + ; R ) is a module if
1. ( V, + ) is an Abelian group.
2. R is a ring.
3. The scalar multiplication RV→V by (a,v)  a v satisfies
a  v  u  av  au
 a, b  R & u, v V
 a  b v  av  bv
 ab v  a bv 
4. If R has an identity e, then ev = v  vV.
Module ( V, + ; F ) is a linear (vector) space if F is a field.
( A, , + ; R ) is an algebra over ring R if
1. ( A, , + ) is a ring.
2. ( A, + ; R ) is a module s.t.
a  v  u   a v   u  v   au
 a  R & u, v  A
We’ll only use
F = K = R or C.
For historical reasons, the term “linear algebra” denotes the study of linear
simultaneous equations, matrix algebra, & vector spaces.
Mathematical justification:
( M, , + ; K ) , where M is the set of all nn matrices, is an algebra .
Linear combination:
a v
i
i
where ai  K & vi V
i
{ vi } is linearly independent if
a v
i
0
i
 ai  0  i
i
A basis for V is a maximal linearly independent set of vectors in V.
The dimension of V is the number of elements in its basis.
An n-D space V is sometimes denoted by V n .
n
Given a basis { ei }, we have
v   v ei  v ei
i
i 1
vi are called the components of v.
i
 v V
V  span e i 
A subspace of V is a subset of V that is also a vector space.
n
Einstein’s
notation
A norm on a linear space V over field K  R or C is a mapping
n : V  R by v
n  v  v
s.t.
 u, v V & a  K
1.
n  v  u  n  v   n  u
( Triangular inequality )
2.
n a v  a n  v
( Linear )
3.
n  v  0
( Positive semi-definite )
4.
n  v  0  v  0
n is a semi- (pseudo-) norm if only 1 & 2 hold.
A normed vector space is a linear space V endowed with a norm.
Examples:
n x 
 x 
i 2
i
Euclidean norm
n  x   max
 x 
i
An inner product on a linear space (V, + ; K) is a mapping
, : V V  K by
 v, u
s.t.
 u, v, w V & a  K
1.
vu, w  v , w  u , w
2.
a v,u a v,u
3.
v,u  u,v
4.
v,v 0
5.
v,v 0  v0
v, u
or, for physicists,
v,au a v,u
*
u & v are orthogonal 
( Sesquilinear )
v, u  0
Inner Product Spaces
Inner product space  linear space endowed with an inner product.
An inner product  ,  induces a norm || || by
v 
v,v
Properties of an inner product space:
1.
v, u  v u
( Cauchy-Schwarz inequality )
2.
vu  v  u
( Triangular inequality )
3.
vu  vu  2 v  u
2
2

2
2

( Parallelogram rule )
The parallelogram rule can be derived from the cosine rule :
v  u  v  u  2 v u cos 
2
2
2
v  u  v  u  2 v u cos    
2
2
2
( θ  angle between u & v )
1.6 .
The Algebra of Square Matrices
T : V V
T : V V
T : V V
 a, b  K & v, uT:VV  V
A linear transformation T on vector space (V, + ; K) is a map
s.t.
T  a v  bu  a T  v   b T  u
If { ei } is a basis of V, then
x  x iei

Setting T  ei   e j T j i

Tx 
j
 T ji xi
i
T  x   T  x i e i   x T  ei 
we have
T  x   xi e j T j i   Tx  j e j
T ji = (j,i)-element of matrix T
Writing vectors as a column matrix, we have
T x  T  x
(  = matrix multiplication )
In linear algebra, linear operators are associative, then
k
j i
AB  x   A  B  x    A  e j B j i x i   ek A j B i x
  AB  x   e k  AB  k x i
i
 AB  i  Ak j B j i

k
Similarly,

~
AB  A  B

A B  C  x     AB   C  x    A   BC  x  
~
A   B   C  x     A  B    C  x   A    B  C  x 
i.e., linear associative operators can be represented by matrices.
We’ll henceforth drop the symbol 
In general:
AB  BA
Transpose:
A 
Adjoint:
A
T i
Unit matrix:

j
 A ji
j
 A j i*
 i
I j   i j
i
A1A  AA1  I
Inverse:
A is non-singular if A-1 exists.
The set of all non-singular nn matrices forms the group GL(n,K).
Determinant:
i
1
in
det A   i1
in
ai11
ain n
i1 in is an even permutation of 1 n
1

  1 if i1 in is an odd permutation of 1 n
0
otherwise

Cofactor: cof(Aij) = (-)i+j  determinant of submatrix obtained
by deleting the i-th row & j-th column of A.
det A   Ai j cof  Ai j 
Laplace expansion:
A
i
j
cof  Ai k    j k det A
j arbitrary
i
See T.M.Apostol, “Linear Algebra” , Chap 5, for proof.
i

Trace:
A 
1 i
j

cof  A j i 
det A
TrA  A i i
Similarity transform of A by non-singular B:
A  B 1 AB
~
A  B1AB
Det & Tr are invariant under a similarity transform:
det  B 1AB   det A
Tr  B 1AB   TrA
Miscellaneous formulae
 AB   BT AT
 AB   B 1A 1
1
T
det  AB   det A   det B
det AT  det A
λ is an eigenvalue of A if  v  0 s.t.
A v   v
~
Av v
v is then called the eigenvector belonging to λ.
For an n-D space, λ satifies the secular equation:
det A   I  0
There are always n complex eigenvalues and m eigenvectors with m  n.
det A    i
TrA    i
i
Eigenvalues of A & AT are the same.
i