Download H 1

Assumptions of perfect competition
1- Homogeneous product
2- consumers are identical from seller’s point of view
3- Both firms and consumers are numerous.
4- Both firms and consumers have perfect information about the market.
5- Entry and exit are free without any serious barrier
Violation of any of the above assumption will lead to emergence of
monopoly. For example ;
By assumption 1 we do not have trademarks or patents , special brand ,
so on. The entrepreneurs will sell to the highest bid.
By assumption 3 ,neither the change in the production level of individual
firms, nor a change in the consumption level of individual consumer
could affect the price level. Consumers and producers are price
takers. This is the most important feature of perfect competition
conditions. Any level of market power to influence the price
level is not accepted by this condition.
H&Q,
CH 6
Market Equilbrium
1
Assumptions of perfect competition
By assumption 4 , a single price must prevail in the market. Having
more than one price for a single commodity with the same quality is
not accepted.
So in such a situation;
Consumers are maximizing their utility given the income level and
commodity prices.
Producers are maximizing profit , given the cost of production and
input prices.
Consumers are demanding in the commodity market and supplying
their inputs in the factor market. While producers are demanding
inputs in the factor markets and supplying in the commodity market.
Neither any consumer , nor any individual could affect the price level.
But the action of all of the consumers or all of the producers could
affect the market price level .
H&Q,
CH 6
Market Equilbrium
2
Assumptions of perfect competition
In the following figure , we could see the function of a perfectly
competitive market.
P
MCi
D=Σjdj
S=ΣjMCi
dj =f(pj,mj)
ACi
MR=P
qi
qi0
Demand for each firm’s product
P0
P0
Q
Q0
Q0=Σiqi0 =Σjqj0
qj
qj0
Supply which each individual faces
Market clears because of working the market mechanism (invisible hand)
H&Q,
CH 6
Market Equilbrium
3
Production periods (perfect competition)
We can specify production periods into three categories; very short-run ,
short-run , long-run. Demand function of individuals in any of these
categories is downward sloping and is a function of it’s own price, other
prices and income level. But the shape and nature of the supply function
differs concerning the length of the period.
1-very short-run
Supply can not be increased or decreased. All the supply should be sold out
any how. Like the fisher man who should sell all the fishes by the end of the
day. Or the winter cloth which should be sold by the end of the winter. Or
the annually wheat production which should be sold by the end of the year,
because it should not be stored.
Because of competition, Increase
Very short-run supply
S=MC
or decrease in demand will
be followed by increase(decrease) P*
in price level . Price is a demand
D
D’
Price and supply does not have any
Role in price determination.
*
H&Q,
CH 6
P1
Market Equilbrium
4
Production periods (perfect competition)
2- Short-run
In short-run supply can be changed, but scale of production can not. At
least ,one of the inputs(capital) is fixed and this will limit the change in
production level.
P,C
SMCi
SAVCi
Pm=Min AVC
Si=SMCi(p)
P≥min SAVC
Si=0
P<min SAVC
Market supply=S=Σisi(p)
qm
H&Q,
CH 6
qi
Market Equilbrium
5
Production periods (perfect competition)
3- Long-run
In long-run all the inputs can change . So scale of production can vary and
be adjusted to an optimum level. The long-run marginal cost of a firm is it’s
long-run supply , but the long-run supply of industry is not the summation
of the firm’s individual marginal cost curve . The Shape of industry long-run
supply curve depends upon the presence of the external economies or
diseconomies.
When there are new entry into the industry , the production level in the
industry will increase, Qindustry
When Qindustry
Pinput
external diseconomies
Pinput
external economies
1- External diseconomies;
Dinputs
Pinputs
Tci
Mci
Poutput
2- External economies;
sometimes when production in industry level increases , better trained
and more efficient use of labor is economical and possible . For this reason
H&Q,
CH 6
Market Equilbrium
6
Production periods (perfect competition)
Total cost of production for producing a specific amount of output will
decrease. This will lead to decrease in the marginal cost of production and
decrease in price of output.
Taking in to account the externalities , solving the following equations will
give the market supply equation;
Q=Σinqi
Ci = Φ(qi,Q)
Πi = TRi – TCi
i = 1,2,3…n
dΠi/dqi = p - dΦ(qi,Q)/dqi = 0
n equations , n unknowns , qi=si(p)=individual supply
Market supply = SM(p)=Σin si(p)
d SM(p)/dp >0
external diseconomies
(min of LAC shifts up)
d SM(p)/dp <0
external economies
(min of LAC shifts down)
d SM(p)/dp =0
No externality
(min of LAC stays at the
previous price level)
H&Q,
CH 6
Market Equilbrium
7
Commodity market equilibrium(perfect competition)
1- Short-run equilibrium;
In a perfectly competitive situation, the action of auctioneer and contracting
and re-contracting process , equilibrium will be attained.
When there is excess demand, (D>S), biding up the price level by
consumers will force the price level to increase. Increase in price level will
encourage the sellers to increase their supply of product to the market. This
process will continue till excess demand disappears and market clears.
When there is excess supply , (S>D), sellers are competing to sell their
products to the limited customers, so they try to reduce their price level to
get a bigger share of the market. Reducing the price will force them to
supply less amount of product to the market. This process will continue till
excess supply disappears and market clears.
At the equilibrium price level , neither the seller nor the buyer is willing to
recontract any further.
H&Q,
CH 6
Market Equilbrium
8
Commodity market equilibrium(perfect competition)
2- long run equilibrium;
Intersection of long-run supply curve with the corresponding demand curve forms
the long-run equilibrium.
long-run cost includes normal profit.
Normal profit is minimum necessary for the firm to remain in existence. In other
words total revenue is enough for managerial services , risk bearing ,
organizational provision, etc.
P
If Pe is such that industry earns more than
LS
Normal profit , firms will enter to industry,
Pe
Supply shifts to the right, pe will decrease,
D
Excess profit will disappear.
S(P)=nSi(P)
Q
D(p)=S(P)
Qe
Πi=Tri – LTCi =0
PSi(P) – Φ[Si(p)]=0
qi=Si(P)=S(P)/n
Solving the above equations in long run will give number of firms and equilibrium
demand, supply, and price level.
H&Q,
CH 6
Market Equilbrium
9
Commodity market equilibrium(perfect competition)
We could see the Long run equilibrium in the following figure.
P
LMCi
P’
2
Excess profit
S=S(P)
1
2
LACi
1
Pe
Pe
S’=S’(P)
LS
D’=D’(P)
D=D(P)
qi0
qi’
qi
Q0 =Σin qi0
Q1 =Σin’ qi0
n’>n
Constant cost industry with no externality
H&Q,
CH 6
Market Equilbrium
10
Commodity market equilibrium(perfect competition)
Differential cost condition and rent;
The symmetric assumption of the firms makes the analyses convenient , but
it may not be necessary in the Long-run. Firms may differ with respect to
the plant size, scare factor, organization ability, etc.
If one firm or a group of firms could produce with lower cost such as those
shown in Figure a . The earned profit in this way could be interpreted as
the rent of the factors of production or input which is causing the cost of
production to decrease. This rent (or excess profit) could be claimed by the
said factor as increase in its wage in the log-run.
Rent=excess(pure) profit
P
MC2
pe
MC1
P
AC1
AC2
pe
P
S
pe
D
q2
H&Q,
CH 6
q1
Market Equilbrium
Q=q1+q2
11
Commodity market equilibrium(perfect competition)
An application to taxation;
Ci=Φ(qi)+bi
Tax rate = t per unit of production (sale)
Ci= Φ(qi)+bi + tqi
MCi= Φ’(qi) + t
MCi = P , Φ’(qi) + t =P , qsi=qsi(p – t) = individual supply of the firm
S=Σin qsi(p – t) = Qs(P – t) = market supply
S=Qs(p – t )
S=Qs(p)
By imposing the tax, supply shifts to left;
P
If t=vp ,
c
Ci= Φ(qi)+bi + vpqi
Tax rate
Pe
MCi= Φ’(qi) + vp
b
s
s
MCi = P , Φ’(qi) + vp =P, q i=q i [p(1-v)]
a
S=Σin qsi [p(1-v)] = Qs [P(1-v)]
qe
H&Q,
CH 6
Market Equilbrium
12
Commodity market equilibrium(perfect competition)
An application to taxation;
Suppose that ; Ci=0.1qi2 +qi +10
MCi = 0.2 q +1 , MCi= P , qsi= 5p-5 if p≥min avc(=1) and qsi=0 if p<1
If n=100, market supply=S=Σin qis = 500p – 500 , if p≥1 and S=0 if p<1
If D=4000 – 400 p ,
D=S , 4000 – 400 p = 500p – 500 , then pe=5 , qe=2000
If t=tax rate = t per unit of output,
Ci=0.1qi2 +(1+t)qi +10
MCi = 0.2 q+1+t , MCi= P, qsi= 5(p-t)-5 if p≥min avc(=1+t) and qsi=0 if
p<1+t
If n=100, market supply=S=Σin qis = 500(p-t) – 500 , if p≥1+t and S=0 if
p<1+t
D=4000 – 400 p = S= 500(p-t) – 500
pe=5 + (5/9)t
(5/9)t = consumer burden=increase in the market price =bc
t - (5/9)t = (4/9)t = producer burden = decrease in price received by
producer=ab
H&Q,
CH 6
Market Equilbrium
13
Factor Market Equilibrium
Perfectly competitive factor market;
The Factor is homogeneous,
Buyers and sellers are numerous
Buyers and sellers does have perfect information
Free exit and entry is available into and from the market.
Demand function for inputs could be derived from the production function
on the assumption of profit maximization. That is ;
price of input (Pi) = value of marginal product of input i (VMPi) , but
derivation of supply function for input depends whether the input is
primary or produced input.
If the input is a produced one, supply could be derived from the marginal
cost by equating it to price level.
If input is a primary one , the specific procedure should be defined. For
example the utility maximization approach could be used to derive the labor
supply, which is called the labor-leisure choice model , or the time allocation
model
H&Q,
CH 6
Market Equilbrium
14
Factor Market Equilibrium
labor-leisure choice model;
W+H=T
(T=24)
W= working time , H=leisure time
U = g(H , Y )= U[(T-W) ,Y]
Y = labor income = Wr
Wr + Hr = Tr
r= wage rate per hour
Max U= g(H , Y )
S.T. Y + Hr = Tr
U*= g(H , Y ) + λ [Tr-(Y + Hr)]
∂U*/∂H = 0
H=H(r )
W=W(r)
supply function
∂U*/∂Y =0
∂U*/∂λ =0
As it is found from the supply function, working time is a function of wage
rate. As it is expected the supply function has positive slope, but in some
special case it has negative slope.
In order to find out the reason we have to analyze the substitution and
income effects of change in the wage rate.
H&Q,
CH 6
Market Equilbrium
15
Factor Market Equilibrium
Substitution and income effect of change in wage rate , r ,
Downward sloping supply curve
(HH2 < H2H1)
Y=Wr
Upward sloping supply curve
(HH2 > H2H1)
(24-H1)r1 = Y1
H=0 , W=T=24
H=T=24, w=0
U1
Y=0
Y=24r
U
(24-H)r=Y
r
H2H1=income effect(increase in income,
increase in leisure)
H2
H1 H
r1
H
r1 > r
HH1=total effect ,(increase in wage, decrease in leisure,
HH2 =substitution effect (increase in wage,
increase in working time)
decrease in leisure)
H & Q , CH 6
Market Equilbrium
16
The Existence and Stability of Equilibrium
1-Existence;
Demand and supply curve should have at least one point in common. Three
situation in which the supply and demand curves have no point in common
are pictured as following;
P
P
S
D
P
S
S
D
D
q
q
q
Free goods
Solid gold school lunch box
Even if P=0, S>D
Even if q=0 , Psupply>Pdemand ,
mis-specification error
What producers are willing
to receive is always greater
than what consumers are
willing to pay.
H&Q,
CH 6
Market Equilbrium
17
The Existence and Stability of Equilibrium
Uniqueness;
Most of the time it is possible for more than one equilibrium to exist.
Backward bending supply curve is an example.
P
B FIG 1
P
D S
P
FIG 2
E
S
B
D
FIG 3
S
p1
C
A
D
p2
A
q
q
Uniqueness condition;
q
1-[D’(p) – S’(p)]= δ <0 around the equilibrium price (p0)
2- if at P0, δ <0 , then ; at any P> P0 , D<S , and at at any P < P0 , D>S .
None of the above figures satisfies the two conditions for unique equilibrium. So we will have
multiple equilibrium price levels. Ignoring the equilibrium points at which δ=0, the sign of δ
must alternate in multiple equilibrium price. At point A in figure 1 , δ is negative. But at point B
, δ is positive. The same is true for figure 2 .Point C in figure 2 is semi-equilibrium point. In
figure 3 we will have a range of equilibrium points.
H&Q,
CH 6
Market Equilbrium
18
The Existence and Stability of Equilibrium
2- The Stability of Equilibrium
Existence of an equilibrium does not guarantee that it will be attained. There is no
reason to assume that the initial price will happen to be the equilibrium price.
Stable equilibrium ; disturbance result in a return to equilibrium.
Unstable equilibrium ; disturbance does not result in a return to equilibrium.
Static stability ;
Static analysis abstract from the time path of the adjustment process and considers
only the nature of the change. We will work with the Walrasian stability condition
which price level is considered as a means of adjustment.
E(P) = D(P) – S(P)
dE(P)/dp = E’(P)= D’(P) – S’(P)<0
If S(P) & D(P) are both positively sloped, supply should be flatter than demand.
If S(P) & D(P) are both negatively sloped, demand should be flatter than supply.
Point A in FIG 1 and 2 is stable since E’(P) is negative. Point B in Figure 1 and 2 is
not stable, since E’(P) is positive in point B . Point C is semi-stable . These
conditions are not enough for determining about the dynamic stability of the point.
H&Q,
CH 6
Market Equilbrium
19
The Existence and Stability of Equilibrium
Dynamic stability;
Suppose that , we proved the existence of equilibrium and found out that it
will finally be attained. But , one might not expect instantaneous
adjustments in the present model.
The dynamic nature of the re-contracting may be formulized in a model in
which re-contracting takes place during periods of fixed length, with the
auctioneer announcing the new prices at the beginning of each period.
Equilibrium is stable if prices converge to the equilibrium over time.
Suppose that positive excess demand would raise the price level over time
according to the following relation.
Pt – Pt-1 = k E(Pt-1)
k>0 , E(Pt-1)= excess demand in period t-1
Suppose ; Dt=aPt + b
St=Apt + B
(Pt – Pt-1)/k = E(Pt-1) = (a – A)Pt-1 + b – B
Pt= [1+k(a – A)]Pt-1 + k (b – B) first order difference equation
solving the equation will give the following solution;
H&Q,
CH 6
Market Equilbrium
20
The Existence and Stability of Equilibrium
Pt=(Po – Pe)[1+k(a – A)]t + Pe
Po = initial price at t=to
Pe=(b-B)/(A-a) = equilibrium price when
Dt=St
for stability condition Pt should converge to Pe over time. That is ;
if , 0<[1+k(a – A)]<1 , when t converges to infinity, Pt converges to Pe
without oscillation.
[1+k(a – A)]<1 , k(a – A)<0 , k>0 , (a – A)<0 , static stability condition,
0<[1+k(a – A)] , -1 <k(a – A) , k>-1/(a-A) ,
k>1/(A-a)
As it could be seen from the above formula, for maintaining the dynamic
stability condition ,not only the static stability condition should be
maintained but also the magnitude of k should be greater than some
minimum amount. In other words the dynamic stability condition depends
on k which indicates that the extent to which the market adjust.
As it is clear, the dynamic stability condition implies the static condition ,
but the reverse is not true.
H&Q,
CH 6
Market Equilbrium
21
The Existence and Stability of Equilibrium
In the following figures we could show that how the magnitude of
k influence the length of adjustment.
Pt
Pt=Pt-1
Pt=Pt-1=Pe
Pt=Pt-1 + k E(Pt-1)
P3
P2
P1
Larger K will lead to increase the
speed of adjustment and fewer
periods of adjustment.
Pt-1
Po
H&Q,
P1
CH 6
P2
Market Equilbrium
22
The Existence and Stability of Equilibrium
Dynamic Stability with Continuous Adjustment
Adjustment may take place continuously rather than in discrete time
intervals. The condition for dynamic stability becomes;
( dp/dt )= k E(P)
E(P)t=Dt – St= (aPt+b) – (Apt + B)
dp/dt = k(a – A)pt +k(b – B) first order differential equation
solution : Pt=(Po – Pe)ek(a-A)t + pe
If (a – A)<0 , P tends to Pe when t tends to infinity
Local Stability ;
An equilibrium point is locally stable if the system returns to it , given a
small initial deviation from the equilibrium.
Global Stability;
An equilibrium is global stable if system returns to it for any initial
deviation from equilibrium.
Linear models are both locally and globally stable if they are stable.
In order to make models globally stable,linear approximation is used for
non-linear models.
H&Q,
CH 6
Market Equilbrium
23
Dynamic Equilibrium with lagged adjustment
Production takes time, so adjustment may not be instantaneous.
In some markets like Agricultural products, supply responds to last year
price level , while demand respond to the current year price level.
Dt=aPt + b
St=Apt-1 + B
equilibrium price = Pe=(B – b)/(a – A), where Dt=St ,(Pt=Pt-1=Pe)
As St appears in the market , Pt makes it equal to Dt. In equilibrium no
producers is left with unsold stocks, and no consumers left with
unsatisfied demand.
Dt =St
aPt + b – Apt-1 – B =0
Pt= (A/a)Pt-1 + (B – b)/a
Pt=(P0 – Pe)(A/a)t + Pe
Dynamic stability condition; Pt tends to Pe when t tends to infinity.
|A/a| < 1 or |1/a| (slope of demand) < |1/A| ( slope of supply )
If |A/a| < 1 and the slope of demand and supply have opposite sign price
will oscillate and the oscillation will decrease in amplitude and it is
dynamically stable ( Fig a). If |A/a| > 1 the oscillation will increase in
amplitude and it is not stable (Fig b).
If |A/a| < 1 and the slope of demand and supply have same sign ,price
will not oscillate and it is dynamically stable (FIG c)
H&Q,
CH 6
Market Equilbrium
24
Dynamic Equilibrium with lagged adjustment
1- when demand and supply have different sign in slopes;
P
S
S
D
Po
S
P2
Po
P1
Po
P1
D
D
P1
qo
q2 q1
FIG A
q
q2
qo
FIG B
q1
qo q1
FIG C
Excess demand is zero in this COBB-WEB model.
H&Q,
CH 6
Market Equilbrium
25
Future Markets
Buyers and sellers agree to transact at a specified price at a future date. In agricultural
commodity markets, risk-averse farmer can avoid price uncertainty by selling the product
in the future market.
People who buy and sell for these reasons are said to hedge against price uncertainty. Such a
person will participate in the future market if he can increase his expected utility by
buying and selling in the Lottery offered by the market.
Expectations are identical for all individuals ; every one expects
p1 …pn with the
probability v1…..vn . All buyers and sellers are risk-averse though not by the same degree
and obey Von-Neumann Morgenstern axioms.
Suppose that a farmer is producing q with the cost function C(q) which is strictly convex. The
farmer has a utility function in the form of U(Π) which is strictly concave.
1- If the farmer sells in the future market at the going price P* , he maximizes utility by
equating this price to marginal cost.
P* = MC(q) , q=q* , U*=U[p* q* - C(q*)] ,
since p=f(q) , U*=V(P*)
2- if he does not sell in the future market , the first order condition for expected utility
maximization is :dE[U(Π)]/dq = Σin vi U’(Πi)[Pi – C’(q)]=0 → q=q0 , U0
If U0>U* , then farmer will not sell in the future market.
If U0 < U* , then farmer will sell in the future market.
Suppose that at Po* , U0 = U* ,
If P* > Po* , U0 < U* , then farmer will sell in the future market
If P* < Po* , U0 > U* , then farmer will not sell in the future market
H&Q,
CH 6
Market Equilbrium
26
Risk- assumption
Suppose that A denotes the asset position of an individual, with A0
denoting the initial position of the asset.
U0=U(A0) is the initial level of utility for the individual.
D is the excess demand in the future market. D>0 means the
individual is buying for the future delivery. D<0 means the
individual is selling for the future delivery.
Pi is the price of asset in time t=ti . P* is the price which is agreed
upon in time t=t0 .
Ai is the total value of the asset in time t=ti . The individual is trying to
maximize his expected utility ;
max E[U(A)]=Σin vi U[Ai]
S.T. Ai =A0 + (Pi – P*)D
{dE[U(A)]/dD}= Σin vi U’[Ai](Pi – P*)=0
D=D* ,
D*=D(p*)
if p* = p*0 , D(p*)=0 , then ;
for p* > p*0 , D(p*)>0 he will be net buyer for the future market
for p* < p*0 , D(p*)<0 he will be net seller for the future market
H&Q,
CH 6
Market Equilbrium
27
Problems , H & Q , CH 6
6-1 two hundred consumers derive utility from the consumption of two
goods.each has the utility function U = 10 q1 + 5q2 + 1q2. Each has a
fixed income of 100 dollars. Assume that the price of q2 is 4 dollars per
unit. Express the aggregate demand for Q1 as a function of P1. Is the
aggregate demand curve downward sloping.
Solution; Max U = 10q1+5q2+q1q2
S.T. 100 = 4q2 + p1q1
L= 10q1+5q2+q1q2 + λ[100 - 4q2 + p1q1 ]
∂L/∂q1 = 10 + q2 – λp1 =0
∂L/∂q2 = 5 + q1 – 4λ =0
∂L/∂λ = 100 - 4q2 + p1q1 =0
q1= 70/p1 – 2.5
Q1= 200q1 = 14000/p1 – 500
dQ1/dp1 = -p12/14000 <0
6-2 construct a short-run supply function for an entrepreneur whose short
run cost function is C=0.04q3 - 0.8q2 +10q1 + 5
Solution ;
P=MC
MC=0.12 q2 – 1.6q + 10 =p
H&Q,
CH 6
Market Equilbrium
28
Problems , H & Q , CH 6
Min AVC = Min (TC/q)= Min(0.04q2 – 0.8q +10)
q=10
If q=10 , p= 0.12 q2 – 1.6q + 10 =6
If p≥6 , q ≥ 10
, if P<6 , q=0
6-3 A good Q is produced using only one input x . The market for Q is
supplied by 100 identical competitive firms each of which has the
production function q=xb . Where 0<b<1 . Each firm behaves as if the
price of x were constant. However , the industry as a whole faces an
upward sloping supply curve for X as r=b(100x) where b>0. Derive the
industry long-run supply curve.
Solution ;
r=b(100x)=b(100 q1/b)
[q=xb
x=q1/b ]
TC=rx= b(100 q1/b) q1/b
MC=P , MC=(200/b)bq(2-b)/b = P
qi= [(bP)/200b]b/(2-b)
S=100 qi
6-4 The long run cost function for each firm that supplies Q is C=q3– 4q2 + 8q
Firms will enter the industry if profits are positive and leave the industry if
profits are negative. Describe the industry’s Long run supply function.
Assume that the corresponding demand function is D=2000 – 100p.
Determine the equilibrium price , aggregate quantity, and number of
firms.
H&Q,
CH 6
Market Equilbrium
29
Problems , H & Q , CH 6
Solution;
TC=q3-4q2+8q
AVC=q2-4q+8
d( AVC)/dq=0, 2q-4=0 , qi=2 , AVC=4
Constant cost industry; p=4 →LS
D=2000-100p , p=4 , D=Q=1600
Q=Σinqi , qi=2
, n=800
H&Q,
CH 6
Market Equilbrium
30
Problems , H & Q , CH 6
6-5 consider an industry with n identical firms in which the ith firm’s total
cost function is Ci=aqi2 `+ bqiq` (i=1,2,3,…..n) .where
q=q1+q2+…..qn . Derive the industry supply function.
Solution ;
Πi = Tri - Ci = pqi - aqi2 -` bqiq
(∂Πi/∂qi)= P – 2aqi – bq -bqi =0
qi= (p – bq)/(2a+b)
q= Σin qi = Σin (p – bq)/(2a+b) = (np - b Σin q )/(2a+b) =
(np – bnq )/(2a+b)
q=np/(2a +nb +b)
6-6 – Construct an effective supply curve for an industry which has two
sources of supply:domestic production with the supply curve S=20 +
8p. And 2- an unlimited supply of imports at a fixed price of 20.
Solution ;
p
Domestic supply
Supply of imports
20
180
H&Q,
CH 6
20
Market Equilbrium
q
31
Problems , H & Q , CH 6
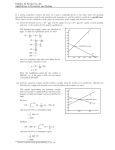
6-7 ;Determine equilibrium price and quantity for a market with the
following demand and supply functions; D = 20 – 2p and
S=40-6p. Assume that a specific tax of 1 dollar per unit is
imposed. Compute the changes in price and quantity.
Solution ;
D =S
20 - 2p = 40 – 6p , p=5 , D = S = 10 .
if tax rate =1 , then ; S = 40 – 6(p –1)
D= 20 – 2p
S=D , p=6.5, D=S=7
P
D= 20 – 2p
6.5
6
Tax = 1
5
S = 40 – 6(p –1)
10
H&Q,
CH 6
4
7
20
Market Equilbrium
S=40 – 6p
q
32
Problems , H & Q , CH 6
6-8; Assume fifty firms supply commodity Q at location I and fifty
at location II. The cost of producing output qi for the ith firm in
either location is 0.5qi2 . The cost of transporting the commodity
to the market from location I is 6 dollars per unit, and location
II , 10 dollars per unit. Determine the aggregate supply
function.
Ci = 0.5 qi2 + 6qi
MCi =qi+6=p
qi=p-6 , qi=0, p≤6
Cii = 0.5 qi2 + 10qi MCii =qi+10=p
qi=p-10
qi=0, p≤10
S=50(p-6)+50(p-10)=100p-800 aggregate supply
P
P
10
MCI
10
P
MCII
MCI +MCII =S
6
H&Q,
4
q
CH 6
4
Market Equilbrium
q
q
33
Problems , H & Q , CH 6
6-9 ; A consumer allocates a fixed amount of time to labor and
leisure. He derives satisfaction from the time he retains as
leisure, and income , y , that he secures by selling the labor at a
fixed wage rate. His utility function is U=Ly + aL where a is a
positive parameter. Derive the consumer’s supply function for
labor. Is his labor supply curve upward sloping.
T=W + L , W = T – L ,
Y=rW = r(T – L)
r= wage rate
U=LY + aL = L r (T – L )+ aL = -rL2 +(a + Tr)L
dU/dL = 0 , a + Tr –2 r L = 0
L=(a+Tr)/(2r)
W = T – L = T - (a+Tr)/2r = T/2 – a/(2r)
dW/dr = a/2r2 >0
6-10 ; Assume that aggregate demand and supply function are
given by D=25/p and S=(5p)1/2 . Is this dynamic process is
locally stable.
dp/dt = kE(p)
Pt=(po – pe)ek(a-A)t + Pe
Stability condition ; (a –A)<0 , a=-25/p2 , A=(1/2)51/2p-1/2
H&Q,
CH 6
Market Equilbrium
34
Problems , H & Q , CH 6
6-11 ; determine whether the equilibrium solution exist for markets with
the following demand and supply function.
D=12-3p , S=-10+2p,
P
Equilibrium does not exist
S
4
D
q
12
D=16 –2p , S = 20 – 2p
slopes are the same and equal to –2 . They are parallel . Equilibrium does
not exist.
D = 50 – 4p , S = 10 +10p – p2
S =D , p2-4p+48=0 , (p-4)(p-10)=0
H&Q,
CH 6
p=4 , 10
Market Equilbrium
q= 34, 10
35
Problems , H & Q , CH 6
6-12 ; Consider the following markets which are characterized by lagged
supply response :
Determine the equilibrium price and quantity for each market . Assume an
initial price 20 percent below the equilibrium price for each market, and
determine the number of periods necessary for each price to adjust to
within 1 percent of equilibrium.
(a) - Dt=40 – 10 pt ; St=2+9pt-1
(b) - Dt=30 – 5 pt ; St=20 - pt-1
Solution ;
Dt=apt+b
St=Apt-1 + B
Equilibrium ; pt = pt-1=pe , pe=(B-b)/(a-A) , p0=0.8pe
pt=(p0-pe)(A/a)t + pe = (-0.2pe)(A/a)t + pe=pe[1-0.2(A/a)t]
0.99pe ≤ pt ≤ 1.01pe ,
Dt=40 – 10 pt ; St=2+9pt-1 , , pt=[1-0.2(-9/10)t]pe ,, pe=2
-0.05 ≤ (-0.9)t ≤ 0.05
t=29
b- Dt=30 – 5 pt ; St=20 - pt-1
(0.2)t ≤ 0.05
t=2
H&Q,
CH 6
Market Equilbrium
36
Problems , H & Q , CH 6
6-13 ; A sugar refiner has a strictly concave production function for
which labor (L) and raw sugar (x) cane are the only inputs. His
production of refined sugar (qs) and purchase of inputs will
take place next spring, but he must determine his future
production level (qS) today.The future prices of refined sugar
(ps) and labor are (pL) known with certainty, but the price of
raw sugar will assume one of the values (r1, r2 ……rn) , with
the respective probabilities (v1 , v2 ,…..vn). Show how you
would determine his futures-market raw sugar demand.
Π=psqs – C
C= pLL + rix
qs=qs(L , x)
Πi=psqs – (pLL + xri)
EU(Πi)= Σin vi U(Πi)
d[ EU(Πi)]/dx =d Σin vi U(Πi)/dx = Σin vi U’(Πi)[ps ∂qs/∂x – ri]=0
Σin vi U’(Πi)( VMPx – ri )=0
Risk-neutral , U’(Πi) = α , Σin vi ( VMPx – ri )=0 , q=q0 , x=x0
Risk-averse , U’(Πi) = downward , Σin vi U’(Πi) ( VMPx – ri )=0 ,
VMPx should be rising, MPx is downward sloping , q<q0
Risk-lover , U’(Πi) = upward , Σin vi U’(Πi) ( VMPx – ri )=0 , VMPx
should be falling, MPx is downward sloping , q > q0
H&Q,
CH 6
Market Equilbrium
37