Download Graphs, Linear Equations, and Inequalities in Two Variables

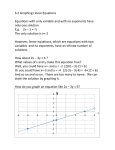
MAT 100
Armstrong/Pierson
Graphs, Linear Equations, and Inequalities in Two Variables; Functions
Unit 3
Unit Planner
____
3.1
Graphing Using the Rectangular Coordinate System
Read pages 212-217
p. 218-222
____
3.2
Equations Containing Two Variables
Read pages 222-231
p. 231-236
____
3.3
Graphing Linear Equations
Read pages 236-244
p. 244-248
____
3.4
Rate of Change and the Slope of a Line
Read pages 249-258
p. 258-263
____
3.5
Slope-Intercept Form
Read pages 263-267
p. 267-271
____
3.6
Point-Slope Form; Writing Equations
Read pages 271-276
p. 277-280
____
3.7
Graphing Linear Inequalities
Read pages 280-286
p. 287-291
____
3.8
Functions
Read pages 291-299
p. 300-303
____
Test Review
Read pages305-314
p.
____
Practice Test
____
Unit 3 Test
Cumulative Review Page 208-209 #1-50 (due two days after test)
NOTES:
Unit 3 – Graphs, Linear Equations, and Inequalities in Two Variables; Functions
3.1 – Graphing using the Rectangular Coordinate System
Review of graphing points:
Plot each point then state the
quadrant in which the point lies.
(4, -5)
(-2, -5/2)
(4, 0)
Open your book to page 216-217.
Using the line graph in the middle of the page, answer the following questions.
1. How many people were in the audience 80 minutes after taping began?
2. At what time before taping there there exactly 150 people in the audience?
3. If the x-axis represents time, why are there negative numbers on the scale?
Using the step graph in the middle of the page, answer the following questions.
1. Find the cost of renting the trailer for six days.
2. Find the cost of renting the trailer for 2 ½ days.
3. How long can you rent the trailer for $70?
4. Why are there open circles on a step graph?
When reading your assignment, define the words, label the graph, and answer the questions provided:
Define each word and label on graph.
x-axis:
y-axis:
origin:
quadrant:
coordinate:
ordered pair:
1. What is a Cartesian Coordinate System?
2. Explain the difference between a line graph and a step graph.
3. Are there any vocabulary words that you did not understand? Are there any questions you need to ask?
Unit 3 – Graphs, Linear Equations, and Inequalities in Two Variables; Functions
3.2 – Equations Containing Two Variables
What is the difference between a one-variable and a two-variable equation? Give an example of each.
1. Is (-5, -4) a solution of the equation y = x – 1. Why or why not?
2. Complete the solution (2, __) of the equation y = 2x – 4.
3. Graph y = -x + 2.
What type of graph is formed?
What type of equation is this?
4. Graph y = x2 and y = x2 + 3. Compare the graphs. What do you notice?
(Find the axis of symmetry to create tables). What is the turning point?
What type of graphs are formed?
What type of equations are they?
5. Graph y = │x│ and y = │x│ – 2. Compare the graphs. What do you notice?
(Use (0,0) as the middle of your chart).
What type of graphs are formed?
What type of equations are they?
6. Graph y = x3 and y = (x + 1)3. Compare the graphs. What do you notice?
(Use (0,0) as the middle of your table).
When reading your assignment, find the definition to the words:
Input Value:
Output Value:
Independent Variable:
Dependent Variable:
Unit 3 – Graphs, Linear Equations, and Inequalities in Two Variables; Functions
7. – Graphing Linear Equations
STANDARD FORM : Ax + By = C
1. Put the following equation in standard (general) form with no fractional coefficients:
y=½x+2
2. Which of the following are linear equations and which are non-linear?
y = 2x + 3
3x = -y + 7
y = │x│ + 3
3. Complete the table of solutions for 2x – 5y = 10
x
10
5
y
2
0
(x, y)
4. On the same coordinate plane, graph y = 3x – 3 and y = 3x. What do you notice?
5. Solve for y:
5y = 2x – 15
Slope-Intercept Form:
3x + 6y = 14
y = mx + b
(m = slope
Standard Form: Ax + By = C
b = y-intercept)
(Intercepts are found by letting opposite letter = 0)
6. Name the slope and y-intercept of the equation:
2x + 4y = 12
7. Name the y-intercept and x-intercept of the same equation.
8. The cost of embroidered hats is $25 for a setup fee and $15 per hat with the embroidered company
logo. Write a linear equation that will give the cost for an order of any number of hats and then graph
the equation.
9. What does a vertical line equation look like?
10. What does a horizontal line equation look like?
Unit 3 – Graphs, Linear Equations, and Inequalities in Two Variables; Functions
3.4 – Rate of Change and the Slope of a Line
The slope of a line is its rate of change:
Rise
Run
=
Vertical change
Horizontal change
=∆y
∆x
= y2 – y1
x2 – x1
Examples:
1.
Find the slope between the points (4, -5) and (3, 2). What would be the slope of a line parallel to this
created line? What would be the slope of a line perpendicular to this created line?
2.
The points (5, -2) and (-5, 9) create a line segment with what slope?
3.
Find the slope of each line
shown in the graph.
(a) line m
N
(b) line n
m
(c) line p
p
8. Use the graph to draw a line with the slope through the given point:
K(3, 1)
Slope = -2
5.
1
Find the value of r so that the line through (1, 4) and (-5, r) has a slope of 3 .
9. Find the value of r so that the line passing through (-4, r) and (-8, 3) has a slope of -5.
10. Graph the line that passes through (1, - 3) and has a slope of 4.
When reading, pay close attention to example 8:
How can you tell if two lines are parallel, perpendicular, or neither?
Unit 3 – Graphs, Linear Equations, and Inequalities in Two Variables; Functions
3.5 – Slope Intercept Form
Slope-Intercept Form: y = mx + b
1. Find the slope and y-intercept of each equation:
a. y = 7x + 3
b. y = 6 – 2/3 x
c. 10x – 2y = 6
2. Determine whether the graphs of 5y = x + 10 and 5x + y = 9 are parallel, perpendicular, or neither.
3. To promote group sales for an Alaskan cruise, a travel agency reduces the regular ticket price of $4500
by $5 for each person traveling in the group. Write a linear equation that determines the per-person
cost ‘c’ of the cruise if ‘p’ people travel together.
Unit 3 – Graphs, Linear Equations, and Inequalities in Two Variables; Functions
3.6 – Point-Slope Form
Standard Form
Ax + By = C
Slope-Intercept Form
Point-Slope Form
y = mx + b
y – y1 = m (x – x1)
Writing Equations of Lines
m (slope)
b (y-intercept)
y = mx + b
OR
m (slope) and point
y – y1 = m(x – x1)
y = mx + b
1. Write an equation of a line that passes through (-6, 1) and has a slope of ½ .
2. Write an equation of a line that passes through the points (5, 3) and (4, -3).
3. Write an equation of a line that passes through the point (4, -3) and a slope of -2.
4. Write an equation of a line that has a slope of zero. Write an equation of a line with an undefined slope.
Symbols:
Unit 3 – Graphs, Linear Equations, and Inequalities in Two Variables; Functions
3.7 – Graphing Linear Inequalities
Less than
(Strict Inequality)
is less than or equal to
Greater than
(Strict Inequality)
is greater than or equal to
Is not equal to
EX:
1. Determine if the following ordered pairs are a solution to the inequality x – y ≤ 5:
A. (-2 1)
B. (9, -1)
2. Carly is going to purchase some CDs and some DVDs. If each CD costs $12 and each DVD costs
$20, write an inequality to represents the number of CDs and DVDs she can buy if she wants to spend
$60 or less.
3. Graph 3x – y ≤ 6
4. Graph y < 3x
5. Graph 4x + 2y > 6
Unit 3 – Graphs, Linear Equations, and Inequalities in Two Variables; Functions
3.8 – Functions
domain:
(first component)
range:
(second component)
relation:
function:
Examples:
1.
State the domain and range of each. Is it a function?
a.
b.
-3
2
5
7
6
-2
“mapping”
(3, 4)
(3, 8)
(-1, 9)
“coordinate points”
c.
d. y = 2x + 2
x
1
-2
0
y
2
4
-3
“table”
2.
Does y = │x│ + 1 define a function?
3.
Find the domain and range of y = x2 + 1.
“graph”
The symbol f(x) represents a function. It is read as “f of x”.
For g(x) = 3 – 2x and h(x) = x3 – 1, find:
4.
a.
5.
g(- 4)
Graph f(x) = -3x - 2
6. Graph f(x) = │x│ + 2
b.
h(2)
7. f(x) = x2 + 1
Turn to page 299 in book. Look at self check number 7.
Use the vertical line test to determine whether or not the graphs are functions.