Download Unit 2 - WordPress.com

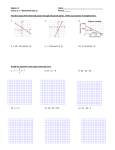
Unit 4
Section 5.8 Notes
5.8 Vocabulary
59. Negative Reciprocal – means to take a ________________ and “turn it over” and change
its sign.
Example:
60. Parallel Lines – are lines that have the same ____________ and no points of intersection.
61. Perpendicular Lines – are lines that have _________________________ slopes and
intersect at a 90º angle.
Identifying Parallel Lines - (Make sure the equations are in slope-intercept form)
Examples:
1. y = 4/3x + 3
1. Explanation
y=2
y = 4/3x – 5
y = -3
2. y = 3x + 2
y = -1/2x + 4
y = x + 2y = -4
y – 5 = 3(x – 1)
2. Explanation
Geometry Application
(4, 7)
C
(-1, 5)
A
(4, 3)
D
(-1, 1)
B
Show that the above figure is a parallelogram (a figure whose opposite sides are parallel)
Steps:
1. Find the slope of each line segment
2. Compare the slopes and determine if the opposite sides are parallel (have the same slope)
Identifying Perpendicular Lines – (make sure equations are in slope-intercept form)
Examples:
Explanation
1. x = -2
y=1
y = -4x
y + 2 = ¼(x + 1)
2. y = -4
y – 6 = 5(x + 4)
x=3
y = -1/5x + 2
Geometry Application
Q (3, 3)
(0, 1) P
(5, 0)
R
Show that PQR is a right triangle. (One pair of line segments meet at 90º)
Steps:
1. Find the slope of each line segment
2. Compare the slopes and determine if any of the segments are perpendicular(negative
reciprocal slopes)
Writing Equations of Parallel and Perpendicular Lines
Write an equation in slope-intercept form for the line that passes through (4, 5) and is parallel to
the line y = 5x + 10.
Steps
Work
1. Find the slope
1. m =
2. Plug in the slope and ordered
Pair into slope intercept equation
2. y = mx + b
3. Solve for b
3.
4. Write the equation for the parallel line
4.
Try: y = 4/5x – 6, (5, 7)
Write an equation in slope-intercept form for the line that passes through (3, 2) and is
perpendicular to the line y = 3x – 1
Steps
1. Find the slope for the perpendicular
line
Work
1. m =
2. Plug in the slope and ordered
Pair into slope-intercept equation
2. y = mx + b
3. Solve for b
3.
4. Write the equation for the perpendicular line
4.
Try: y = 5x , (-5, 3)