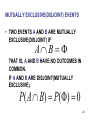Download Class Notes Number 3

CHAPTERS 5
PROBABILITY,
PROBABILITY RULES, AND
CONDITIONAL
PROBABILITY
1
PROBABILITY MODELS: FINITELY
MANY OUTCOMES
DEFINITION:
PROBABILITY IS THE STUDY OF
RANDOM OR NONDETERMINISTIC
EXPERIMENTS. IT MEASURES THE
NATURE OF UNCERTAINTY.
2
PROBABILISTIC TERMINOLOGIES
• RANDOM EXPERIMENT
AN EXPERIMENT IN WHICH ALL
OUTCOMES (RESULTS) ARE KNOWN
BUT SPECIFIC OBSERVATIONS
CANNOT BE KNOWN IN ADVANCE.
EXAMPLES:
• TOSS A COIN
• ROLL A DIE
3
SAMPLE SPACE
•
THE SET OF ALL POSSIBLE OUTCOMES OF
A RANDOM EXPERIMENT IS CALLED THE
SAMPLE SPACE.
•
NOTATION:
•
EXAMPLES
S
1. FLIP A COIN THREE TIMES
S=
4
EXAMPLE 2.
• AN EXPERIMENT CONSISTS OF FLIPPING A
COIN AND THEN FLIPPING IT A SECOND TIME
IF A HEAD OCCURS. OTHERWISE, ROLL A
DIE.
• RANDOM VARIABLE
THE OUTCOME OF AN EXPERIMENT IS
CALLED A RANDOM VARIABLE. IT CAN ALSO
BE DEFINED AS A QUANTITY THAT CAN TAKE
ON DIFFERENT VALUES.
5
EXAMPLE
• FLIP A COIN THREE TIMES. IF X
DENOTES THE OUTCOMES OF THE
THREE FLIPS, THEN X IS A RANDOM
VARIABLE AND THE SAMPLE SPACE IS
•S=
{HHH,HHT,HTH,THH,HTT,THT,TTH,TTT}
• IF Y DENOTES THE NUMBER OF HEADS
IN THREE FLIPS, THEN Y IS A RANDOM
VARIABLE. Y = {0, 1, 2, 3}
6
PROBABILITY DISTRIBUTION
•
LET X BE A RANDOM VARIABLE WITH
ASSOCIATED SAMPLE SPACE S. A
PROBABILITY DISTRIBUTION (p. d.) FOR X IS
A FUNCTION P WHOSE DOMAIN IS S, WHICH
SATISFIES THE FOLLOWING TWO
CONDITIONS:
1. 0 ≤ P (w) ≤ 1 FOR EVERY w IN S.
2.
P (S) = 1, I.E. THE SUM OF P(S) IS
ONE.
7
REMARKS
• IF P (w) IS CLOSE TO ZERO, THEN THE
OUTCOME w IS UNLIKELY TO OCCUR.
• IF P (w) IS CLOSE TO 1, THE OUTCOME
w IS VERY LIKELY TO OCCUR.
• A PROBABILITY DISTRIBUTION MUST
ASSIGN A PROBABILITY BETWEEN 0
AND 1 TO EACH OUTCOME.
• THE SUM OF THE PROBABILITY OF
ALL OUTCOMES MUST BE EXACTLY 1.
8
EXAMPLES
1. A COIN IS WEIGHTED SO THAT HEADS IS
TWICE AS LIKELY TO APPEAR AS TAILS.
FIND P(T) AND P(H).
2. THREE STUDENTS A, B AND C ARE IN A
SWIMMING RACE. A AND B HAVE THE
SAME PROBABILITY OF WINNING AND
EACH IS TWICE AS LIKELY TO WIN AS C.
FIND THE PROBABILITY THAT B OR C
WINS.
9
EVENTS
• AN EVENT IS A SUBSET OF A SAMPLE
SPACE, THAT IS, A COLLECTION OF
OUTCOMES FROM THE SAMPLE SPACE.
• EVENTS ARE DENOTED BY UPPER CASE
LETTERS, FOR EXAMPLE, A, B, C, D.
• LET E BE AN EVENT. THEN THE
PROBABILITY OF E, DENOTED P(E), IS
GIVEN BY
n
P ( E )   P ( wi )
i 1
10
FOR ANY EVENT E, 0 < P(E) < 1
• COMPUTATIONAL FORMULA
• LET E BE ANY EVENT AND S THE
SAMPLE SPACE. THE PROBABILITY OF
E, DENOTED P(E) IS COMPUTED AS
n( E )
P( E ) 
n( S )
11
EXAMPLES
1. A PAIR OF FAIR DICE IS TOSSED.
FIND THE PROBABILITY THAT THE
MAXIMUM OF THE TWO NUMBERS IS
GREATER THAN 4.
2. ONE CARD IS SELECTED AT
RANDOM FROM 50 CARDS
NUMBERED 1 TO 50. FIND THE
PROBABILITY THAT THE NUMBER
ON THE CARD IS (I) DIVISIBLE BY 5,
(II) PRIME, (III) ENDS IN THE DIGIT 2.
12
NULL EVENT: AN EVENT THAT HAS NO
CHANCE OF OCCURING. THE
PROBABILITY OF A NULL EVENT IS
ZERO.
P( NULL EVENT ) = 0
• CERTAIN OR SURE EVENT: AN
EVENT THAT IS SURE TO OCCUR.
THE PROBABILITY OF A SURE OR
CERTAIN EVENT IS ONE.
P(S) = 1
13
COMBINATION OF EVENTS
• INTERSECTION OF EVENTS
THE INTERSECTION OF TWO EVENTS A AND
B, DENOTED
A B
IS THE EVENT
CONTAINING ALL ELEMENTS(OUTCOMES)
THAT ARE COMMON TO A AND B.
14
PICTURE DEMONSTRATION
15
UNION OF EVENTS
• THE UNION OF TWO EVENTS A AND B,
DENOTED,
A B
IS THE EVENT CONTAINING ALL THE
ELEMENTS THAT BELONG TO A OR B OR
BOTH.
16
PICTURE DEMONSTRATION
17
COMPLEMENT OF AN EVENT
• THE COMPLEMENT OF AN EVENT A WITH
RESPECT TO S IS THE SUBSET OF ALL
ELEMENTS(OUTCOMES) THAT ARE NOT IN
A.
C
A
• NOTATION:
OR
'
A
P( A )  1  P( A)
C
18
PICTURE DEMONSTRATION
19
MUTUALLY EXCLUSIVE(DISJOINT) EVENTS
• TWO EVENTS A AND B ARE MUTUALLY
EXCLUSIVE(DISJOINT) IF
A B  
THAT IS, A AND B HAVE NO OUTCOMES IN
COMMON.
IF A AND B ARE DISJOINT(MUTUALLY
EXCLUSIVE),
P ( A  B )  P ( )  0
20
PICTURE DEMONSTRATION
21
ADDITION RULE
• IF A AND B ARE MUTUALLY EXCLUSIVE
EVENTS, THEN
P( A  B)  P( A)  P( B)
GENERAL ADDITION RULE
IF A AND B ARE ANY TWO EVENTS,
THEN
P( A  B)  P( A)  P( B)  P( A  B)
22
PICTURE DEMONSTRATION
23
INDEPENDENCE OF EVENTS
• TWO EVENTS A AND B ARE SAID TO BE
INDEPENDENT IF ANY OF THE FOLLOWING
EQUIVALENT CONDITIONS ARE TRUE:
P( A B)  P( A)
P( B A)  P( B)
P( A  B)  P( A).P( B)
24
CLASSWORK: EXAMPLES FROM
PRACTICE EXERCISES SHEET 2
25
CONDITIONAL PROBABILITY AND
DECISION TREES
• LET A AND B BE ANY TWO EVENTS FROM A SAMPLE
SPACE S FOR WHICH P(B) > 0. THE CONDITIONAL
PROBABILITY OF A GIVEN B, DENOTED
P( A B)
IS GIVEN BY
P( A  B)
P( A B) 
P( B)
26
CLASSWORK: EXAMPLES FROM
PRACTICE EXERCISES SHEET 2
27
GENERAL MULTIPLICATION RULE
• THE FORMULA FOR CONDITIONAL PROBABILITY
CAN BE MANIPULATED ALGEBRAICALLY SO THAT
THE JOINT PROBABILITY P(A and B) CAN BE
DETERMINED FROM THE CONDITIONAL
PROBABILITY OF AN EVENT. USING
P( A and B)
P( A B) 
P( B)
AND SOLVING FOR P(A and B), WE OBTAIN THE
GENERAL MULTIPLICATION RULE
P( A and B)  P( A B).P(B)
28
CLASSWORK: EXAMPLES FROM
PRACTICE EXERCISES SHEET 2
29
CONDITIONAL PROBABILITY
CONT’D
• CONDITIONAL PROBABLITY
THROUGH BAYE’S FORMULA
• SHALL BE SKIPPED FOR THIS
CLASS
30
BAYES’ FORMULA FOR TWO EVENTS A AND
B
• BY THE DEFINITION OF CONDITIONAL PROBABILITY,
P( A and B) P( A B).P( B)
P( B A) 

P( A)
P( A)

P( A B).P( B)
P( A B).P( B)  P( A B ).P( B )
C
C
31
CLASSWORK: EXAMPLES FROM
PRACTICE EXERCISES SHEET 2
32