Download Triangle Congruence - Hyp-Leg

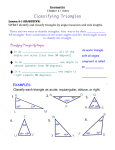
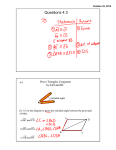
Aim: How to prove triangles are congruent
using a 5th shortcut: Hyp-Leg.
Do Now:
In a right triangle, the length of the
hypotenuse is 20 and the length of one leg
is 16. Find the length of the other leg.
12x a
c
20
b
16
Pythagorean
Theorem
a2 + b2 = c2
x2 + 162 = 202
x2 + 256 = 400
x2 = 144
x 2  144
x = 12
Aim: Triangle Congruence – Hyp-Leg
Course: Applied Geometry
Hypotenuse-Leg
HYP-LEG
V.
DABC and DA’B’C’ are
triangles
right
A’
A
B
C
B’
C’
If hypotenuse AC  hypotenuse A’C’,
and leg BC  leg B’C’
then right DABC  right DA’B’C’
If the Hyp-Leg  Hyp-Leg,
then the right triangles are congruent
Aim: Triangle Congruence – Hyp-Leg
Course: Applied Geometry
Model Problem
B
DABC, BD  AC, AB  CB.
Explain why DADB  DCDB.
A
D
C
DABC and DCBD are right triangles –
BD  AC and form right angles,
Triangles with right angles are right triangles.
AB  BC – We are told so, and both AB & BC
are hypotenuses (of DABD & DBDC respectively)
Hyp  Hyp
BD  BD – Anything is equal to itself; BD is a leg
for both right triangles - Reflexive
Leg  Leg
DADB  DCDB because of
Hyp - Leg  Hyp - Leg
Aim: Triangle Congruence – Hyp-Leg
Course: Applied Geometry
Model Problem
ABD is right, CDB is right,
AD  CB. Explain why
DADB  DCDB.
C
B
A
D
DABD and DCBD are right triangles – Triangles
with right angles are right triangles.
AD  CB – We are told so, and both AC & BD
are hypotenuses (of DBCA & DCBD respectively)
Hyp  Hyp
BD  BD – Anything is equal to itself; BD is a leg
for both right triangles - Reflexive
Leg  Leg
DADB  DCDB because of
Hyp - Leg  Hyp -Course:
Leg
Applied Geometry
Aim: Triangle Congruence – Hyp-Leg
Model Problem
PB  AC, PD  AE,
AB  AD.
Explain why DABP
 DADP
C
B
A
P
Q
D
E
DADP and DABP are right triangles –
PB
 AC and PD  AE and form right angles,
Triangles with right angles are right triangles.
AB  AD – We are told so, and each is a leg of
their respective triangles.
Leg  Leg
AP  AP – Anything is equal to itself –
Reflexive; AP is the hypotenuse of Hyp  Hyp
both
triangles
Applied Geometry
DABP  DADP H-LCourse:
 H-L
Aim: Triangle Congruence – Hyp-Leg
Model Problem
If AB  BC, DC  BC
and AC  BD, prove
DBCA  DCBD.
A
D
E
B
C
DABC and DCBD are right triangles –
AB
 BC and DC  BC and form right angles,
Triangles with right angles are right triangles.
AC  BD – We are told so, and both AC & BD
are hypotenuses (of DBCA & DCBD respectively)
Hyp  Hyp
BC  BC – Anything is equal to itself; BC is a leg
for both right triangles - Reflexive
Leg  Leg
DBCA  DCBD because of
Hyp - Leg  Hyp -Course:
Leg
Aim: Triangle Congruence – Hyp-Leg
Applied Geometry