* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Radian and Degree Measure notes
Pythagorean theorem wikipedia , lookup
Rotation matrix wikipedia , lookup
Plane of rotation wikipedia , lookup
Integer triangle wikipedia , lookup
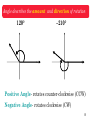
Rotation formalisms in three dimensions wikipedia , lookup
Multilateration wikipedia , lookup
Rational trigonometry wikipedia , lookup
Perceived visual angle wikipedia , lookup
History of trigonometry wikipedia , lookup
Area of a circle wikipedia , lookup
Euclidean geometry wikipedia , lookup
4.1 Radian and Degree Measure Objectives: 1.Describe angles 2.Use radian measure 3.Use degree measure 4.Use angles to model and solve real-life problems 2 Angles 3 Angles As derived from the Greek language, the word trigonometry means “measurement of triangles.” Initially, trigonometry dealt with relationships among the sides and angles of triangles. An angle is determined by rotating a ray (half-line) about its endpoint. 4 Angles The starting position of the ray is the initial side of the angle, and the position after rotation is the terminal side, as shown. Angle 5 Angles The endpoint of the ray is the vertex of the angle. Angle This perception of an angle fits a coordinate system in which the origin is the vertex and the initial side coincides with the positive x-axis. Such an angle is in standard position, as shown. Angle in standard position 6 Angles Counterclockwise rotation generates positive angles and clockwise rotation generates negative angles. Angles are labeled with Greek letters such as (alpha), (beta),an (theta), as well as uppercase letters A, B, and C. Note that angles and have the same initial and terminal sides. Such angles are coterminal. Coterminal angles 7 Angle describes the amount and direction of rotation 120° –210° Positive Angle- rotates counter-clockwise (CCW) Negative Angle- rotates clockwise (CW) 8 Angles - Review Angle = determined by rotating a ray (half-line) about its endpoint. Initial Side = the starting point of the ray Terminal Side = the position after rotation Vertex = the endpoint of the ray Positive Angles = generated by counterclockwise rotation Negative Angles = generated by clockwise rotation Angle Angle in standard position 9 Radian Measure 10 Radian Measure Measure of an Angle = determined by the amount of rotation from the initial side to the terminal side (one way to measure angle is in radians) Central Angles = an angle whose vertex is the center of the circle Central Angle 11 Radian Measure You determine the measure of an angle by the amount of rotation from the initial side to the terminal side. One way to measure angles is in radians. This type of measure is especially useful in calculus. To define a radian, you can use a central angle of a circle, one whose vertex is the center of the circle, as shown. Arc length = radius when = 1 radian 12 Radian Measure Given a circle of radius (r) with the vertex of an angle as the center of the circle, if the arc length (s) formed by intercepting the circle with the sides of the angle is the same length as the radius (r), the angle measures one radian. s r r radius of circle is r arc length is also r (s=r) initial side This angle measures 1 radian 13 Radian Measure • The radian measure of a central angle θ is obtained by dividing the arc length s by r (θ = s/r). • Because the circumference of a circle is 2 r units, it follows that a central angle of one full revolution (counterclockwise) corresponds to an arc length of s = 2 r. • Therefore, a full circle measures 2𝜋𝑟 𝑟 , or 2𝜋 radians. 14 Radian Measure Moreover, because 2 6.28, there are just over six radius lengths in a full circle, as shown. Because the units of measure for s and r are the same, the ratio s/r has no units—it is a real number. 15 Radian Measure Because the measure of an angle of one full revolution is s/r =2 r = 2 radians, you can obtain the following. r 180 ̊ 90 ̊ 60 ̊ 16 Radian Measure These and other common angles are shown below. 30 ̊ 45 ̊ 60 ̊ 90 ̊ 180 ̊ 360 ̊ 17 Radian Measure We know that the four quadrants in a coordinate system are numbered I, II, III, and IV. The figure to the right shows which angles between 0 and 2 lie in each of the four quadrants. Note that angles between 0 and are acute angles and 2 angles between and are 2 obtuse angles. 18 Comments on Radian Measure • A radian is an amount of rotation that is independent of the radius chosen for rotation • For example, all of these give a rotation of 1 radian: 1. radius of 2 rotated along an arc length of 2 2. radius of 1 rotated along an arc length of 1 3. radius of 5 rotated along an arc length of 5, etc. r1 r1 r2 1 rad r2 19 Coterminal Angles • Two angles are coterminal if they have the same initial and terminal sides. • The angles 0 and 2𝜋 are coterminal. • You can find an angle that is coterminal to a given angle θ by adding or subtracting 2𝜋. • For negative angles subtract 2𝜋 and for positive angles add 2𝜋. 20 Coterminal Angles Two angles are coterminal when they have the same initial and terminal sides. For instance, the angles 0 and 2 are coterminal, as are the angles and 13 . 6 6 You can find an angle that is coterminal to a given angle by adding or subtracting 2 (one revolution), as demonstrated in Example 1. A given angle has infinitely many coterminal angles. For instance, is coterminal with 6 where n is an integer. 21 Example 1 – Finding Coterminal Angles a. For the positive angle 13 6 coterminal angle , subtract 2 to obtain a 22 Example 1 – Finding Coterminal Angles cont’d 2 b. For the negative angle 3 coterminal angle , add 2 to obtain a 23 Example 2 – Finding Coterminal Angles Find a positive coterminal angle to 20º 20 360 380 Find a negative coterminal angle to 20º 20 360 340 15 Find 2 coterminal angles to (one positive and one negative). 4 23 15 8 15 2 4 4 4 4 15 15 8 7 8 2 4 4 4 4 4 4 24 Your Turn: Find two Coterminal Angles (+ and -) 13 6 3 4 2 3 positive negative 25𝜋 6 11𝜋 4 11𝜋 − 6 5𝜋 − 4 4𝜋 3 8𝜋 − 3 25 Complementary & Supplementary Angles Two positive angles and are complementary (complements of each other) when their sum is . 2 Two positive angles are supplementary (supplements of each other) when their sum is . Complementary angles Supplementary angles 26 Example: Complementary Angles: Two angles whose sum is 90 or (𝜋/2) radians. 6 3 2 2 6 6 6 6 3 Supplementary Angles: Two angles whose sum is 180 or 𝜋 radians. 2 3 3 2 2 3 3 3 3 27 Your Turn: Two positive angles are complementary if their sum is 𝜋/2. Two positive angles are supplementary if their sum is 𝜋. Find the Complement and Supplement 2 5 4 5 𝜋 Complement 10 3𝜋 Supplement 5 Complement - None 𝜋 Supplement 5 28 Degree Measure A second way to measure angles is in degrees, denoted by the symbol . A measure of one degree is equivalent to a rotation of of a complete revolution about the vertex. To measure angles, it is convenient to mark degrees on the circumference of a circle. 29 Degree Measure So, a full revolution (counterclockwise) corresponds to 360 deg, a half revolution to 180deg, a quarter revolution to 90deg, and so on. Because 2 radians corresponds to one complete revolution, degrees and radians are related by the equations 360 = 2 rad and 180 = rad. 2 From the latter equation, you obtain and which lead to the conversion rules in the next slide. 30 Degree Measure 31 Degree Measure When no units of angle measure are specified, radian measure is implied. For instance, = 2, implies that = 2 radians. 32 Example – Converting from Degrees to Radians a. Multiply by rad / 180. b. Multiply by rad / 180. 33 Example – Converting from Radians to Degrees 8 8 180 a. 3 3 5 5 180 b. 6 6 480 150 Multiply by 180/ rad. Multiply by 180/ rad. 34 Your Turn: Convert from degrees to radians 135° 3𝜋 4 540° 3𝜋 -270° 3𝜋 2 Convert from radians to degrees 2 rad 9 rad 2 2rad −90° 810° 360° ≈ 114.59° 𝜋 35 Equivalent Angles in Degrees and Radians Degrees Radians Degrees Radians Exact Approximate 0 0 0 90 2 1.57 30 6 .52 180 3.14 45 4 3 .79 270 3 2 4.71 1.05 360 2 6.28 60 Exact Approximate 36 Equivalent Angles in Degrees and Radians cont. 37 A Sense of Angle Sizes 45 4 30 6 90 2 See if you can guess the size of these angles first in degrees and then in radians. 2 120 3 5 150 6 60 3 180 3 135 4 You will be working so much with these angles, you should know them in both degrees and radians. 38 Applications 39 Vocabulary ►Arc ►Sector ►Tangent ►Secant ►Chord ►Segment 40 Arc, Sector, Segment ►Arc: any unbroken part of the circumference Measured in radians ►Sector: a plane figure bounded by two radii and the included arc ►Segment: a part cut off from a circle by a line, as a part of a circular area contained by an arc and its chord 41 Intercepted Arcs ►An intercepted arc is the arc that is formed when segments intersect portions of a circle and create arcs. These segments in effect 'intercept' parts of the circle. 42 Major Arcs/Minor Arcs ►The bigger one is major (≥π). The smaller is minor(<π). ►Arc HN is the minor arc ►Arc HKN is the major arc 43 Arc Lengths and Central Angles of a Circle • Given a circle of radius “r”, any angle with vertex at the center of the circle is called a “central angle”. • The portion of the circle intercepted by the central angle is called an “arc” and has a specific length called “arc length” represented by “s”. • From geometry it is know that in a specific circle the length of an arc is proportional to the measure of its central angle. • For any two central angles, 1 and 2 , with corresponding arc lengths s1 and s2 : s s2 1 1 2 44 Development of Formula for Arc Length Since this relationship is true for any two central angles and corresponding arc lengths in a circle of radius r: s1 1 s2 2 Let one angle be rad with corresponding arc length and let the other central angle be 2 rad , a whole rotation, with arc length 2r . s 2r rad 2 rad s r s s r in radians! 45 Applications The radian measure formula, measure arc length along a circle. S r can be used to 46 Example – Finding Arc Length A circle has a radius of 4 inches. Find the length of the arc intercepted by a central angle of 240deg. 47 Example – Solution To use the formula measure. S r , first convert 240deg to radian 48 Example – Solution cont’d Then, using a radius of r = 4 inches, you can find the arc length to be S r . 49 Your Turn: Finding Arc Length A circle has radius 18.2 cm. Find the length of the arc intercepted by a central angle having the following measure: 3 8 s r 3 s 18.2 cm 8 54.6 s cm 21.4cm 8 50 Your Turn: Finding Arc Length For the same circle with r = 18.2 cm and find the arc length convert 144 to radians 144 144 180 4 radians 5 cont’d = 144deg , s r 4 s 18.2 cm 5 72.8 s cm 45.7cm 5 51 Your Turn: s = rθ (s = arc length, r = radius, θ= central angle measure in radians) a. A circle has a radius of 4 inches. Find the length of the arc intercepted by a central angle of 240°. 16/3𝜋 ≈ 16.8 in b. A circle has a radius of 8 cm. Find the length of the arc intercepted by a central angle of 45° 2𝜋 ≈ 6.3 cm 52 Applications A sector of a circle is the region bounded by two radii of the circle and their intercepted arc. 53 Applications 54 Example: Find the area of the sector of a circle of radius 3 meters formed by an angle of 45 ̊. Round your answer to two decimal places. WARNING! The angle again must be given in radians Answer: 𝜋 𝜃 = 45° = 4 1 2 𝐴= 𝑟 𝜃 2 1 2 𝐴= 3 2 𝜋 4 r=3m 9𝜋 𝐴= = 3.53 𝑚2 8 55 Your Turn: Given an arc of length 4 ft and a circle of radius 7 ft, find the exact radian measure of the central angle subtended by the arc; then find the area of the sector determined by the central angle. Answer: 𝑠 4 𝑠 = 𝑟𝜃 or 𝜃 = , 𝜃 = 𝑟 7 1 2 1 2 𝐴= 𝑟 𝜃= 7 2 2 4 = 14 𝑓𝑡 2 7 56 Applications The formula for the length of a circular arc can help you analyze the motion of a particle moving at a constant speed along a circular path. 57 Linear and Angular Speed Linear speed measures how fast the particle moves, and angular speed measures how fast the angle changes. r = radius, s = length of the arc traveled, t = time, θ = angle (in radians) arc length s r Linear Speed time t t (distance/time) Ex. 55 mph, 6 ft/sec, 27 cm/min, 4.5 m/sec central angle Angular Speed time t (turn/time) Ex. 6 rev/min, 360°/day, 2π rad/hour 58 Example A bicycle wheel with a radius of 12 inches is rotating at a constant rate of 3 revolutions every 4 seconds. a) What is the linear speed of a point on the rim of this wheel? 12(6 ) 18 in / sec r t 4 56.5 in / sec 59 Example A bicycle wheel with a radius of 12 inches is rotating at a constant rate of 3 revolutions every 4 seconds. b) What is the angular speed of a point on the rim of this wheel? 6 3 radians / sec 2 4 t 60 Your Turn In 17.5 seconds, a car covers an arc intercepted by a central angle of 120˚ on a circular track with a radius of 300 meters. a) Find the car’s linear speed in m/sec. b) Find the car’s angular speed in radians/sec. 61 Picture it… 300 m 62 Solution r (a) Linear speed: t Note: θ must be expressed in radians 2 120 180 3 2 300m 3 35.9 m / sec 17.5 sec 63 Solution (b) Angular speed: t 2 3 17.5 sec ω ≈ 0.12 radians/sec 64 Example A race car engine can turn at a maximum rate of 12 000 rpm. (revolutions per minute). a)What is the angular velocity in radians per second. Solution a) Convert rpm to radians per second rev. 12 000 min 2 rad = 1256 radians/s rev sec 60 min 65 Your Turn: The second hand of a clock is 8.4 centimeters long. Find the linear speed of the tip of this second hand as it passes around the clock face. 𝑟𝜃 8.4𝑐𝑚 2𝜋 = = 16.8 𝑐𝑚 𝑚𝑖𝑛 𝑡 1𝑚𝑖𝑛 A lawn roller with a 12-inch radius makes 1.6 revolutions per second. Find the angular speed of the roller in radians per second. Find the speed of the tractor that is pulling the roller. 1.6 𝑟𝑒𝑣 2𝜋 𝑟𝑎𝑑 = = 3.2𝜋 𝑟𝑎𝑑 𝑠𝑒𝑐 𝑠𝑒𝑐 𝑟𝑒𝑣 𝑟𝜃 (12 𝑖𝑛)(3.2𝜋 𝑟𝑎𝑑) = = 38.4𝜋 𝑖𝑛 𝑠𝑒𝑐 = 6.85 𝑚𝑖 ℎ𝑟 𝑡 1 𝑠𝑒𝑐 66 Assignment 67