Download Recall from yesterday the two conjectures that you derived about the

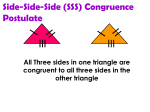
Geometry
Holt 4.4
Page 242
Notes 2.10B
Recall from yesterday the two conjectures that you derived about the SSS triangle congruence shortcut
and the SAS triangle congruence shortcut.
SSS Conjecture:
SAS Conjecture:
Example:
1. Use SSS to explain why  PQR   PSR
***Remember: The Reflexive Property of Congruence was covered in Chapter 2 page 106.
An included angle is________________________________________________________.
In order for the SAS Conjecture to be valid, the angle chosen MUST be the one included between the two
chosen sides! Not just any old angle will work!
Examples:
2. The diagram shows part of the support structure for a tower.
Use SAS to explain why  XYZ   VWZ.
***Remember: Vertical Angles are congruent was covered in Chp. 1& 2 pages 30 and 120.
3. Show that the triangles are congruent for the given value of the variable.
 UVW   YXW, x = 3
Page 244
Example 3A
You try….
Page 244
Example 3B
4.  DEF   JGH, y = 7
5.  STU   VWX, when y = 4
UT = y + 3
m  T = 20 y + 12
ST = 2y + 3
UT = 4 + 3
m  T = 20(4) + 12
ST = 2(4) + 3
UT = 7
m  T = 80 + 12
ST = 8 + 3
m  T = 920
ST = 11
T  W
ST  VW
UT  WX
So STU  VWX by SAS
6.
** Page 244
Statements
Reasons
1.
1.
2.
2.
3.
3.
4.
4.
5.
5.