Download Probability distributions

Probability distributions
Example
 Variable G denotes the population in which a
mouse belongs


G=1 : mouse belongs to population 1
G=2 : mouse belongs to population 1
 Probabilities for the two alternatives define a
probability distribution of G
P(G=1)=0.833
 P(G=2)=0.167
…if the sum of the probabilities is equal to 1:
P(G=1)+P(G=2)=0.833+0.167=1

Probability distribution as a function
 Probability distribution may be defined by a
set of probabilities for the alternative values
of a variable
 Or by a function which assigns the
probabilities to alternatives


This is especially useful when there are
many alternatives
The function usually has one or more
parameters, which control how the probability
is distributed to different values
Example : Binomial distribution
 x :Number of heads in 10 tosses of a coin
 Parameter N: number of tosses
 Parameter p: probability of heads in each trial
x | N,p ~ Bin(N,p)
P(x=k |N,p) ={ N!/(k!(N-k!)) } pk(1-p)N-k
Binomial distribution for the number
of heads in 10 tosses of a fair coin
0.3
P(x|N=10,p=0.5)
0.25
0.2
0.15
0.1
0.05
0
0
1
2
3
4
5
x
6
7
8
9
10
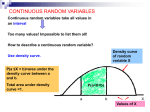
Continuous variables?
 Infinite number of possible values between any two




possible values.
->probability of any particular value = 0
There is probability density for each value: the
“height” of probability mass at that point
There is probability between two points, found by
integration
Practical calculations:


establish a dense grid of values at which to evaluate
the probability density
Normalise the density by the sum of the grid:
approximation of the amount of probability around each
grid point
Example: Normal distribution
 Possible values: all real numbers
 Parameter  : Mean of the probability mass,
center of gravity
 Parameter 2 : variance of the probability
mass, controls the spread of the probability
Probability density of x
p(x=k| , 2 )=((22) -1/2 )exp{(k- )2 / 22 }
x
340
320
300
280
260
240
220
200
180
160
140
120
100
p(x|mu=200,sigma=20)
Normal distribution
0.025
0.02
0.015
0.01
0.005
0
Describing the probability distribution






Mean
Variance
Standard deviation
Median and other percentiles
Mode
Coefficient of variation
k
340
320
300
280
260
240
220
200
180
160
140
120
100
P(x<k |mu=200,sigma=20)
Cumulative distribution
1.2
1
0.8
0.6
0.4
0.2
0
Exercise 3
 Make a graph showing the probability density
of a Normal distribution with mean = 100 and
standard deviation of 10. Evaluate the density
at values 50,55,60,65,…,150
 Using the grid approximation, calculate the
following statistics of the distribution




Mean
Variance
Standard deviation
Coefficient of variation
Exercise 3 continues
 By using the grid approximation, calculate the
cumulative distribution of the previously
defined normal distribution
 Use the graph to determine the following
statistics



Median
5% percentile
95% precentile