* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Measuring and Drawing Angles and Triangles
History of trigonometry wikipedia , lookup
Perspective (graphical) wikipedia , lookup
Multilateration wikipedia , lookup
History of geometry wikipedia , lookup
Technical drawing wikipedia , lookup
Perceived visual angle wikipedia , lookup
Integer triangle wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Euler angles wikipedia , lookup
Trigonometric functions wikipedia , lookup
Rational trigonometry wikipedia , lookup
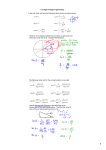
NAME DATE Measuring and Drawing Angles and Triangles Measuring an angle 30° arm origin If the arms are too short to reach the protractor scale, lengthen them. Step 1: Place the origin of the protractor over the vertex of the angle. Step 2: Rotate the protractor so the base line is exactly along one of the arms of the angle. 0° 0° 180° base line Step 3: Look at that arm of the angle and choose the scale that starts at 0°. Step 4: Use that scale to find the measurement. Drawing an angle angle mark angle mark 60° Step 1: Draw a line segment. Step 2: Place the protractor with the origin on one endpoint. This point will be the vertex of the angle. Step 3: Hold the protractor in place and mark a point at the angle measure you want. Step 4: Draw a line from the vertex through the angle mark. Drawing lines that intersect at an angle 45° P Step 1: Draw a line. Mark a point P on the line. 45° P Step 2: Draw an angle of the given measure using P as vertex. P Step 3: Extend the arms of your angle to form lines. 90° 30° 5 cm 90° 5 cm 5 cm Step 1: Sketch the Step 2: Use a ruler to draw triangle you want to draw. one side of the triangle. E-42 90° 30° 5 cm Step 3: Use a protractor to draw the angles at each end of this side. Extend the arms until they intersect. 90° 30° 5 cm Step 2: Erase any extra arm lengths. Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 COPYRIGHT © 2010 JUMP MATH: TO BE COPIED Drawing a triangle NAME DATE Drawing Perpendicular Lines and Bisectors Drawing a line segment perpendicular to AB through point P Using a set square P A P B A P B P A A B Here point P is on AB. B Here point P is outside AB. Using a protractor P A B P A P B P B A Here point P is on AB. A B Here point P is outside AB. Drawing the perpendicular bisector of line segment AB A M A B COPYRIGHT © 2010 JUMP MATH: TO BE COPIED A Step 1: Use a ruler to determine the midpoint of the line segment. Label it M. M M B A M B B Step 2: Use a set square or a protractor to draw a line perpendicular to AB that passes through M. Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 The line you have drawn is the perpendicular bisector of AB. E-43 NAME DATE Drawing Parallel Lines Drawing a line parallel to AB through point P Using a set square P A P P A B Step 1: Line up one of the short sides of the set square with AB. P A B A Step 2: Use the set square and a straight-edge to draw a perpendicular to AB. B B Step 3: Draw a line perpendicular to the new line that passes through P. Step 4: Erase the line you no longer need. Using a protractor P A P P B A B B A B Step 2: Line up the 90° line on the protractor with the line segment drawn in step 1, and the straight side of the protractor with point P. Draw a line parallel to AB. Erase the first perpendicular you drew. COPYRIGHT © 2010 JUMP MATH: TO BE COPIED Step 1: Line up the 90° line on the protractor with AB. Use the straight side of the protractor to draw a line segment perpendicular to AB. A P E-44 Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 NAME DATE Properties of Parallel Lines Investigation What happens if two lines meet a third line at the same angle, but it is not a right angle? A. Draw a pair of parallel lines and a third line intersecting both at an angle that is not a right angle. B. ∠ABD = ∠ACE = 70°. Draw a perpendicular to BD through point A. Extend it to meet CE. Is the line you drew perpendicular to CE? Check using a protractor. What can you say about the lines BD and CE? E D C B A D C. ∠ABD = ∠ACE = 70°. Are the lines BD and CE parallel? E B A C D. Draw a pair of lines that intersect at a 40° angle. Draw a third line that meets one of the lines at the same angle. Try to make the third line parallel to one of the lines you started with. Check by drawing a perpendicular. E. Compare the pattern between the equal angles ∠ABD and ∠ACE in parts B and D. Which one looks more like the angles marked in the letter C and which one is more like angles in the letter F? COPYRIGHT © 2010 JUMP MATH: TO BE COPIED Mathematicians have proved that if two lines meet with a third line at the same angles creating a pattern like in the letter F, the lines are parallel. When the lines meet at a right angle, you do not have to worry about the pattern of equal angles—they are all right angles. Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 C E B D A C E A B D E-45 NAME DATE Distance Between Parallel Lines InveStIgatIon Does the distance between parallel lines depend on where you measure it? a. Measure the line segments with endpoints on the two parallel lines with a ruler. Write the lengths of the line segments on the picture. B. Use a square corner to draw at least three perpendiculars from one parallel line to the other, as shown. Measure the distance between the two parallel lines along the perpendiculars. What do you notice? C. Explain why all the perpendiculars you drew in part B are parallel. e. Measure the line segments you drew between the two given parallel lines in part D. What do you notice? F. To measure the distance between two parallel lines, draw a line segment perpendicular to both lines and measure it. Does the distance between parallel lines depend on where you measure it? E-46 Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 COPYRIGHT © 2010 JUMP MATH: TO BE COPIED D. A parallelogram is a 4-sided polygon with opposite sides parallel. You can draw parallelograms by using anything with parallel sides, like a ruler. Place a ruler across both of the parallel lines and draw a line segment along each side of the ruler. Use this method to draw at least 3 parallelograms with different angles. NAME DATE Sum of the Angles in a Triangle Investigation What is the sum of the angles in a triangle? A. Circle the combinations of a 70° angle and another angle that will make a triangle. (Hint: Imagine the sides of the triangle extended—will they ever intersect?) 70° 80° 70° 90° 70° 100° 70° 110° 70° 120° Circle the combinations of a 50° angle and another angle that will make a triangle. 50° 100° 50° 110° 50° 120° 50° 130° 50° 140° Circle the combinations of a 90° angle and another angle that will make a triangle. 90° 70° 90° 80° 90° 90° 90° 100° 90° Make a prediction: To make a triangle, the total measures of any two angles must be less than °. 110° B. List the sum of the measures of the angles in each triangle. 90° ° + ° + ° = ° COPYRIGHT © 2010 JUMP MATH: TO BE COPIED 118° 55° 68° 42° 57° 20° 70° ° + ° + ° = ° 25° 20° 25° 130° ° + ° + ° = ° ° + ° + ° = ° What do you notice about the sums of the angles? Do you think this result will be true for all triangles? Make a conjecture: The sum of the three angles in any triangle will always be °. Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 E-47 NAME DATE C. Calculate the sum of the angles. 70° °+ 90° °+ 42° 57° 20° °= ° °+ 68° 55° °+ °= 25° 25° 118° ° 130° 20° °+ °+ °= ° °+ °+ °= ° What do you notice about the sums of the angles? D. Cut out a paper triangle and fold it as follows: C A B Step 1: Find the midpoints of the sides adjacent to the largest angle (measure or fold). Draw a line between the midpoints. A B C Step 2: Fold the triangle along the new line so that the top vertex meets the base of the triangle. You will get a trapezoid. A C B Step 3: Fold the other two vertices of the triangle so that they meet the top vertex. The three vertices folded together add up to a straight angle. What is the sum of the angles in a straight angle? ° e. Could you fold the vertices of any triangle along a line and get a straight angle as you did in part D? Do the results of the paper folding activity support your conjecture in part B? Explain. F. In fact, it has been mathematically proven that… the sum of the angles in a triangle is E-48 °. Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 COPYRIGHT © 2010 JUMP MATH: TO BE COPIED So ∠A + ∠B + ∠C = ° NAME DATE Straw Quadrilaterals 1. Take 6 straws. • Leave 2 straws whole. • Cut 2 straws in half. • Cut 2 straws into a quarter straw and a three-quarter straw. 2. Make as many quadrilaterals as you can with the combinations of 4 straws below. • Try placing the straws at different angles. • Try placing the straws in different orders. Sketch the quadrilaterals you make. a) 2 whole straws and 2 quarter straws b) 4 half straws c) 1 whole straw, 1 three-quarter straw, and 2 half straws d) 1 whole straw, 1 three-quarter straw, 1 half straw, and 1 quarter straw 3. Check off the correct ending for the statement. COPYRIGHT © 2010 JUMP MATH: TO BE COPIED With any of the four given side lengths above, only one possible quadrilateral can be made exactly two different quadrilaterals can be made many different quadrilaterals can be made Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 E-49 NAME DATE COPYRIGHT © 2010 JUMP MATH: TO BE COPIED Protractors E-50 Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 NAME DATE COPYRIGHT © 2010 JUMP MATH: TO BE COPIED Circles Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 E-51 NAME DATE Quadrilaterals (1) 2 3 4 5 6 COPYRIGHT © 2010 JUMP MATH: TO BE COPIED 1 E-52 Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 NAME DATE Quadrilaterals (2) 8 9 10 11 12 COPYRIGHT © 2010 JUMP MATH: TO BE COPIED 7 Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 E-53 NAME DATE 2-D Shapes Sorting Game (1) 13 14 More than one line of symmetry 15 No lines of symmetry No right angles Two or more right angles 17 Two or more acute angles E-54 16 18 Equilateral Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 COPYRIGHT © 2010 JUMP MATH: TO BE COPIED NAME DATE 2-D Shapes Sorting Game (2) 19 20 Not equilateral No obtuse angles 21 One or more acute angles COPYRIGHT © 2010 JUMP MATH: TO BE COPIED 23 At least two pairs of parallel sides 22 At least one reflexive angle 24 All angles equal Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1 E-55 NAME DATE COPYRIGHT © 2010 JUMP MATH: TO BE COPIED Regular Polygons E-56 Blackline Master — Geometry — Teacher’s Guide for Workbook 7.1