* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Population Genetics Notes
Source–sink dynamics wikipedia , lookup
Two-child policy wikipedia , lookup
The Population Bomb wikipedia , lookup
Human overpopulation wikipedia , lookup
Storage effect wikipedia , lookup
World population wikipedia , lookup
Human population planning wikipedia , lookup
Maximum sustainable yield wikipedia , lookup
Population Studies
Introduction of Some terms
A population
consists of all the members of a species that
occupy a particular area at the same time
The members of a population are more likely
to breed with one another than with other
populations of the same species
Therefore, genes tend to stay in the same
population for generation after generation
INTRODUCTION
The total of all the genes in all the members of a
population at one time is called the …
population's gene pool
Evolution
is the change in the frequency of genes…
in a population's gene pool…
from one generation to the next.
Hardy-Weinberg Law
In order to see how a population evolves, it is
helpful to examine the genetics of a
population that does not change from
generation to generation
The Hardy-Weinberg Law provides a model
of an unchanging gene pool
This law states that the frequencies of alleles
in a population's gene pool remain constant
over generations if all other factors remain
constant
Hardy-Weinberg Law
For a gene pool to be in the Hardy-Weinberg
equilibrium, 5 conditions must be met:
1. The population must be closed. This means that no
2.
3.
4.
5.
immigration or emigration can occur.
Random mating takes place. There can be no mating
preferences with respect to genotype.
There can be no selection pressure. A specific gene
must not affect the survival of the offspring.
No mutation of the particular alleles examined can
occur.
The population must be very large. This equilibrium is
based on statistical probabilities and random sampling.
Hardy-Weinberg Law
If all these conditions are met, the
frequencies of two alleles (A and a) will
remain constant in a population forever
or until conditions change
Recall our definition of Evolution
Change of frequency of genes or alleles
The Hardy-Weinberg law points out that
sexual reproduction reshuffles genes but does
not by itself cause evolution
Hardy-Weinberg Law
The mathematical expression of the Hardy-
Weinberg equilibrium is…
p+q=1
where p = frequency of the dominant allele
&
q = frequency of the recessive allele
Hardy-Weinberg Law
Example:
suppose a certain allele A has a frequency of 0.6 in
a population
since the two alleles must add up to 1… then
p + q = 1 (1 - 0.6 = 0.4)
the frequency of a is 0.4
Let's see what happens during reproduction
Hardy-Weinberg Law
First, let’s arrange the two alleles and their
frequencies on a Punnett square
A
(0.6)
A
(0.6)
a
(0.4)
a
(0.4)
Hardy-Weinberg Law
Then, fill in frequencies for the possible
offspring
A
(0.6)
a
(0.4)
A
(0.6)
a
(0.4)
AA
(0.36)
Aa
(0.24)
Aa
(0.24)
aa
(0.16)
Hardy-Weinberg Law
Go ahead and add up your values for the allele
frequencies.
What do you get?
The mathematical relationship governing the gene
frequencies is…
p2 + 2pq + q2 = 1
AA + 2Aa + aa = 1 (or 100%)
Since p = 0.6 and q = 0.4, then
(0.6)2 + 2 (0.4 x 0.6) + (0.4)2 must equal 1
(0.36) + 2(0.24) + (0.16) = 1
Practice
Mutations & Evolutionary Change
Mutations violate the conditions for Hardy-
Weinberg equilibrium because one gene
changes into another and therefore alters
gene frequencies in the population
Mutations & Evolutionary Change
Review: a mutation is any inheritable change in the
DNA of an organism
1. Chromosome mutation
results form non-disjunction, chromosome breakage
or translocation
2. Gene mutation
changes in the nucleotides of a DNA molecule
If a population has a stable gene pool and
gene frequencies, it is not evolving.
Mutations
If the population does not demonstrate
Hardy-Weinberg equilibrium (i.e. its gene
frequencies are not stable) it is in
evolutionary change
Evolutionary Change
Micro-evolution
a change in the gene pool of a population over
successive generations
Potential causes of micro-evolution are
mutation
genetic drift
gene flow
non-random mating
natural selection
Evolutionary Change
Mutation
A new mutation that is transmitted in gametes
immediately changes the gene pool of a
population by substituting one allele for another
A mutation by itself does not have much effect on
a large population in a single generation
If, however, the mutation gives selective
advantage to individuals carrying it, then it will
increase in frequency and the population gene
pool will change over successive generations
Evolutionary Change
Genetic drift
evolution can occur simply by chance
Random events may bring death or parenthood to
some individuals regardless of their genetic
makeup
The resulting change in the gene pool is called
genetic drift
Genetic drift plays more of a role in small
populations than in large ones
Evolutionary Change
Genetic drift
Example
Flipping a coin 1000 times compared with flipping a
coin 10 times
Example
a population of plants consists of only 25 individuals,
16 are AA, 8 are Aa and 1 is aa
AA plants are destroyed in a rock slide, which alters
the relative gene frequencies for subsequent
populations.
Evolutionary Change
Founder Effect
Genetic drift that occurs when a small number of
individuals separate form their original population and
start a new population
Allele frequencies of the new population will be different
than the original population
o depend on gene pool of the founding population
Evolutionary Change
Bottleneck Effect
A dramatic reduction in population size resulting in
genetic drift
The frequency of alleles in the remaining members of the
population is very different from the original population.
Evolutionary Change
Gene flow
The gene pools of most populations of the same
species exchange genes.
This violates the Hardy-Weinberg condition that
populations must be closed to be in equilibrium
Animals may leave one area and contribute their
genes to the pool of a neighbouring population
migration
or a high wind may disperse seeds or pollen far
beyond the bounds of the local population
Gene flow between populations may change gene
frequencies and therefore may result in evolution
Nonrandom Mating
Mates are chosen based on different
characteristics (not just love the one you’re
with)
Sexual Selection
Chances of being selected depend on animal’s
traits (what makes him more desirable to the
female)
Includes Physical and Behavioural Differences
between sexes
Nonrandom Mating
Sexual Dimorphism
Striking physical differences between males and
females
Male
Male
Female
Female
Nonrandom Mating
Natural Selection
Environment selects for particular traits that are
more favourable for surviving in that environment
“Survival of the Fittest”
Population Interactions Definitions
Population – Any group of individuals of the same
species who live in the same area at the same time
Eg. Population of humans in the food court
Community – The association of interacting
populations that live in a defined area
Eg. Population of the food court, tables, chairs, trays, and
pets and wild animals that wander into the food court.
Niche – An organism’s habitat and role within a
community
Includes all factors needed to survive and the organism’s
interactions with other species
Population Interactions
In any community, individuals of many
populations need to live among each other
Some possible scenarios:
Competing for limited resources
One species preying on another
One species relying on another for survival
Competition occurs whenever two or more
organisms attempt to exploit a limited resource
Food
Living space
Population Dynamics
The interactions among individuals – either
within the same population or from different
populations – are the driving force behind
population dynamics
The changes that occur in a population over time
Population Dynamics
Individuals are always competing for resources
in order to survive
Competition for resources can occur:
Among individuals of the same species
Natural selection
Survival of the fittest
Between individuals of different species
Hence, there are two basic categories of
competition
Intraspecific Competition
Intraspecific competition – Competition for
limited resources among members of the same
species
SURVIVAL OF THE FITTEST among members of the
same species aka NATURAL SELECTION
Eg. Seeds
On the forest floor there are thousands of seeds
Each seed requires water, nutrients, sunlight, space to
grow and mature
Only a few seeds will be able to compete successfully to
obtain what they need of the limited available resources
Intraspecific Competition
Intra-specific competition is very
common since the members of a
population have the same
requirements
Intra-specific competition occurs
when individuals of a species are
competing for resources within their
niche
Interspecific Competition
Interspecific competition – Competition for limited
resources between members of different species
in the same community
Tree competing with a shrub for light and growing space
Recall a niche is an organism’s habitat and role in a
community
Due to interspecific competition, no two
organisms can share the exact same ecological
niche
Interspecific Competition
If no two species can share the exact
same ecological niche – then why is
there interspecific compeition?
Interspecific competition occurs when
individuals of two different species are
competing for resources within
overlapping niches
Competition – Gause’s Principle
The Theory of Competitive Exclusion
Two species with very similar niches
cannot survive together because they
compete so intensely that one species
eliminates the other
Competition – Gause’s Principle
Experiment: Gause raised two species of paramecium with
similar food requirements in the same culture
One species always eliminated the other (the particular
conditions in the culture determined which species
survived)
In nature, species can avoid direct competition by
Feeding at different times of the day (e.g. Hawks and owls)
Dividing resources in some other way (e.g. Different
organisms hunt for insects in different parts of coniferous
trees)
Producer-Consumer Interactions
Not all interspecific interactions in a
community are classified as competitive…
Predation
The most obvious population interaction in a
community are those in which a predator eats its
prey
Predators that specialize in eating only one prey
species play an important role in controlling the
population size of the prey species
Eg. Canada lynx and snowshoe hare
The terms predator and prey apply not only to
animals that eat other animals, but to any type
of producer and consumer relationship
Eg. Plants and Herbivores
Predation
Plant defense mechanisms against
herbivores:
Thorns
Microscopic crystals in their tissues
Spines or hooks on leaves
Distasteful or harmful chemicals
Some well-known poisons and drugs
are secondary compounds produced
by plants:
Strychnine
Morphine
Nicotine
Mescaline
Predation
Active animal
defenses against
predation
Fighting
Hiding
Escaping
Four types of passive
defense
Predation – Passive Defense
Type I Mechanical or chemical defense mechanisms
include porcupine quills, the skunk's offensive odour,
the bad taste of monarch butterflies
Predation – Passive Defense
Type II
Camouflage or protective coloration makes it
difficult to spot prey
Predation – Passive Defense
Type III
Deceptive coloration, warning coloration
Predation – Passive Defense
Type IV
Mimicry, where one
species resembles
another
Monarch and viceroy
butterflies
Coral snake and harmless
species
Wasps and non-biting flies
Symbiotic Relationships
Symbiosis is a close relationship between members of
different species (3 categories)
1. Mutualism - Both species benefit from the association
Coliform bacteria in the human gut, nitrogen-fixing bacteria
in nodules of legumes, protists in a termite's gut
2. Commensalism - One species benefits while the other
neither benefits nor is harmed
Remora and the shark
3. Parasitism - One species, the parasite, benefits at the
expense of the host
The parasite takes nourishment directly from the tissues of
its host's body
Marc’s Botfly
Marc’s Botfly
After Central America
Regulation of Population Size
Factors Affecting Growth of Populations
The growth of a population is suppressed by
Abiotic factors - Non living things in the environment
Sunlight, water, soil, air
Biotic factors - Living things in the environment
Humans, trees, fish, bacteria
The combination of these effects is termed
environmental resistance
Factors that regulate the growth of populations are
described as density-dependent or densityindependent
Regulation of Population Size
The combination of biotic (living) and abiotic
(nonliving) factors create environmental
resistance
Environmental resistance = the combined effects of
various interacting factors that limit population
growth
There are two categories of factors that
regulate the growth of populations
1. Density-dependent
2. Density-independent
Density Dependent Factors
These factors are intensified as the
population increases in size
Food availability
Living space
Emigration
Competition
Disease
Reproductive rate
Mortality
Accumulation of
Parasitism
wastes
Immigration
Biotic Factors
Density-Independent
The occurrence and severity of these factors
are unrelated to population size
Weather
Climate
Abiotic factors
Growth and Regulation of Populations
Population Density
Population density = The number of individual
organisms in a given area or volume
Population Density
Dp = N or
A
Dp = N
V
D = Density
N = number of organisms
A= area
V = volume
Growth and Regulation of Populations
Population Density
Example:
44 students/100m2 = 0.44 students/m2
12 gophers/10.0m2 = 1.2 gophers/m2
54 minnows/200 mL = 0.27 minnows/mL
Growth and Regulation of Populations
Population Density
Why calculate population density?
If you know your community size you can now
estimate the size of your population
Examples:
School = 1000m2, therefore
4.4 students/m2 x 1000m2 = 4400 students
Field = 200m2, therefore
1.2 gophers/m2 x 200m2 = 240 gophers
Fish tank = 2L = 2000 mL, therefore
0.27 minnows/mL x 2000mL = 540 minnows
Population Density Practice
A fish tank 10m long, 5m tall and 2m wide
is filled with water.
The population density of bacteria in the
water is 1.5 x 104bacteria/m3
Approximately how many bacteria are in
the fish tank?
Population Density Practice–cont’d
First we need to calculate the volume of the
swimming pool:
10m x 5m x 2m = 100m3
The population density of the bacteria is
1.5 x 104bacteria/m3
Therefore, the population density of bacteria
in the water is represented by the formula
Dp = N
Dp x V = N
V
Population Density Practice–cont’d
Dp x V = N
N = 1.5 x 104bacteria/m3 x 100m3
= 1 500 000
= 1.5 x 106 bacteria
Growth and Regulation of Populations
Population Density
Is this always 100% accurate?
Note that you need to know how a
population is distributed within its habitat
before taking samples to determine the
population size
Some populations tend to clump in certain
areas, which can affect the accuracy of your
estimation
Growth and Regulation of Populations
Population Growth
A population gains individuals by:
Natality = Birth
Immigration
A population loses individuals by:
Mortality = Death
Emigration
The balance between these four factors will
determine whether a population size grows,
declines, or remains the same
Growth and Regulation of Populations
Change in Population Size
Although this is the formula given to you, we know that
Factors that increase population = births and immigration
Factors that decrease population = deaths and emigration
Therefore,
(D N) = (births + immigration) - (deaths + emigration)
Growth and Regulation of Populations
Calculate the change in the Sandhill Crane
population at the banks island breeding site in
1991
Births = 40, Immigrations = 0
Deaths = 55, Emigration = 0
Initial number = 200
(D N) = (births + immigration) - (deaths + emigration)
N = (40 + 0) - (55 + 0) = - 15 individuals
Growth and Regulation of Populations
Percent Population Growth
Formula – not given on your data sheet but is intuitive…
Recall that change in population is represented by:
(D N) = (births + immigration) - (deaths + emigration)
Therefore, percent growth = Change in population x 100%
Initial population
=> Percent growth =
__[b + i] - [ d + e]_
Initial population
x 100%
Growth and Regulation of Populations
Percent Population Growth
Example:
Births = 40
Deaths = 55
Initial population size = 200
=>Percent growth = __[b + i] - [ d + e]_ x 100%
Initial population
PG% = [40 + 0] - [55 + 0] x 100% = -7.5%
200
Growth and Regulation of
Populations
Population Growth Rate
Population growth rate:
The change in the number of organisms in a
population per unit time
growth rate = _D N_
Dt
Growth and Regulation of Populations
Per Capita Growth Rate
Rate of population growth does not take into account the
initial size of the population
A large population has more individuals that can
reproduce compared to a small population
To compare populations of the same species that are
different sizes or live in different habitats, the change in
population size can be expressed as the rate of change per
individual
This measurement gives us per capita growth rate
Growth and Regulation of Populations
Per Capita Growth Rate
The per capita growth rate can be calculated by
the formula:
cgr = ΔN
N
cgr = Per capita growth rate
ΔN = Change in the number of individuals
in a population
N = The original number in the population
Growth and Regulation of Populations
Per Capita Growth Rate
Why measure per capita growth rate?
To examine population size as the rate of
change per individual
Eg. Suppose that in a town of 1000 people
there are 50 births, 30 deaths, and no
immigration or emigration in a year.
Calculate the per capita growth rate.
Growth and Regulation of Populations
Per Capita Growth Rate
Eg. Suppose that in a town of 1000 people there
are 50 births, 30 deaths, and no immigration or
emigration in a year. Calculate the per capita
growth rate.
cgr (Growth rate) = Unknown
ΔN = 50 births – 30 deaths = +20
N = 1000 people
cgr = ΔN =
N
20 = 0.02 people
1000
Could the answer be a negative value?
Factors that Affect
Population Growth
Recall that both biotic and abiotic factors
limit the growth of a population
Population size can be limited by
How fast and how often a species can reproduce
The ability of a habitat to support the population
Biotic Potential of Populations
Biotic potential = r
Definition = The maximum number of
offspring that can be produced by a
species under ideal conditions
ie. The capacity of populations for exponential
growth
There are six factors which affect biotic
potential of a population
Biotic Potential of Populations
Six Factors that affect Biotic Potential
1. Age of onset of sexual maturity
• The earlier that sexual maturation occurs, the
greater the biotic potential
2. Gender ratio
• The more females there are, the greater the
biotic potential
3. Estrous cycles
• The shorter the time between cycles of sexual
receptivity, the greater the biotic potential
Biotic Potential of Populations
Six Factors that affect Biotic Potential
4. Mate availability
The more readily available mates are in a
population, the greater the biotic potential
5. Litter or clutch size
The larger the litter or clutch size, the greater the
biotic potential
6. Fecundity
Fecundity = average number of offspring
produced per female
The greater the fecundity of a species the greater
the biotic potential
Population Growth Patterns
Two Types of Graphs/Curves to know:
1. Exponential Population Growth: J-Curve
This model predicts unlimited population increase
under ideal conditions (usually a closed pop.) of
unlimited resources and then a sharp decline in the
population
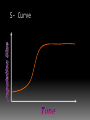
2. Logistic Growth: S-Curve
More representative of population in nature
This model incorporates the effects of resource
limitation and crowding on the population growth
rate
Population Growth Patterns
1. Exponential Population Growth: J-Curve
This model predicts unlimited population increase
under ideal conditions (usually a closed pop.) of
unlimited resources and then a sharp decline in the
population
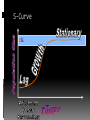
There four phases in this type of growth pattern:
1.
2.
3.
4.
Lag phase
Growth phase
Stationary phase
Death phase ("crash")
Examples of organisms that exhibit exponential
growth include bacteria, yeast, some insects
J-Curve
J-Curve
J-Curve
J-Curve
Population Growth Patterns
2. Logistic Growth: S-Curve
More representative of population in nature
This model incorporates the effects of resource
limitation and crowding on the population growth
rate
Natural populations cannot continue to grow
exponentially:
There is a limit to the number of individuals that can
occupy a habitat
The carrying capacity is the maximum stable
population size that the environment can support
for a long period of time.
S- Curve
Population Growth Patterns
Logistic Growth: S-Curve – cont’d
In populations exhibiting logistic growth,
an equilibrium is reached near the carrying
capacity of the environment
example p. 585 figure 25.12
Carrying capacity (symbolized as K) is a
property of the environment, and it varies
over space and time with the abundance
of limiting resources
S-Curve
Carrying
Capacity
S-Curve
K
R-SELECTED
AND
K-SELECTED
POPULATION STRATEGIES
r-selected Populations
Experience periods of exponential growth
Characteristics of r-selected species:
Small organisms
Short life time
Great reproductive potential
Recall biotic potential (r) is the capacity of populations to
grow exponentially
High rate of reproduction = r
Insects are examples of r-selected
populations
K-selected Populations
Populations that stabilize near the carrying
capacity of their environment (K)
Characteristics of K-selected species:
Larger size
Longer generation time
Lower reproductive potential
Examples include large mammals such as deer,
bears, and humans
A COMPARISON OF
R-SELECTED (OPPORTUNISTIC)
AND
K-SELECTED (EQUILIBRIAL)
POPULATIONS
R-Selection
K-Selection
Climate
Variable and/or
unpredictable
Fairly constant and/or
predictable
Mortality
Density independent
Density dependent
Survivorship
High juvenile mortality
Low juvenile mortality
Population Size
Variable, below carrying
capacity
Fairly constant, near carrying
capacity
Level of competition
Low
High
Life History
Rapid development
Slow development
Reproductive Capacity
High reproductive capacity
Greater competitive ability
Age Sexual Maturity
Early reproduction
Delayed reproduction
Body Size
Small body size
Large body size
Reproductive Frequency
Usually reproduce only
once
Repeated reproduction
Offspring
Many small offspring
Fewer, larger offspring
Length of Life
Short, less than one year
Longer, usually more than one
year
Change in Communities: Succession
Succession - The sequence of invasion and
replacement of species in an ecosystem over time
The sequence of
identifiable ecological
stages or communities
occurring over time in
progress from bare
rock to climax
community
Affected by abiotic
and biotic factors –
climate and
interspecific
competition
Change in Communities: Succession
Communities are defined by the populations
in them
The stage of succession can be determined
by the kinds of species present in a
community
Change in Communities: Succession
Primary succession
The initial colonization of
a barren habitat by
pioneer species
Soil is produced during
this stage
e.g. Lichen and mosses
growing on rocks
Secondary succession
Re-building of an area that
once supported many
organisms
e.g. Mount St. Helen’s
Change in Communities: Succession
Climax Community
The stage in ecological
succession that is stable and selfsupporting
Usually the final stage in the
stages of succession
Produce more organic material
than they use
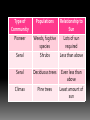
Type of
Community
Populations
Relationship to
Sun
Pioneer
Weeds, fugitive
species
Lots of sun
required
Seral
Shrubs
Less than above
Seral
Deciduous trees
Even less than
above
Climax
Pine trees
Least amount of
sun