* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download B-3DPhysicalAcoustics3
Survey
Document related concepts
Transcript
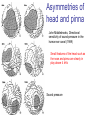
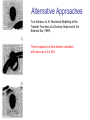
MUS_TECH 348 3-D Sound and Spatial Audio Physical Modeling Problem: Can we model the physical acoustics of the directional hearing system and thereby understand the relationship between the physical system and the HRTF? Consider the head as a Sphere Predictions of sound intensity and phase can be verified with acoustic measurements. Francis Wiener “Sound Diffraction by Rigid Sphere and Circular Cylinders (1947) Measurement are expressed relative to 1/3 < ka < 10, where a is the radius of the sphere and k is the wave number. Consider the head as a Sphere Francis Wiener “Sound Diffraction by Rigid Sphere and Circular Cylinders (1947) Comparison of predictions and measurements. Sound pressure Head as a Sphere One verified prediction is that there will be a ‘bright spot’ in the back of the sphere. ka = 0.5, 1 ka = 2, 3 ka = 4, 5 Sound pressure ka = 6,7 ka = 8, 10 Head as a Sphere Rayleigh diffraction transfer function predicts ripples in magnitude and group delay. magnitude group delay Head as a Sphere “Creeping waves” are created at shadow zone boundaries. Anthony J. Rudgers, Acoustic Pulses Scattered by a Rigid Sphere Immersed in a Fluid (1968) creeping wave Plane wave radius=a shadow zone •Speed is less than usual speed of sound, 97% for high frequencies •Amplitude decreases exponentially Changes with distance Richard Duda and William Martens, Rangedependence of the HRTF for a Spherical Head (1997) The plane wave assumption breaks down when sources are close to sphere. ILD = interaural level difference predicted on basis of sphere with ears set back 10-degrees p is normalized distance relative to sphere radius Correlation with Dummy Head George Kuhn, Model for the interaural time differences in the azimuthal plane (1977) and Towards a Model for Sound Localization (1982) Compare predictions with measures done with dummy head. •ITD below 500 Hz is independent of frequency 3 (head radius/ speed of sound) sin q •ITD above 3000 Hz is independent of frequency 2 (head radius/ speed of sound) sin q •Minimum ITD appear around 1,500 Hz •Between the low and high frequency regions there is a considerable difference between phase delay and group delay High frequency delays are 2/3 of low frequency delays. George Kuhn, Model for the interaural time differences in the azimuthal plane (1977) Phase Delay p unwrap w phase q(w) -p -2p q(w) phase delay = - w msec w Group Delay p unwrap w phase q(w) -p -2p d q(w) group delay = - d w msec w Phase Delay and Group Delay Measures phase delay and group delay differ. The more difficult question is in what way does the auditory system responds to delay. Asymmetries of head and pinna John Middlebrooks, Directional sensitivity of sound-pressure in the human ear canal (1989) Small features of the head such as the nose and pinna are clearly in play above 4 kHz Sound pressure Asymmetries of head and pinna John Middlebrooks, Directional dependence of interaural envelope delays (1990) Envelope delay is more appropriate for sound above 4 kHz due to what we know about how the auditory system detects delays. Modeling the Pinna Filter Notches in the HRTF are the result of delayed energy. Can we model the source? Comb filter + delay f Pinna filter + filter delay f Modeling the Torso Algazi, Duda and Thompson, “The use of Head- and-Torso Models for Improved Spatial Sound Synthesis (2002) This is an example of using a model to create better directional hearing cues. Modeling the Torso Algazi, Duda and Thompson, “The use of Head- and-Torso Models for Improved Spatial Sound Synthesis (2002) Simulated time response. Frontal plane (response below 5 kHz) Modeling the Torso Algazi, Duda and Thompson, “The use of Head- and-Torso Models for Improved Spatial Sound Synthesis (2002) Model can be implemented computationally. Alternative Approaches Yuvi Kahana, et. Al, Numerical Modelling of the Transfer Functions of a Dummy-Head and of the External Ear (1999) Sound pressure at 2 KHz with sound source at 45degrees in azimuth and 45degrees in elevation. Alternative Approaches Yuvi Kahana, et. Al, Numerical Modelling of the Transfer Functions of a Dummy-Head and of the External Ear (1999) Three snapshots of time domain simulation with wave up to 6.4 kHz. We still lack a comprehensive model of the physical acoustics of the directional hearing system.