* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Process
Heat capacity wikipedia , lookup
Temperature wikipedia , lookup
Heat equation wikipedia , lookup
Equipartition theorem wikipedia , lookup
Calorimetry wikipedia , lookup
Equation of state wikipedia , lookup
Heat transfer wikipedia , lookup
Thermal conduction wikipedia , lookup
Conservation of energy wikipedia , lookup
First law of thermodynamics wikipedia , lookup
Heat transfer physics wikipedia , lookup
Internal energy wikipedia , lookup
Second law of thermodynamics wikipedia , lookup
Chemical thermodynamics wikipedia , lookup
Gibbs free energy wikipedia , lookup
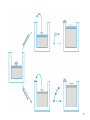
Thermodynamic system wikipedia , lookup
History of thermodynamics wikipedia , lookup
Chemical Thermodynamics 2013/2014 3rd Lecture: Work, Heat and the First Law of Thermodynamics Valentim M B Nunes, UD de Engenharia Introduction As we saw before, thermodynamics it’s a science that studies energy transformations but, as we will see, thermodynamics describes macroscopic properties of equilibrium systems. Although everybody as the feeling of knowing what is energy, it is very difficult to give a precise definition. For our purposes Energy can be defined as the ability to cause changes or realize Work. One of the fundamental laws of nature is the law of conservation of energy. Energy in a system may take on various forms (e.g. kinetic, potential, heat, light) but energy may neither be created nor destroyed. 2 Some basic concepts Thermodynamic System – it’s a part of the Universe that is being studied. Exterior or Surroundings of the system – all the rest of the Universe Boundary of the system – its what divides the system from the rest of the universe. Surroundings System Universe = System + Surroundings 3 Types of systems Isolated System – An isolated system is that in which no transfer of mass & energy takes place across the boundaries of system Closed System - A closed system in which no transfer of mass takes place across the boundaries of system but energy transfer is possible Open System - An open system is one in which both mass & energy transfer takes place across the boundaries 4 Describing Systems To describe a given system we need to indicate the components of the system, their physical state (gas, liquid, solid, mixtures) and the state properties, like pressure, p, volume, V, number of moles, n, mass, m, and temperature, T. 5 Properties of a system When one system suffers a transformation it goes from an initial state to a final state. The properties of the system that are univocally determined by the sate of the system are state functions (or state variables or state properties). These properties may be either intensive or extensive. Extensive properties depends on the size or extension of the system, like the volume, V. Intensive properties are independent of the size of the system, like temperature or pressure. If we divide an extensive property by the number of moles we obtain an intensive property, like the molar volume: V Vm n 6 State of a System at Equilibrium The state of equilibrium is defined by the macroscopic properties and is independent of the history of the system. Cooling Heating 7 Change of state A process or transformation is a change in the state of the system over time, starting with a definite initial state and ending with a definite final state. The process is defined by a path, which is the continuous sequence of consecutive states through which the system passes, including the initial state, the intermediate states, and the final state There are many types of processes to change the state of a system at constant volume (isochoric), at constant pressure (isobaric), at constant temperature (isotherm) and so one.. 8 Infinitesimal Changes An infinitesimal change of the state function X is written dX. The mathematical operation of summing an infinite number of infinitesimal changes is integration, and the sum is an integral. The sum of the infinitesimal changes of X along a path is a definite integral equal to •X: X2 dX X 2 X 1 X X1 If dX obeys this relation—that is, if its integral for given limits has the same value regardless of the path—it is called an exact differential. The differential of a state function is always an exact differential 9 Cycles A cyclic process is a process in which the state of the system changes and then returns to the initial state. In this case the integral of dX is written with a cyclic integral. Since a state function X has the same initial and final values in a cyclic process, X2 is equal to X1 and the cyclic integral of dX is zero: dX 0 10 Internal energy The total energy of a system is the Internal Energy, U. The internal energy is a state function. If a system as an initial energy Ui and after a transformation as a n energy Uf then the variation of internal energy, U is: U U f U i The internal energy is an extensive property, that is, it depends on the size of the system. It can only be changed by two different modes: Work, W, and Heat, Q, trough the boundary of the system. 11 Work and Heat Heat can be viewed as a disordered way of transferring energy (caused by temperature gradient across the boundary) while work is an order way of transferring energy (lifting a weight for instance) 12 The 1st Law of Thermodynamics The internal energy of an isolated system is constant. If the system is closed it can only be transferred by heat flow or work done. In differential form dU dQ dW In integrated form: U Q W dQ and dW are not exact differentials what means that they will depend on the path! So heat and work are path functions, they are associated with a process, not a state. 13 The 1st Law of Thermodynamics An equivalent formulation of the first law is the following: the work necessary to change an adiabatic system from one state to another is always the same, no matter the type of work done. 14 The 1st Law of Thermodynamics But… AU is the same for all the processes! f dU U f U i U i 15 Signal convention Process System does work on the surroundings Surroundings do work to the system Heat absorbed by the system (endothermic process) Heat absorbed by the surroundings (exothermic process) Signal + + - 16 Work p Force Force pext A Area Work Force Dist ance dW pext A dx pext dV dW pext dV 17 Expansion work Let us assume the work done by the expansion of a gas against constant external pressure: W pext dV pext dV pext V f Vi Vf Vf Vi Vi W pext V In a free expansion, against the vacuum, the external pressure is null (pext = 0), so W=0. 18 Isothermal Perfect gas expansion (1 step) 19 Isothermal Perfect gas expansion (two steps) 20 Isothermal Perfect gas expansion (Infinite steps) If at each step we have p = pext, we have infinite expansions, and maximum work is delivered to the surroundings! This is obtained using a reversible path. 21 Reversible Process Considering the reversible expansion of a perfect gas, he have: Vf Wmax, rev pdV Vi Vf Wmax, rev Vi nRT dV V Wmax, rev nRT ln Vf Vi R = 8.314 J.K-1.mol-1 22 23 Summary Process If Pext = 0 If Pext = constant If the expansion is reversible W 0 W pext V W nRT ln Vf Vi 24 Reversible vs Irreversible (T, p1, V1) expansion (T,p2,V2) compression (T,p1,V1) Process I: expansion against pext = p2 and compression with pext = p1 Wcycle Wexp Wcomp p2 V2 V1 p1 V2 V1 Wcycle p1 p2 V2 V1 0 Work done to System! dW 0 Process II: infinite expansions and compressions with pext = p along the path Wcycle nRT ln V2 V nRT ln 1 0 V1 V2 Reversible Process! 25 Heat It’s the quantity flowing between the system and the surroundings that can cause a change in temperature of the system and/or the surroundings. Like work, heat its not a state function! What connects Heat with temperature it’s the Heat capacity, C. Units SI are J.K-1.mol-1. dq CdT At constant volume: At constant pressure: q CV T V q Cp T p 26 Heat Capacity at constant volume At constant volume, dw = 0 so, from the 1st Law, we can easily obtain: U CV T V 27 Enthalpy, H Chemical reactions and many other processes, including biological, take place under constant pressure and reversible pV work. Let us define a new function of state, the enthalpy, defined as: H U pV Differentiating: dH dU pdV Vdp dH dq dw pdV Vdp dH dq pdV pdV Vdp dH dq Vdp At constant pressure: dH dq 28 Heat Capacity at constant pressure Previous result shows that the enthalpy its equal to the heat in a constant pressure process, and we can finally obtain: H Cp T p 29 Relation between Heat Capacity’s for an ideal gas We can now derive a relation between Cp and Cv for an ideal gas: H U C p CV T p T V But, H = U + pV =U + RT (per mole) Assume this is equal! U U C p CV R T T p p C p CV R For instance, for an ideal monatomic gas CV =3/2 R , so Cp = 5/2 R 30 The Joule Experiment U V T Let us consider the free expansion of a gas, to get T Adiabatic, q = 0 Expansion into the vacuum, w = 0 P~0 U 0 The experiment proofs that, for an ideal gas, U = U(T)! 31 Total differential of U If we regard the internal energy function as U =U(V,T) , then the total differential of U comes: U U dU dV dT V T T V For an ideal gas U T 0 so dU = CvdT V T This means that the internal energy of an ideal gas depends only on temperature. As a consequence: ΔU = 0 for all isothermal expansions or compressions of an ideal gas, and U CV dT For any ideal gas change of state. 32