Download Reading Strategies

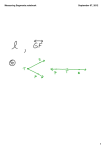
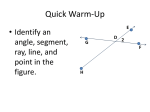
Name ________________________________________ Date __________________ Class__________________
LESSON
1-2
Reading Strategies
Understanding Vocabulary
Consider the following terms:
congruent segments—segments of
the same length
These segments are
not congruent.
midpoint—point at the exact center of a segment
bisect—dividing into two congruent parts
segment bisector—any ray, segment, or line that intersects a segment at its midpoint
Use the figure for Exercises 1–3.
1. Name the congruent segments
in this figure.
________________________________________________________________________________________
2. Name the midpoint of BC . _____________________
3. Name the segment bisector of BC . __________________
Use the figure for Exercises 4–6.
4. Name the congruent segments
in this figure.
________________________________________________________________________________________
5. Name the midpoint of ZY . ____________________
6. Name the segment bisector of ZY . __________________
Original content Copyright © by Holt McDougal. Additions and changes to the original content are the responsibility of the instructor.
1-18
Holt McDougal Geometry
Reading Strategies
Reteach
1. 4 cm
2. 1.5 cm
3. 3 cm
4. 2
5. 6
6. 41
7. 21
8. 135
9. 22
1. AB,CD; BC, AD; AC, BD; DE, BE,CE, and AE
2. Point E
3. AD
4. XY ≅ XZ; ZP ≅ PY
5. Point P
6. XP
10.
1-3 MEASURING AND CONSTRUCTING
11.
12.
13. NP or PN .
14. 4
ANGLES
Practice A
15. 12, 12, 24
Challenge
1. Possible drawing:
1. vertex
JJJG
JJJG
2. PQ and PR
3. ∠QPR and ∠RPQ
4. point S
5. protractor
6. 90°; right
7. 60°; acute
8. 180°; straight
9.
10. 125°
2. Check students’ work.
Practice B
2
of the distance from
3
each vertex to the midpoint of the
opposite side.
3. The centroid is
4. EN = 2 cm, EX = 3 cm,
1.
2
of 3 cm is 2
3
2
EX; FN = 2 cm,
3
2
FY = 3 cm, therefore FN = FY; GN = 2
3
2
cm, GW = 3 cm, therefore GN = GW
3
cm, therefore EN =
2. ∠A, ∠C, ∠ABC, ∠ABD, ∠ADB, ∠ADC,
∠CBD, and ∠CDB
Problem Solving
3
1. 24 ft
4
4. 120°; obtuse
5. 30°; acute
6. 14°
7. 123°
8. 44°
9. 3°15′05″
2. 23 ft
10. 79.958°
Practice C
1. ∠BAE
3. 18 ft
2. ∠BAC, ∠DAE, ∠CAD
4. 9.7 cm and 38.8 cm
5. B
3. 90°; right
3. ∠BAD and ∠CAE
6. F
4. a straight angle
7. D
5. First, Keisha can draw a straight angle
(180°). She can then bisect the straight
angle to make two right angles (90°).
Keisha can then bisect one of the right
angles to make a 45° angle.
Original content Copyright © by Holt McDougal. Additions and changes to the original content are the responsibility of the instructor.
A3
Holt McDougal Geometry