Download Exploring Congruent Triangles

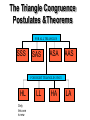
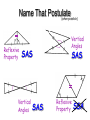
Exploring Congruent Triangles
CCSS
G-CO.7
Use the definition of congruence in terms of rigid motions to show that two triangles
are congruent if and only if corresponding pairs of sides and corresponding pairs of
angles are congruent
G-CO.8
Explain how the criteria for triangle congruence (ASA, SAS, and SSS) follow from
the definition of congruence in terms of rigid motions.
Student will be able to Apply the concepts of congruency by solving
problems on or off a coordinate plane; or solves problems using congruency
involving problems within mathematics or across disciplines or contexts.
Congruent triangles: Triangles that are
the same size and the same shape.
C
A
F
B
D
In the figure
E
DEF 
ABC
Congruence Statement: tells us the order in
which the sides and
angles are congruent
If 2 triangles are congruent:
The congruence statement tells us which
parts of the 2 triangles are
corresponding “match up”.
ABC  DEF Means
3 Angles:
A  D, B  E, C  F
and
3 Sides:
AB  DE, BC  EF, andAC  DF
ORDER IS VERY IMPORTANT
Example
C
A
In the figure
R
F
T
TEF 
E
ARC
A  T, R  E, C  F
AR  TE, RC  EF, AC  TF
Example 2
Congruent Triangles
A
Z
B
C X
Example 3
JKL  RST
Write the Congruence Statement
ABC  ZXY
Y
R
J  ______
K
S  ______
ST
KL  ______
Example 3 : Congruence
Statement
Finish the following congruence statement:
ΔJKL  Δ_N M
_ _L
M
J
L
K
N
Definition of Congruent: Two triangles are congruent
Triangles
if and only if their
(CPCTC)
corresponding parts are
congruent. (tells us when
Triangles are congruent)
Are the 2 Triangles Congruent. If so write
The congruence statement.
Ex. 2
Are these 2 triangles congruent? If so, write a congruence statement.
Reflexive Property
Does the Triangle on the left have any
of the same sides or angles as the
triangle on the right?
SSS - Postulate
If all the sides of one triangle are congruent to all
of the sides of a second triangle, then the triangles
are congruent. (SSS)
Example #1 – SSS – Postulate
Use the SSS Postulate to show the two triangles
are congruent. Find the length of each side.
AC = 5
BC = 7
2
2
AB = 5  7  74
MO = 5
NO = 7
MN =
52  72  74
ACB  MON
By SSS
Definition – Included Angle
J
 K is the angle between
JK and KL. It is called the
included angle of sides JK
and KL.
K
L
J
What is the included angle
for sides KL and JL?
L
K
L
SAS - Postulate
If two sides and the included angle of one triangle
are congruent to two sides and the included angle
of a second triangle, then the triangles are
congruent. (SAS)
S
L
Q
P
A
S
A
J
S
S
K
JKL  PQR
by SAS
R
Definition – Included Side
J
JK is the side between
 J and  K. It is called the
included side of angles J
and K.
K
L
J
What is the included side
for angles K and L?
KL
K
L
ASA - Postulate
If two angles and the included side of one triangle
are congruent to two angles and the included side
of a second triangle, then the triangles are
congruent. (ASA)
J
X
Y
K
L
JKL  ZXY by ASA
Z
Identify the Congruent Triangles.
Identify the congruent triangles (if any). State the
postulate
by which the triangles are congruent.
A
J
R
B
C
H
I
S
K
M
O
L
P
VABC VSTR by SSS
VPNO VVUW by SAS
N V
T
U
W
Note: VJHI is not
SSS, SAS, or ASA.
AAS (Angle, Angle, Side)
• If two angles and a nonincluded side of one triangle
are congruent to two angles
and the corresponding non- C
included side of another
triangle, . . .
then
the 2 triangles are
CONGRUENT!
A
D
B
F
E
HL (Hypotenuse, Leg)
***** only used with right triangles****
• If both hypotenuses and a
pair of legs of two RIGHT
triangles are congruent, . . .
A
C
B
D
then
the 2 triangles are
CONGRUENT!
F
E
The Triangle Congruence
Postulates &Theorems
FOR ALL TRIANGLES
SSS
SAS
ASA
AAS
FOR RIGHT TRIANGLES ONLY
HL
Only
this one
is new
LL
HA
LA
Summary
• Any Triangle may be proved congruent by:
(SSS)
(SAS)
(ASA)
(AAS)
• Right Triangles may also be proven congruent by HL (
Hypotenuse Leg)
• Parts of triangles may be shown to be congruent by
Congruent Parts of Congruent Triangles are Congruent
(CPCTC).
Example 1
Given the informatio n in the diagram,
is there any way to determine if
A
CB  DF ?
C
B
D
YES!! CAB  DEF by SAS
so CB  DF by CPCTC
E
F
Example 2
A
C
B
D
E
F
• Given the markings on
the diagram, is the pair
of triangles congruent
by one of the
congruency theorems in
this lesson?
No ! SSA doesn’t work
Example 3
A
C
D
• Given the markings on
the diagram, is the pair
of triangles congruent by
one of the congruency
theorems in this lesson?
B
YES ! Use the
reflexive side CB,
and you have SSS
Name That Postulate
(when possible)
SAS
SSA
ASA
SSS
Name That Postulate
(when possible)
AAA
SAS
ASA
SSA
Name That Postulate
(when possible)
Reflexive
Property
SAS
Vertical
Angles
SAS
Vertical
Angles
SAS
Reflexive
Property
SSA
Let’s Practice
Indicate the additional information needed
to enable us to apply the specified
congruence postulate.
For ASA:
B  D
For SAS:
AC  FE
For AAS:
A  F
Homework Assignment
Castlelearning