Download Geometry 12.2 ‐ chords and arcs A. Chord A chord is a segment

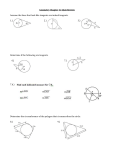
Geometry
12.2 ‐ chords and arcs
A.
Chord
A chord is a segment whose endpoints are on a circle
Theorem 12 ‐ 4: Within a circle or congruent circles
(a)
Congruent central angles have congruent chords
(b)
Congruent chords have congruent arcs
(c)
Congruent arcs have congruent central angles
Example 1: In the diagram, radius OX bisects angle AOB. What can you conclude
A
X
O
B
Mar 22­8:37 AM
1
B. Theorem 12 ‐ 5: Within a circle or congruent circles
(a) Chords equidistant from the center are congruent
(b) Congruent chords are equidistant from the center
C. More Theorems
(a) Theorem 12 ‐ 6: In a circle, a diameter that is perpendicular to a chord bisects the chord and its arcs
(b) Theorem 12 ‐ 7: In a circle, a diameter that bisects a chord is perpendicular to the chord
(c) Theorem 12 ‐ 8: In a circle, the perpendicular bisector of a chord contains the center of the circle
Mar 22­8:40 AM
2
D. Examples. Find the value of x.
3.
2. 4. 18
x
18 16
x
4
36
7
4
7
7
3
7
3
x
x
Mar 22­8:41 AM
3
6.
5.
x
2
7.
24 ft
x
5 ft
2 cm
5 cm
3
x
Mar 22­8:47 AM
4
Try these examples at your seats
Find Radius Only
Feb 3­2:04 PM
5
Try these at your seats as well
(Honors Geometry Only)
Feb 3­2:20 PM
6
E. Conclusions. Feb 3­2:22 PM
7
12.2 HW p. 673 numbers 1 ­ 18 all, 19, 21, 30 ­ 32, 49, 50 May 6­11:12 AM
8