Download Chapter 8: Introduction to Functions

Chapter 8: Introduction to Functions
Algebra I
Name _____________________
Date ______________________
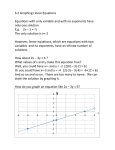
8.1 Equations in Two Variables
1. (2, -3), (a, b) and (x, y) are examples of ordered pairs. Ordered pairs always occur in
alphabetical order.
2. When an ordered pair of numbers makes an equation true, this ordered pair is called a solution of
an equation in two variables.
3. In the ordered pair (3, 5), 3 is the x-value and 5 is the y-value.
4. State whether each ordered pair is a solution of the given equation.
a) 2x + y = 6; (1, 4)
b) 3a – 2b = 6; (5, 3)
8.2 Points, Lines and Their Graphs
On the grid to the right, label the following:
Horizontal Axis
Origin
Vertical Axis
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
x-axis
y-axis
Positive x-axis
Positive y-axis
Negative x-axis
Negative y-axis
Coordinate
1. Plot each point on the coordinate grid.
a) (-3, 2)
b) (-1, -3)
8.3 Slope of A Line
SLOPE
1. Slope is defined as: ______________ or ___________________.
2. The formula for finding slope is: ________________________.
3. A line can have a ___________________ slope, a ____________________ slope,
a slope of _______________ or _____________________.
4. Lines with these different slopes look like:
positive
negative
zero
no slope
5. State each slope as positive, negative, zero or no slope:
a.
b.
c.
d.
6. Find the slope of each of the following:
a.
b.
c.
7. Using the formula, find the slope of the lines that contain the following points:
a. (1, 6), (3, -2)
b. (-2, 3), (4, 8)
c. (7, -6), (-5, 2)
8. To find the slope of a line given an equation of the line you must find __________ points on the
line. To find two points, first let x = _________ and find the value of ________. Second, let y =
_______ and find the value of __________. This will give you two points on the line. Then use
the formula to find the slope.
a. 2x + 4y = 12
b. 6x – 2y = 12
c. 2x + 5y = 10
8.4 The Slope-Intercept Form of a Linear Equation
1. To draw a line through a given point with a given slope, first you have to __________ the point.
Second, use the ___________ to find another point on the line. Then ____________ the two points.
a. P(-2, 1 ) slope = -3
b. P(1, 1) slope = -1
SLOPE-INTERCEPT FORM
1. The slope-intercept form of an equation is ___________________________.
2. m = ___________________
b = ______________________
3. If an equation of a line is of the form y = mx , the y-intercept is ____________.
4. Give the slope and y-intercept of each line.
a. y = 2x + 8
b. y = -5x -3
c. y = 5 - ½ x
d. y = (-2/3)x - 9
e. y = (1/5)x
f. y = 5
5. To graph an equation using the slope and y-intercept, first graph the ________________. Then
use the ________________ to find another point on the line. Finally, _____________ the two
points.
6. Graph each equation using slope and y-intercept.
a. y = 3x – 4
b. y = -(4/5)x + 2
c. 2x – y = -4
d. x + 5y = 5
PARALLEL and PERPENDICULAR LINES
1. When two lines are parallel they ______________________________.
2. When two lines are parallel their slopes are _____________________.
3. When two lines are perpendicular they ____________ at a ______________.
4. When two lines are perpendicular their slopes are _____________________________.
5. The opposite reciprocal of 0 is _________________, giving the line ______________.
6. Find the slope of a line parallel to 3x – 5y = 110.
7. Find the slope of a line perpendicular to x – 3y – 8 = 0
8. Show whether the graphs of each pair of equations are parallel, perpendicular or neither.
a. 3x + 6y = 8
y = 2x – 8
c. 3x + y = 7
y = -3x + 6
b. x – 2y = 1
-2x + 5y = 9
d. ½ x + ½ y = 5
2x + 2y = 3
8.5 Determining the Equation of the Line
Write an equation in slope-intercept form of each line described.
Example 1
slope -3; y-intercept 4
Example 2
slope
2
3
; y-intercept 9
Example 3
slope  13 ; x-intercept 3
Example 4
slope 3; passes through (4,1)
Example 5
slope  52 ; passes through (5, 7)
Example 6
slope 0; passes through (-5, 4)
Example 7
Contains (0,3), (2, -1)
Example 8
Contains (-1, -2), (0, 3)
Example 9
Contains (-2, 4), (4, 2)
Example 10
y-intercept -5; x-intercept 3
Example 11
horizontal line through (-2, -1)
8.5 Supplement: Point-Slope Form
Slope-intercept form of an equation is _______________, where m = _______ and b = _________.
Another form of an equation is point-slope form. The equation for point-slope form is
__________________, where (x1, y1) represents ______________ and m = ________.
Example 1 Given a point and the slope of a line, write an equation in point-slope form.
a. (5, 4) ; slope is 6
b. (-2, 5); slope is 23
c. (-1, -6); slope is  12
Example 2 An equation of a line is y - 4 = - 34 (x + 6). Identify the point and slope used in the equation.
Example 3 Write an equation in point-slope form for the line described.
a. The line through (2, 5) that is perpendicular to the line y = 43 x + 1
b. The line through (-7, 6) that is parallel to the line 4x + 2y = 9
Example 4 Transfer y + 3 =
1
2
(x – 4) to slope-intercept form.
8.6 Functions Defined by Tables and Graphs
Use the glossary in your textbook to define the following:
Domain:
Range:
Relation:
Function:
Every _________ is a __________, but not every ____________ is a ______________.
When writing an ordered pair the __________ comes first, then the ___________.
The following is an example of a function:
George Washington
February 22
Marie Curie
November 7
Charles Darwin
February 12
Abraham Lincoln
Domain: {people}
Range: {Birth date}
Write the previous function as a list of ordered pairs:
Example 1 The table below shows the amount of rainfall in Center City for a six-month period.
Month
January
February
March
April
May
June
Rainfall
(mm)
12
15
21
47
52
39
b. Draw a bar graph for the function.
a. Write each paring as a list of ordered pairs.
c. Draw a broken-line graph for the function.
Example 2 The following represents the average weekly pay for the average American in the United
States.
Year
1960
1965
Average weekly
$88
$122
pay
a. State the domain and range.
1970
$190
1975
$289
1980
$371
1985
$386
b. Write each pairing as ordered pairs.
c. Draw a bar graph for the function.
d. Draw a broken-line graph for the function.
8.7 Functions Defined by Equations
P(n) = 5n – 500 is an example of ____________ _______________.
g(2) = 6 is read “g of 2 equals 6” or “the value of g at 2 is 6”
Example 1 List the range of each function under the given domain.
a. F(x) = 5x – 4, D = {-1, 2, 3}
x
-1
2
3
5x - 4
R={
}
b. Q(n) = 4n – 3, D = {0, 2, 3}
c. h(x) = 3y + 1, D = {-3, 0, 1}
Example 2 Find the values for each given function with the set of real numbers as the domain.
a. R(t) = t + 2 for R(2)
b. G(n) = n – 3 for G(-3)
c. f(x) = 3x -2 for f(-2)
d. p(x) = 4 – 2x for p(0)