Download Probability

Conditional Probability
Brian Carrico
Nov 5, 2009
What is Probability?

Predicting a random event
–

A random event is one in which individual
outcomes are uncertain but the long-term pattern
of many individual outcomes is predictable and
every possible outcome can be described prior to
its performance
We can use the long-term patterns to predict
individual outcomes
What is Conditional Probability?


In some situations current or previous
conditions have an impact on the probability
Examples:
–
–
–
–
Weather
Stock Market
Genetics
Card games
What sort of factors can impact
probability?

What is the probability of rolling an even
number on a fair six-sided die?
–

What if you’re told the roll was less than 4?
–

1/2
1/3
How did you come up with that?
Basic Formula for Conditional
Probability
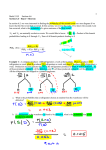
 P(A|B)

= P(A∩B)
P(B)
Some Practice
Female
Male
Dem
21
18
Rep
18
24
Ind
8
11
Total
47
53
Total
39
42
19
100




P(Female)
P(Female|Democrat)
P(Republican)
P(Republican|Male)




47/100 = 0.47
21/39 = 0.538
42/100 = 0.42
24/53 = 0.453
Law of Total Probability

If A is some event and {B1, B2, … Bn} forms a
partition of the sample space then:
 P(A)=ΣP(A|Bi)*P(Bi)
Proving P(A)=ΣP(A|Bi)*P(Bi)






U{B1, B2,…, Bn} = S
P(A) = P(A∩S)
P(A) = P(A∩(U{B1, B2,…, Bn} ))
P(A) = P(U{A∩B1, A∩B2,…, A∩Bn})
P(A) = ΣP(A∩Bi)
P(A) = ΣP(A|Bi)*P(Bi)
Using the Law of Total Probability

Suppose you have two urns containing balls
colored green and red. Urn I contains 4
green balls and 6 red balls, Urn II contains 6
green balls and 3 red balls. A ball is moved
from Urn I to Urn II at random then a ball is
drawn from Urn II. Find the probability that
the ball drawn from Urn II is green.
Urn Problem Continued

Events:
–
–
–


G1=Ball transferred from Urn I to Urn II is Green
R1=Ball transferred from Urn I to Urn II is Red
G2=Ball drawn from Urn II is Green
We want P(G2)
We have
–
–
–
P(G2)= P(G2|G1)*P(G1) + P(G2|R1)*P(R1)
P(G2)=(7/10)*(4/10) + (6/10)*(6/10)
P(G2)=28/100+36/100=64/100
Bayes’ Rule

If A is some event and {B1, B2, … Bn} forms a
partition of the sample space then:
 P(Bj|A)=

_P(A|Bj)*P(Bj)
ΣP(A|Bi)*P(Bi)
Using Bayes’ Rule


You are tested for a disease that occurs in
0.1% of the population. Your physician tells
you that the test is 99% accurate. If the test
comes back positive, what is the probability
that you have the disease?
Events:
–
T=positive test
D=you have the disease
Test result continued

Given Probabilities:
–


P(D)=0.001
P(T|D)=0.99
P(T|Dc)=0.01
We want P(D|T)
From Bayes’ Rule we know
–
–
–
P(D|T)=
P(T|D)*P(D)
___
P(T|D)*P(D)+ P(T|Dc)*P(Dc)
P(D|T)=
(0.99*0.001)
_
(0.99*0.001)+(0.01*0.999)
P(D|T)=0.09
Testing Independence



If A and B are two independent events then
P(A|B)=P(A)
Using formulas from earlier we can see that
P(A|B)=P(A∩B)=P(A)
P(B)
So, P(A∩B)=P(A)*P(B)
A test of Independence

A fair coin is tossed twice. Are the following
events independent?
–



A= 1st toss lands heads
B= 2nd toss lands heads
S={HH,HT,TH,TT}
P(A)=1/2 P(B)=1/2 P(A∩B)=1/4
P(A)*P(B)=1/2*1/2=1/4=P(A∩B)
Homework
Sources

Probability Models by John Haigh 2002

Probability by Larry Leemis 2009