Download Mechanical Vibrations

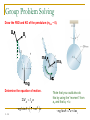
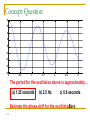
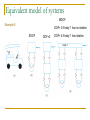
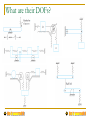
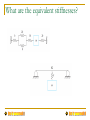
Introduction
Mechanical Vibrations
What is vibration?

Vibrations are oscillations of a system about
an equilbrium position.
Vibration…
It is also an
everyday
phenomenon we
meet on
everyday life
Vibration …
Useful Vibration
Harmful vibration
Compressor
Noise
Testing
Destruction
Wear
Ultrasonic
cleaning
Fatigue
Vibration parameters
All mechanical systems
can be modeled by
containing three basic
components:
spring, damper, mass
When these components are subjected to constant force,
they react with a constant
displacement, velocity and acceleration
Free vibration


When a system is initially disturbed by a displacement,
velocity or acceleration, the system begins to vibrate with
a constant amplitude and frequency depend on its
stiffness and mass.
This frequency is called as natural frequency, and the
form of the vibration is called as mode shapes
Equilibrium pos.
Forced Vibration
If an external force applied to a
system, the system will follow the
force with the same frequency.
’
However, when the force
frequency is increased to the
system’s natural frequency,
amplitudes will dangerously
increase in this region. This
phenomenon called as
“Resonance”
Watch these …
Bridge collapse:
http://www.youtube.com/watch?v=j-zczJXSxnw
Hellicopter resonance:
http://www.youtube.com/watch?v=0FeXjhUEXlc
Resonance vibration test:
http://www.youtube.com/watch?v=LV_UuzEznHs
Flutter (Aeordynamically induced vibration) :
http://www.youtube.com/watch?v=OhwLojNerMU
Modelling of vibrating systems
Lumped (Rigid) Modelling
Numerical Modelling
Element-based
methods
(FEM, BEM)
Statistical and Energybased methods
(SEA, EFA, etc.)
Because running in the International Space
Station might cause unwanted vibrations, they
have installed a Treadmill Vibration Isolation
System.
2 - 10
• Mechanical vibration is the motion of a particle or body which
oscillates about a position of equilibrium. Most vibrations in
machines and structures are undesirable due to increased stresses
and energy losses.
• Time interval required for a system to complete a full cycle of the
motion is the period of the vibration.
• Number of cycles per unit time defines the frequency of the vibrations.
• Maximum displacement of the system from the equilibrium position is the
amplitude of the vibration.
• When the motion is maintained by the restoring forces only, the vibration
is described as free vibration. When a periodic force is applied to the
system, the motion is described as forced vibration.
• When the frictional dissipation of energy is neglected, the motion
is said to be undamped. Actually, all vibrations are damped to
some degree.
19 - 11
Free Vibrations of Particles. Simple
• If a particle is displaced through a distance x from its
Harmonic Motion
equilibrium position and released with no velocity, the
m
particle will undergo simple harmonic motion,
ma  F  W  k  st  x   kx
mx  kx  0
• General solution is the sum of two particular solutions,
 k 
 k 
x  C1 sin 
t   C 2 cos
t 
 m 
 m 
 C1 sin  n t   C 2 cos n t 
• x is a periodic function and n is the natural circular
frequency of the motion.
• C1 and C2 are determined by the initial conditions:
19 - 12
x  C1 sin  nt   C2 cos nt 
C2  x0
v  x  C1 n cos nt   C2 n sin  nt 
C1  v0  n
Free Vibrations of Particles. Simple
Harmonic Motion
x  xm sin  nt   
xm 
v0  n 2  x02 
amplitude
  tan 1 v0 x0 n   phase angle
n 
fn 
19 - 13
2
n
1
n
 period

n
 natural frequency
2
Free Vibrations of Particles. Simple
• Velocity-time and acceleration-time curves can be
Harmonic Motion
represented by sine curves of the same period as the
displacement-time curve but different phase angles.
x  xm sin  nt   
v  x
 xm n cos n t   
 xm n sin  n t     2
a  x
  xm n2 sin  n t   
 xm n2 sin  n t     
19 - 14
Simple Pendulum (Approximate
• Results obtained for the spring-mass system can be
Solution)
applied whenever the resultant force on a particle is
proportional to the displacement and directed towards
the equilibrium position.
• Consider tangential components of acceleration and
force for a simple pendulum,
 Ft  mat :  W sin   ml
g


  sin   0
l
for small angles,
g
l
    0
   m sin  n t   
n 
19 - 15
2
n
 2
l
g
Simple Pendulum (Exact Solution)
g
l
An exact solution for
  sin   0
leads to
l  2
d
n  4

g 0 1  sin 2  2  sin 2 
m
which requires numerical solution.
n 
19 - 16
2K 
l
 2

 
g
Concept Question
The amplitude of a
vibrating system is
shown to the right.
Which of the
following statements
is true (choose
one)?
a) The amplitude of the acceleration equals the
amplitude of the displacement
b) The amplitude of the velocity is always opposite
(negative to) the amplitude of the displacement
c) The maximum displacement occurs when the
acceleration amplitude is a minimum
d) The phase angle of the vibration shown is zero
2 - 17
Sample Problem 19.1
SOLUTION:
• For each spring arrangement, determine
the spring constant for a single
equivalent spring.
• Apply the approximate relations for the
harmonic motion of a spring-mass
system.
A 50-kg block moves between vertical
guides as shown. The block is pulled
40mm down from its equilibrium position
and released.
For each spring arrangement,
determine a) the period of the vibration,
b) the maximum velocity of the block,
and c) the maximum acceleration of the
block.
19 - 18
Sample Problem 19.1
k1  4 kN m k2  6 kN m
SOLUTION:
• Springs in parallel:
- determine the spring constant for equivalent spring
- apply the approximate relations for the harmonic
motion of a spring-mass system
k
104 N/m
n 

 14.14 rad s
m
20 kg
n 
P  k1  k2
k
P

2
n
vm  x m  n
 0.040 m 14.14 rad s 
 k1  k2
 10 kN m  10 N m
4
vm  0.566 m s
am  x m an2
 0.040 m 14.14 rad s 2
19 - 19
 n  0.444 s
am  8.00 m s 2
Sample Problem 19.1
k1  4 kN m k2  6 kN m
• Springs in series:
- determine the spring constant for equivalent spring
- apply the approximate relations for the harmonic
motion of a spring-mass system
n 
n 
k
2400N/m

 6.93 rad s
m
20 kg
2
n
 n  0.907 s
vm  x m  n
P  k1  k2
k
P

 k1  k2
 10 kN m  104 N m
19 - 20
 0.040 m 6.93 rad s 
vm  0.277 m s
am  x m an2
 0.040 m 6.93 rad s 2
am  1.920 m s 2
Free Vibrations of Rigid Bodies
• If an equation of motion takes the form
x   n2 x  0 or    n2  0
the corresponding motion may be considered
as simple harmonic motion.
• Analysis objective is to determine n.
• Consider the oscillations of a square plate
 W b sin    mb  I


1 m 2b 2  2b 2  2 mb 2 , W  mg
but I  12
3
3g
3g
 
sin    
 0
5b
5b
3g
2
5b
then  n 
, n 
 2
5b
n
3g
• For an equivalent simple pendulum,
19 - 21
l  5b 3
Sample Problem 19.2
SOLUTION:
k
• From the kinematics of the system, relate
the linear displacement and acceleration
to the rotation of the cylinder.
• Based on a free-body-diagram equation
for the equivalence of the external and
effective forces, write the equation of
motion.
A cylinder of weight W is suspended as • Substitute the kinematic relations to arrive
shown.
at an equation involving only the angular
displacement and acceleration.
Determine the period and natural
frequency of vibrations of the cylinder.
19 - 22
Sample Problem 19.2
SOLUTION:
• From the kinematics of the system, relate the linear
displacement and acceleration to the rotation of the
x  r
  2 x  2r
cylinder.

 


 
a  r  r
a  r
• Based on a free-body-diagram equation for the
equivalence of the external and effective forces, write
the equation
 M Aof motion.
 M A eff :
Wr  T2 2r   ma r  I
but T2  T0  k  12 W  k 2r 
• Substitute the kinematic relations to arrive at an
equation involving only the angular displacement and
acceleration.
Wr  1 W  2kr 2r   mrr  1 mr 2
2
 
2
8k
 0
3m
8k
n 
3m
19 - 23

n 
2
n
 2
3m
8k
fn 
 n 1 8k

2 2 3m
Sample Problem 19.3
SOLUTION:
• Using the free-body-diagram equation for
the equivalence of the external and
effective moments, write the equation of
motion for the disk/gear and wire.
W  20 lb
 n  1.13 s
 n  1.93 s
• With the natural frequency and moment of
inertia for the disk known, calculate the
torsional spring constant.
The disk and gear undergo torsional
vibration with the periods shown.
• With natural frequency and spring
Assume that the moment exerted by the constant known, calculate the moment of
wire is proportional to the twist angle.
inertia for the gear.
Determine a) the wire torsional spring
• Apply the relations for simple harmonic
constant, b) the centroidal moment of
motion to calculate the maximum gear
inertia of the gear, and c) the maximum
velocity.
angular velocity of the gear if rotated
through 90o and released.
19 - 24
Sample Problem 19.3
W  20 lb
 n  1.13 s
 n  1.93 s
SOLUTION:
• Using the free-body-diagram equation for the
equivalence of the external and effective moments,
write the equation of motion for the disk/gear and
wire.  M O   M O  :
 K   I 
eff
K
    0
I
n 
K
I
n 
2
n
 2
I
K
• With the natural frequency and moment of inertia for
the disk known, calculate the torsional spring
constant.
2
1
20
8




2
I  12 mr 2  
   0.138 lb  ft  s
2  32.2  12 
1.13  2
19 - 25
0.138
K
K  4.27 lb  ft rad
Sample Problem 19.3
• With natural frequency and spring constant
known, calculate the moment of inertia for the
gear.
I
1.93  2
I  0.403 lb  ft  s2
4.27
W  20 lb
 n  1.13 s
• Apply the relations for simple harmonic motion to
calculate the maximum gear velocity.
 n  1.93 s
  m sin nt
  mn sin nt
m  mn
m  90  1.571 rad
K
I
n 
n 
2
n
 2
K  4.27 lb  ft rad
19 - 26
I
K
 2 
2 
  1.571 rad


1
.
93
s


 n
m   m 
m  5.11rad s
Group Problem Solving
SOLUTION:
• Using the free-body and kinetic diagrams,
write the equation of motion for the
pendulum.
• Determine the natural frequency and
moment of inertia for the disk (use the
small angle approximation).
• Calculate the period.
A uniform disk of radius 250 mm is
attached at A to a 650-mm rod AB of
negligible mass which can rotate freely
in a vertical plane about B. If the rod is
displaced 2°from the position shown
and released, determine the period of
the resulting oscillation.
19 - 27
Group Problem Solving
Draw the FBD and KD of the pendulum (mbar ~ 0).
Bn
Bt

l
r
man
mat
I
mg
Determine the equation of motion.
M B  I B


mgl sin   I  ml 2 
2 - 28
*Note that you could also do
this by using the “moment” from
at, and that at = l
mgl sin   I   lmat
Group Problem Solving
Find I, set up equation of motion
using small angle approximation


mgl sin   I  ml 2 
I 
1 2
mr , sin   
2
1 2
2
mr

ml
2
  mgl  0


Determine the natural frequency
n2 

gl
r2
2
 l2

(9.81)(0.650)

2
2
1
(0.250)

(0.650)
2
2 - 29
 14.053
n  3.7487 rad/s
Calculate the period
n 
2
n
 1.676 s
 n  1.676 s
Concept Question
In the previous problem, what
would be true if the bar was
hinged at A instead of welded
at A (choose one)?
a) The natural frequency of the oscillation would be larger
b) The natural frequency of the oscillation would be larger
c) The natural frequencies of the two systems would be
the same
19 - 30
Principle of Conservation of Energy
• Resultant force on a mass in simple harmonic motion
is conservative - total energy is conserved.
T V  constant
1 mx 2
2
2
 12 kx 2  constant
x   n2 x 2 
• Consider simple harmonic motion of the square plate,
T1  0


V1  Wb 1  cos   Wb 2 sin 2  m 2
 12 Wb  m2
2
T2  12 mvm2  12 I  m
2
 12 mbm   12
 12
53 mb2 m2
23 mb2  m2
V2  0
T1  V1  T2  V2
0  12 Wb  m2  12
19 - 31
53 mb2  m2 n2  0
 n  3g 5b
Sample Problem 19.4
SOLUTION:
• Apply the principle of conservation of
energy between the positions of maximum
and minimum potential energy.
• Solve the energy equation for the natural
frequency of the oscillations.
Determine the period of small
oscillations of a cylinder which rolls
without slipping inside a curved
surface.
19 - 32
Sample Problem 19.4
SOLUTION:
• Apply the principle of conservation of energy
between the positions of maximum and minimum
potential energy.
T1  V1  T2  V2
T1  0
V1  Wh  W R  r 1  cos 

 W R  r   m2 2

V2  0
2
T2  12 mvm2  12 I  m
 12 mR  r m2  12
 34 mR  r 2m2
19 - 33


2
1 mr 2  R  r   2

 m
2
 r 
Sample Problem 19.4
• Solve the energy equation for the natural frequency
of the oscillations.

T1  0
V1  W R  r   m2 2
T2  34 mR  r 2m2
V2  0
T1  V1  T2  V2
0  W R  r 
mg R  r 
 n2 
19 - 34
 m2
2
 m2
2
2 g
3 Rr
 34 m R  r 2m2  0
 34 m R  r 2  m n 2m
n 
2
n
 2
3 Rr
2 g

Forced Vibrations
Forced vibrations - Occur
when a system is subjected to
a periodic force or a periodic
displacement of a support.
 f  forced frequency
 F  ma :


Pm sin  f t  W  k  st  x   mx
W  k  st  x   m sin  f t  mx
mx  kx  Pm sin  f t
mx  kx  k m sin  f t
19 - 35
Forced Vibrations
x  xcomplementary  x particular
 C1 sin  n t  C2 cos n t   xm sin  f t
Substituting particular solution into governing equation,
 m 2f xm sin  f t  kxm sin  f t  Pm sin  f t
xm 
Pm k
m


k  m 2f 1   f  n 2 1   f  n 2
Pm




mx  kx  Pm sin  f t
mx  kx  k m sin  f t
At f = n, forcing input is in
resonance with the system.
19 - 36
Concept Question
A small trailer and its load have
a total mass m. The trailer can
be modeled as a spring with
constant k. It is pulled over a
road, the surface of which can
be approximated by a sine
curve with an amplitude of 40
mm and a wavelength of 5 m.
Maximum vibration amplitude
occur at 35 km/hr. What
happens if the driver speeds up
to 50 km/hr?
a) The vibration amplitude remains the same.
b) The vibration amplitude would increase.
c) The vibration amplitude would decrease.
2 - 37
Sample Problem 19.5
SOLUTION:
• The resonant frequency is equal to the
natural frequency of the system.
• Evaluate the magnitude of the periodic
force due to the motor unbalance.
Determine the vibration amplitude from
the frequency ratio at 1200 rpm.
A motor weighing 350 lb is supported by
four springs, each having a constant 750
lb/in. The unbalance of the motor is
equivalent to a weight of 1 oz located 6
in. from the axis of rotation.
Determine a) speed in rpm at which
resonance will occur, and b) amplitude of
the vibration at 1200 rpm.
19 - 38
Sample Problem 19.5
SOLUTION:
• The resonant frequency is equal to the natural
frequency of the system.
m
W = 350 lb
k = 4(350
lb/in)
350
 10.87 lb  s2 ft
32.2
k  4750  3000 lb in
 36,000 lb ft
k
36,000

m
10.87
 57.5 rad/s  549 rpm
n 
Resonance speed = 549
rpm
19 - 39
Sample Problem 19.5
• Evaluate the magnitude of the periodic force due to the
motor unbalance. Determine the vibration amplitude
from the frequency ratio at 1200 rpm.
 f    1200 rpm  125.7 rad/s

1
 1 lb 
  0.001941 lb  s 2 ft
m  1 oz 

 16 oz  32.2 ft s 2 
W = 350 lb
k = 4(350
lb/in)

 57.5 rad/s
Pm  man  mr 2
 
6 125.7 2  15.33 lb
 0.001941 12
n
xm 
Pm k
1   f  n 2

15.33 3000
1  125.7 57.52
 0.001352 in
xm = 0.001352 in. (out of
phase)
19 - 40
Damped Free Vibrations
• All vibrations are damped to some degree by
forces due to dry friction, fluid friction, or internal
friction.
• With viscous damping due to fluid friction,
 F  ma :
W  k  st  x   cx  mx
mx  cx  kx  0
• Substituting x = elt and dividing through by elt
yields the characteristic equation,
ml2  cl  k  0
2
c
k
 c 
l
 


2m
m
 2m 
• Define the critical damping coefficient such that
2
k
 cc 

  0
m
 2m 
19 - 41
cc  2m
k
 2m n
m
Damped Free Vibrations
• Characteristic equation,
2
c
k
 c 
l
 


2m
m
 2m 
ml2  cl  k  0
cc  2m n  critical damping coefficient
• Heavy damping: c > cc
x  C1e l1t  C2 e l2t
- negative roots
- nonvibratory motion
• Critical damping: c = cc
x  C1  C 2t  e  nt
- double roots
- nonvibratory motion
• Light damping: c < cc
x  e c 2m t C1 sin  d t  C2 cos d t 
2
d  n
19 - 42
c
1     damped frequency
 cc 
Concept Question
8
6
4
2
0
-2
-4
-6
-8
0
0.5
1
1.5
2
2.5
3
3.
The graph above represents an oscillation that is…
a) Heavily damped b) critically damped
2 - 43
c) lightly da
Concept Question
8
6
4
2
0
-2
-4
-6
-8
0
0.5
1
1.5
2
2.5
3
The period for the oscillation above is approximately…
a) 1.25 seconds
b) 2.5 Hz
c) 0.6 seconds
Estimate the phase shift for the oscillationZero
2 - 44
3.
Forced vibrations can be caused by a test machine, by rocks on a trail, by
rotating machinery, and by earthquakes. Suspension systems, shock
absorbers, and other energy-dissipating devices can help to dampen the
resulting vibrations.
2 - 45
Damped Forced Vibrations
mx  cx  kx  Pm sin  f t
x  xcomplementary  x particular
xm
xm


Pm k 
1
tan  
19 - 46

1  
f
2c cc   f  n

1  f n

2
n 
  2c c 
2 2

c
f
 n 2
 magnification
factor
 phase difference between forcing and steady
state response
Group Problem Solving
SOLUTION:
• Determine the system natural
frequency, damping constant, and
the unbalanced force.
• Determine the steady state
response and the magnitude of the
motion.
A simplified model of a washing machine is shown. A bundle of wet clothes
forms a mass mb of 10 kg in the machine and causes a rotating unbalance.
The rotating mass is 20 kg (including mb) and the radius of the washer
basket e is 25 cm. Knowing the washer has an equivalent spring constant
k = 1000 N/m and damping ratio z = c/cc = 0.05 and during the spin cycle
the drum rotates at 250 rpm, determine the amplitude of the motion.
19 - 47
Group Problem Solving
Given: m= 20 kg, k= 1000 N/m,
f= 250 rpm, e= 25 cm, mb= 10 kg
Find: xm
Calculate the forced circular
frequency and the natural circular
frequency
f 
(2 )(250)
 26.18 rad/s
60
n 
k
1000

 7.0711 rad/s
m
20
Calculate the critical damping constant cc and the damping constant c
cc  2 km  2 (1000)(20)  282.84 N  s/m
19 - 48
c
c
 cc

 c  (0.05)(141.42)  14.1421 N  s/m

Group Problem Solving
Calculate the unbalanced force
caused by the wet clothes
Pm  mb e 2f
Pm  (10 kg)(0.25 m)(26.18 rad/s)2  1713.48 N
Use Eq 19.52 to determine xm
mx  cx  kx  Pm sin  f t
xm 


19 - 49
Pm
k
 m 2f

2
 (c f )2
1713.48
[1000  (20)(26.18)2 ]2  [(141421)(26.18)]2
1713.48
(12,707.8)2  (370.24)2

1713.48
 0.13478 m
12,713.2
xm  134.8 mm
Concept Question
The following parameters were
found in the previous problem:
 f  26.18 rad/s
n  7.0711 rad/s
 =0.05
What would happen to the
amplitude xm if the forcing
frequency f was cut in half?
a) The vibration amplitude remains the
same.
b) The vibration amplitude would
increase.
c) The vibration amplitude would
decrease.
2 - 50
Concept Question
Case 1
 f  26.18 rad/s
n  7.0711 rad/s
Case 2
 f  13.09 rad/s
n  7.0711 rad/s
xm 
2 - 51
Pm

k  m 2f

2
 (c f )2
Electrical Analogues
• Consider an electrical circuit consisting of an inductor,
resistor and capacitor with a source of alternating voltage
Em sin  f t  L
di
q
 Ri   0
dt
C
1
Lq  Rq  q  Em sin  f t
C
• Oscillations of the electrical system are analogous to
damped forced vibrations of a mechanical system.
19 - 52
Electrical Analogues
• The analogy between electrical and mechanical
systems also applies to transient as well as steadystate oscillations.
• With a charge q = q0 on the capacitor, closing the
switch is analogous to releasing the mass of the
mechanical system with no initial velocity at x = x0.
• If the circuit includes a battery with constant voltage
E, closing the switch is analogous to suddenly
applying a force of constant magnitude P to the
mass of the mechanical system.
19 - 53
Electrical Analogues
• The electrical system analogy provides a means of
experimentally determining the characteristics of a given
mechanical system.
• For the mechanical system,
m1x1  c1 x1  c2  x1  x 2   k1 x1  k 2  x1  x2   0
m2 x2  c2  x2  x1   k 2  x2  x1   Pm sin  f t
• For the electrical system,
q q q
L1q1  R1 q1  q 2   1  1 2  0
C1
C2
q2  q1


L2 q2  R2 q 2  q1 
 Em sin  f t
C2
• The governing equations are equivalent. The characteristics
of the vibrations of the mechanical system may be inferred
from the oscillations of the electrical system.
19 - 54
Degree of Freedom (DOF)
• Mathematical modeling of a physical system requires the
selection of a set of variables that describes the behavior
of the system.
• The number of degrees of freedom for a system is the
number of kinematically independent variables necessary
to completely describe the motion of every particle in the
system
DOF=1
DOF=2
Single degree of freedom (SDOF)
Multi degree of freedom (MDOF)
Equivalent model of systems
Example 1:
Example 2:
SDOF
MDOF
DOF=1
DOF=2
Equivalent model of systems
MDOF
Example 3:
DOF= 3 if body 1 has no rotation
SDOF
DOF=2
DOF= 4 if body 1 has rotation
body 1
What are their DOFs?
SDOF systems

Helical springs
Shear stress:
Stiffness coefficient:
F: Force, D: Diameter, G: Shear modulus of the rod,
N: Number of turns, r : Radius

Springs in combinations:
Parallel combination
Series combination
Elastic elements as springs
Moment of Inertia
What are the equivalent stiffnesses?
Example

A 200-kg machine is attached to the end of a cantilever beam of length L=
2.5 m, elastic modulus E= 200x109 N/m2, and cross-sectional moment of
inertia I = 1.8x10–6 m4. Assuming the mass of the beam is small compared to
the mass of the machine, what is the stiffness of the beam?
Damping

Viscous Damping