Download Adjacent angles

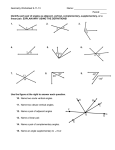
Click the mouse button or press the
Space Bar to display the answers.
Lesson 1-5
Adjacent angles:
are two angles that lie in the same
plane, have a common vertex, and a
common side, but no common
interior points.
Vertical angles:
are two nonadjacent angles formed
by two intersecting lines
Linear pair:
is a pair of adjacent angles whose
noncommon sides are opposite rays.
Name two angles that form a linear pair.
A linear pair is a pair of adjacent
angles whose noncommon sides are
opposite rays.
Answer: The angle pairs that satisfy this definition are
Name two acute vertical angles.
There are four acute
angles shown. There is one pair of
vertical angles.
Answer: The acute vertical angles are VZY and XZW.
Name an angle pair that satisfies each condition.
a. two acute vertical angles
Answer:
BAC and FAE,
CAD and NAF, or
BAD and NAE
b. two adjacent angles whose
sum is less than 90
Answer: BAC and CAD or
EAF and FAN
Complementary angles:
are two angles whose measures have
a sum of 90.
Supplementary angles:
are two angles whose measures have
a sum of 180.
ALGEBRA Find the measures of two supplementary
angles if the measure of one angle is 6 less than five
times the other angle.
Explore
Plan
The problem relates the measures of two
supplementary angles. You know that the sum
of the measures of supplementary angles is 180.
Draw two figures to represent the angles.
Let the measure of one angle be x.
Solve
Given
Simplify.
Add 6 to each side.
Divide each side by 6.
Use the value of x to find each angle measure.
Examine
Add the angle measures to verify that the
angles are supplementary.
Answer: 31, 149
ALGEBRA Find the measures of two complementary
angles if one angle measures six degrees less than
five times the measure of the other.
Answer: 16, 74
Perpendicular lines:
intersect to form four right angles.
Intersect to form congruent
adjacent angles.
Is read is perpendicular to
ALGEBRA Find x so that
.
If
, then mKJH
90. To find x, use KJI and IJH.
Sum of parts
whole
Substitution
Add.
Subtract 6 from each side.
Divide each side by 12.
Answer:
ALGEBRA Find x and y so that
are perpendicular.
Answer:
and
Determine whether the following statement can be assumed from the
figure below. Explain.
mVYT = 90
The diagram is marked to
show that
From the definition of
perpendicular, perpendicular
lines intersect to form
congruent adjacent angles.
Answer:
Yes;
and
are perpendicular.
Determine whether the following statement can be assumed from the
figure below. Explain.
TYW and TYU are supplementary.
Answer:
Yes; they form a
linear pair of angles.
Determine whether the following statement can be assumed from the
figure below. Explain.
VYW and TYS are adjacent angles.
Answer:
No; they do not
share a common side.
Determine whether each statement can be assumed
from the figure below. Explain.
Answer:
Yes; lines TY and SX
a.
are perpendicular.
b. TAU and UAY are
complementary.
c. UAX and UXA are adjacent.
Answer:
No; the sum of the
two angles is 180, not 90.
Answer:
No; they do not share
a common side.
Homework:
Lesson 1-5, p. 41
# 8-22,
24-34 even,
41, 43