* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Tree diagrams and the binomial distribution
Survey
Document related concepts
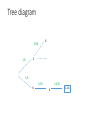
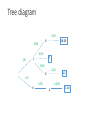
Transcript
Tree diagrams and the binomial distribution Outline for today Better know a player: Dock Ellis Questions about worksheet 6? Review of concepts in probability: additive and multiplicative rules Tree diagrams and the analysis of Strat-o-matic The binomial distribution Announcement: class final projects Start thinking about your class final project Ideally focus on research question • Doesn’t have to be about baseball, but need to find data set that you can use to answer the question 1-2 paragraph proposal is due the Wednesday after spring break (March 23rd) Projects presentation are on April 25st Better know a player: Dock Ellis Probability Probability is a way of measuring the uncertainty of the outcome of an event Definitions: Sample space • All possible outcomes An Event • Subset of the sample space Probability key properties: • 0 ≤ Pr(X) ≤ 1 • Σ Pr(X = x) = 1 Probability rules - Additive rule If there are two events A, and B, then the probability of A or B happening is: Pr(A or B) = Pr(A) + Pr(B) – Pr(A, B) Events are called mutually exclusive if events A and B can not both occur - i.e., Pr(A, B) = 0 Q: What would mutually exclusive events look like in the Venn diagram? A: The circles would not overlap Multiplicative Rule Pr(A, B) = Pr(A|B) × Pr(B) Probability of B happening × Probability of A happening given B happened Two events are independent if: Pr(A, B) = Pr(A) x Pr(B) i.e., if the occurrence of B does not effect the probability of A happening Lottery problem Question 4c: Suppose there was a lottery where you needed to select 5 numbers from 1 to 69 but the order of the numbers mattered • E.g., (2, 4, 6, 8, 10) different entry than (4, 2, 6, 8, 10) What would the probability of winning this lottery be? 1/69 · 1/68 · 1/67 · 1/66 · 1/65 = 7.1 · 10-10 Big League Baseball For any one pitch (not assuming that the play is in play), what is the probability of a the following events? • • • • A home run? A out? A single? A Hit? 1/36 · 1/3 24/36 · 1/3 7/36 · 1/3 10/36 · 1/3 1st Die 2nd Die 1 2 3 4 5 6 1 Single Out Out Out Out Error 2 Out Double Single Out Single Out 3 Out Single Triple Out Out Out 4 Out Out Out Out Out Out 5 Out Single Out Out Out Single 6 Error Out Out Out Single Home run Strat-o-matic Much more complex board games • Takes into account Hitters and Pitchers • Advanced version accounts for additional factors (e.g., ball parks etc.) Strat-o-matic rules and tree diagrams Each player is represented by a card 1. A white single die is rolled to determine whether to use hitter or pitcher’s card: • 1-3 -> hitters card • 4-6 -> pitcher’s card 2. Then, two dice are rolled and their sum determines which play in the card should be used 3. For some plays additionally a 20 sided die is rolled to determine the final outcome • and other tables/rules often need to be consulted Strat-o-matic: analysis Let’s calculate the probability of different events… Calculating the probability of getting a particular column pitcher or hitter’s card is pretty simple • Answer? Calculating the sum of the two dice is a little more involved… • What is the sample space here? • i.e., how many possible outcomes are there? • Can you calculate the probability distribution? Strat-o-matic: analysis Fill in the table below with the sum of the two dice and then calculate the probability of rolling a 2 to a 12 2nd Die 1st Die 1 1 2 3 4 5 6 2 3 7 4 5 6 Strat-o-matic: analysis Fill in the table below with the sum of the two dice and then calculate the probability of rolling a 2 to a 12 1st Die 2nd Die 1 2 3 4 5 6 1 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5 6 7 8 9 10 5 6 7 8 9 10 11 6 7 8 9 10 11 12 Strat-o-matic: analysis 2 1/36 3 2/36 4 3/36 5 4/36 6 5/36 7 6/36 8 5/36 9 4/36 10 3/36 11 2/36 1st Die 2nd Die 1 2 3 4 5 6 1 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5 6 7 8 9 10 5 6 7 8 9 10 11 6 7 8 9 10 11 12 12 1/36 Strat-o-matic: analysis 2 1/36 3 2/36 4 3/36 5 4/36 6 5/36 7 6/36 8 5/36 9 4/36 10 3/36 11 2/36 12 1/36 What is the probability of rolling a 1 on the white die and then getting a sum of 7 on the two red dice? • 1/6 · 6/36 = 6/216 What is the probability of rolling a 2 on the white die and then getting a sum of 8 on the two red dice, and then a number for 1-8 on the 20 sided die? • 1/6 · 5/36 · 8/20 = .00926 Strat-o-matic: analysis 2 1/36 3 2/36 4 3/36 5 4/36 6 5/36 7 6/36 8 5/36 9 4/36 10 3/36 11 2/36 12 1/36 What is the probability of rolling a 1 on the white die or a 6 on the white die? • 1/6 + 1/6 = 2/6 What is the probability of rolling a 5 on the white die and then getting a sum of 8 or a sum of 10 on the two red dice? • 1/6 · (4/36 + 3/36)= .0324 Strat-o-matic: analysis 2 1/36 3 2/36 4 3/36 5 4/36 6 5/36 7 6/36 8 5/36 9 4/36 10 3/36 11 2/36 12 1/36 What is the probability of rolling a 3 on the white die • and then getting a sum of 8 two red dice • or a sum of 10 on the two red dice • and then a 1-10 on the 20 sided die? Tree diagram! 5/36 8 1/6 · 5/36 = .0231 .0231 + .0069 = .0300 1/6 3 10 3/36 1-10 10/20 1/6 · 3/36 · ½ = .0069 Strat-o-matic: Pujols vs. Kershaw What is the probability of a hitting a double? Strat-o-matic: Pujols vs. Kershaw What is the probability of a hitting a double? Strat-o-matic: Pujols vs. Kershaw 2 1/36 3 2/36 4 3/36 5 4/36 6 5/36 7 6/36 8 5/36 9 4/36 10 3/36 11 2/36 12 1/36 Tree diagram 6 5/36 1/6 1 1/6 6 14/20 5/36 6 1-14 Tree diagram 3/20 6 5/36 18-28 6/36 1/6 7 1 5/36 2/20 8 1-2 1/6 6 14/20 5/36 6 1-14 Strat-o-matic: Pujols vs. Kershaw What is the probability of a hitting a double? Tree diagram! 1/6 · [5/36 · 3/20 + 6/36 + 5/36 · 2/20] + 1/6 · (5/36 14/20) = .04977 Strat-o-matic: Pujols vs. Kershaw What is the probability of a hitting a home run? Strat-o-matic: Pujols vs. Kershaw What is the probability of a hitting a home run? Tree diagram! 1/6 · [3/36 + 4/36 + 5/36 · 17/20] + 1/6 · (4/36 · 2/20) = .0594 Back to the lottery problem Question 4c: Suppose there was a lottery where you needed to select 5 numbers from 1 to 69 but the order of the numbers mattered • E.g., (2, 4, 6, 8, 10) different entry than (4, 2, 6, 8, 10) What would the probability of winning this lottery be? 1/69 · 1/68 · 1/67 · 1/66 · 1/65 = 7.1 · 10-10 Lottery problem Question 4d: Suppose there was a lottery where you needed to select 5 numbers from 1 to 69 and the order of the numbers does not mattered • E.g., (2, 4, 6, 8, 10) is the same as (4, 2, 6, 8, 10) Solution: we need to count how many permutations there are of 5 numbers, and then use the additive rule to add all these together • i.e., multiply 7.1 · 10-10 by the number of permutations Q: How many permutations are there? Lottery problem A slightly easier problem: suppose there were 5 letters and we needed to find all the ways to select 2 letters • i.e., we have A, B, C, D, E to put into two slots There would be 5 letter choices for the 1st slot And there would be 4 letter choices for the 2nd slot A B C D E B C D E A 1 2 5 · 4 = 20 ways to permute 2 out of 5 objects Let’s write out these 20 permutations! Lottery problem Continuing this process there would be 3 letters to choose for the second slot 5 · 4 · 3 = 60 ways to permute 3 out of 5 objects Continuing this pattern we get: 5 · 4 · 3 · 2 · 1 = 120 ways to permute 5 out of 5 objects B C D E B C D E A C 1 2 B D E 3 i.e., we have factorial 5! Lottery problem Question 4d: Suppose there was a lottery where you needed to select 5 numbers from 1 to 69 and the order of the numbers does not mattered • E.g., (2, 4, 6, 8, 10) is the same as (4, 2, 6, 8, 10) Solution: we need to use the additive rules to count how many permutations there are of 5 numbers and then use the additive rule to add all these together • i.e., multiply 7.1 · 10-10 by the number of permutations A: 120 · 7.1 · 10-10 = 8.9 · 10-8 http://www.webmath.com/lottery.html n choose k We can write this as • Pr(winning lottery) = 120 · (1/69 · 1/68 · 1/67 · 1/66 · 1/65) • Or 1 in (69 · 68 · 67 · 66 · 65)/120 chance of winning More generally let’s say were are choosing k items out of n total • n = 69 • k=5 We can then calculate this using the “n choose k” function n choose k Q: How many ways are there to choose 3 things out of a total of 10? A: (10 · 9 · 8)/ (3 · 2) = 120 R: choose(n, k)