Download 15-2: Trapezoids Objectives: To discover and use properties of

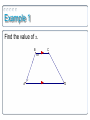
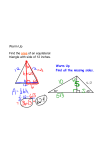
15-2: Trapezoids
Objectives:
1. To discover and use
properties of
trapezoids
2. To find the area of
trapezoids
Assignment:
SpringBoard:
• P: 212: 11, 12
• P. 221: 2-4
Purple Geometry Text:
• P. 546-9: 6-9, 32, 37-39
• P.733-6: 5, 16, 17, 19, 26,
29
• Almost a Trapezoid
Worksheet
You will be able to
discover and use
properties of trapezoids
Objective 1
Trapezoids
What makes a quadrilateral a trapezoid?
Trapezoids
A trapezoid is
a quadrilateral
with exactly
one pair of
parallel
opposite sides.
Trapezoid Parts
The parallel sides are
called bases
The non-parallel
sides are called legs
A trapezoid has two
pairs of base angles
Example 1
Find the value of x.
C
B
100
x
A
D
Trapezoid Theorem 1
If a quadrilateral is a trapezoid, then the
consecutive angles between the bases are
supplementary.
C
B
y
x
A
t
r
D
If ABCD is a trapezoid, then x + y = 180° and r + t = 180°.
Midsegment
A midsegment of a
trapezoid is a
segment that
connects the
midpoints of the
legs of a
trapezoids.
Investigation 1
In this Investigation, you
will be using
Geometer’s Sketchpad
to construct an
isosceles trapezoid,
and then you will
discover some
properties about its
base angles, diagonals,
and midsegment.
Trapezoid Midsegment Theorem
The midsegment of a
trapezoid is parallel
to each base and its
length is one half
the sum of the
lengths of the
bases.
If
Example 2
Find the value of x.
Example 3
Given: Trapezoid 𝐸𝐹𝐺𝐻
𝑀𝑁 is a midsegment
Prove: 𝑀𝑁 ∥ 𝐹𝐺 and 𝑀𝑁 ∥ 𝐸𝐻
𝑀𝑁 =
1
2
𝐹𝐺 + 𝐸𝐻
Isosceles Trapezoid
An isosceles trapezoid is a
trapezoid with congruent legs.
Trapezoid Theorem 2
If a trapezoid is isosceles, then each pair of
base angles is congruent.
Trapezoid Theorem 3
A trapezoid is isosceles if and only if its
diagonals are congruent.
T
i
Example 4
Find the measure of each missing angle.
Example 5
Given: Trapezoid 𝐶𝑂𝑅𝐸
𝐶𝑂 ≅ 𝐸𝑅
Prove: 𝐶𝑅 ≅ 𝐸𝑂
Objective 2
You will be able to find the area of trapezoids
Investigation 2
Now you will discover
a justification for
the area formula for
trapezoids.
Trapezoid Area
Example 6
Find the area of the polygon.
Example 7
Find the area of the trapezoid.
15-2: Trapezoids
Objectives:
1. To discover and use
properties of
trapezoids
2. To find the area of
trapezoids
Assignment:
SpringBoard:
• P: 212: 11, 12
• P. 221: 2-4
Purple Geometry Text:
• P. 546-9: 6-9, 32, 37-39
• P.733-6: 5, 16, 17, 19, 26,
29
• Almost a Trapezoid
Worksheet