Download Unit 5 - mszhu

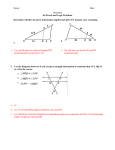
What was your goal?
 What was your actual grade?
 Why did you meet/not meet your goal?
 What were your strengths?
 What areas do you need to work on?
 What are you going to do to succeed on
the next test?

Angles of a Triangle

Write down everything you remember
about triangles!

By Side:
› Equilateral—all sides congruent
› Isosceles—two sides congruent
› Scalene—no sides congruent

By Angle:
› Obtuse—one angle greater than 90°
› Right—one angle equal to 90°
› Acute—all angles less than 90°
Interior Angles add up to 180°
 Exterior Angles add up to 360°
 Examples:
› In triangle DEF; ∠D = 45°, ∠E = 30°. Find ∠F.

› In triangle ABC; ∠C = 3x – 5, ∠B = x + 40
and ∠A = 2x + 25. Find the measures of all
three angles.
2x + 5
3x – 5
x + 40
CPCTC and SSS

Congruent line segments are marked with
a small dash

Congruent angles are marked with an arc

Parallel lines are marked with arrows

To separate different pairs of congruent
line segments or angles, we use different
numbers of dashes or arcs



Corresponding = matching
Order of the letters matters!
Example: ΔABC = ΔDEF. Which angles are
congruent? Which sides are congruent?


SSS Postulate: If all three corresponding
sides of two triangles are congruent,
then the triangles are congruent
Example: ΔFEG = ΔKJL because of SSS.
SAS, ASA, AAS, HL

Name all the corresponding angles if
ΔIJH ≅ ΔKJL.
∠SRU ≅ ∠STU
 ∠RSU ≅ ∠TSU
 ∠RUS ≅ ∠TUS

Yes, can be proven through SSS



∠BRD ≅ ∠DYB
∠RBD ≅ ∠YDB
∠RDB ≅ ∠YBD



BR ≅ DY
BY ≅ DR
BD ≅ BD

Side-Side-Side (SSS)

Side-Angle-Side (SAS)
› Sandwich!

Angle-Side-Angle (ASA)
› Sandwich!

Angle-Angle-Side (AAS)
› No sandwich!

Hypotenuse-Leg (HL)
› Right triangles only!
Identity Properties in
Triangle Proofs

Reflexive Property: AB ≅ AB (congruent to itself)

Transitive Property: AB ≅ BC, BC ≅ CD, so AB ≅ CD

Additive Property: Adding the same amount to two
congruent parts results in two equal sums

Multiplicative Property: Multiplying two congruent
parts by the same number results in two equal
products
1.
2.
3.
4.
5.
Mark diagram with “Given” and write as Step 1.
Figure out how many parts of the triangles you
know are congruent, and how many you need to
prove congruent.
Mark missing congruent parts on diagram, using
info from theorems you know (vertical angles,
etc.). Write these down in the two columns.
Prove triangles congruent using: SSS, SAS, ASA,
AAS, or HL.
Check: Make sure you used all info in the “Given.”
Make sure your last step matches the “Prove”.


Given: GJ ≅ JI
HJ ┴ GI
Prove: ΔGJH ≅ ΔIJH
Statement
Reason
1. GJ ≅ JI
HJ ┴ GI
1. Given
2. ∠GJH ≅ ∠IJH
2. ┴ lines form right angles, all
right angles are ≅
3. HJ ≅ HJ
3. Reflexive property
4. ΔGJH ≅ ΔIJH
4. SAS
Line/Angle Theorems in
Triangle Proofs

Midpoint
› Halfway point on a line
segment

Bisect
V is the midpoint of TW
› Split a line segment or angle into two equal
parts
HJ bisects GI

Vertical Angles
› ALWAYS congruent; (“X”)

Alternate Interior Angles
› ONLY congruent when we know lines are
parallel (“Z”)
› ABCD is a
parallelogram
1.
2.
3.
4.
5.
Mark diagram with “Given” and write as Step 1.
Figure out how many parts of the triangles you
know are congruent, and how many you need to
prove congruent.
Mark missing congruent parts on diagram, using
info from theorems you know (vertical angles,
etc.). Write these down in the two columns.
Prove triangles congruent using: SSS, SAS, ASA,
AAS, or HL.
Check: Make sure you used all info in the “Given.”
Make sure your last step matches the “Prove”.


Given: HK bisects IL
∠IHJ ≅ ∠JKL.
Prove: ΔIHJ ≅ ΔLKJ
Statement
Reason
1. HK bisects IL
∠IHJ = ∠JKL
1. Given
2. IJ ≅ JL
2. Definition of “bisect”
3. ∠IJH ≅ ∠LJK
3. Vertical angles congruent
4. ΔIHJ ≅ ΔLKJ
4. AAS
Using Quadrilateral
Theorems in Triangle
Proofs

Parallelogram
Rhombus
Rectangle
Square

ALSO WATCH OUT FOR:



›
›
Alternate Interior Angles
Vertical Angles
•
•
•
Opposite sides are parallel
and congruent
• AB  CD, AD  CB
• AB CD, AD CB
Opposite angles are
congruent
• DAB  BCD, ABC  CDA
Diagonals bisect each other
• Bisect = to split in half
•
Has all the properties of a
parallelogram, plus:
• FOUR congruent sides
• Diagonals are
perpendicular and
bisect
•
Has all properties of a
parallelogram, plus:
• Four right angles
• Congruent
diagonals that
bisect
•
•
Four congruent sides
and four right angles
Diagonals are
congruent and
perpendicular; also
bisect


Given: FLSH is a parallelogram;
LG ┴ FS, AH ┴ FS
Prove: ΔLGS ≅ ΔHAF
Statement
Reason
1. FLSH is a parallelogram;
LG ┴ FS, AH ┴ FS
1. Given
2. LG ≅ FH
2. Opp. sides of p.gram are ≅
3. ∠LGS ≅ ∠HAF
3. ┴ lines form right ∠’s, all
right ∠’s ≅
4. ∠LSG ≅ ∠HFA
4. Alt. int. ∠’s ≅ when lines ||
5. ΔLGS ≅ ΔHAF
5. AAS
Using Circle Theorems in
Triangle Proofs

Chords intercepting congruent arcs are congruent

Tangent is perpendicular to
the radius at the point where it
touches the circle

Arcs between parallel lines are
congruent
J
H
G
F

Inscribed angle is half the
intercepted arc.
N

Two inscribed angles that
intercept the same arc
are congruent
J
L
M
Given: arc BR = 70°, arc YD = 70°;
BD is the diameter of circle O
 Prove: ΔRBD ≅ ΔYDB

Statement
Reason
1. Arc BR = 70°, arc YD = 70°;
BD is the diam. of circle O
1. Given
2. BD ≅ BD
2. Reflexive
3. ∠YBD = 35°, ∠RDB = 35°
3. Inscribed angles = ½ arc
4. ∠YBD ≅ ∠RDB
4. ≅ arcs have same measure
5. ∠BYD ≅ ∠BRD
5. Inscribed angles intercepting
same arc are ≅
5. ΔRBD ≅ ΔYDB
6. AAS