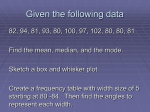
Download Session 1: Statistical Variation and the Normal Curve

Chapter 1: Statistical Variation and the Normal Curve
1.0
Introduction
Perhaps the most striking feature of observation or real data values from almost any
discipline is the variation they exhibit. If a nurse measures physical dimensions
(heights, weights..) or blood parameters (Serum albumin or cholesterol..) for a sample of
patients, they will (nearly) all be different. If a educational psychologist administers a
psychological test to a sample of children or if impairment is measured using a response
time test, the tests scores in each case will vary greatly. Indeed a manufacturing
engineer who measures the physical dimensions (e.g., outer diameter or length) of
components manufactured to the same specifications will find they exhibit precisely the
same type of variation as the psychological test scores. Similarly, a cosmetic scientist
who measures the depth of wrinkles on women’s faces, or environmental scientists
measuring acidity levels (pH values) in samples from different lakes or streams, or from
one site sampled at different times, or indeed if they measure birds’ eggs, they will find
very much the same kind of variation as did the engineer, psychologist or nurse referred
to above.
This variation is the reason why statistical methods are used across a wide range of
disciplines. Statistics is the science of describing and analysing chance variation, and
statistical methods help us describe the nature of chance or random variation and ‘tame’
it.
This chapter is concerned with describing such variation using:




1.1
Pictures
Normal or Gaussian curve
Additive variation and averages – the implications of adding chance quantities
(central to this course)
Measurement systems and control charts.
Statistical Variation
We begin with a series of examples to illustrate statistical variation in a number of
disciplines. The histogram in Figure 1.1.1 is based on a dataset (Grades) that comes
with the Minitab software [1] that will be used extensively in this course manual.
Investigators in the USA collected data to investigate the relationship between SAT
scores (Scholastic Aptitude Test, often used as a college admission or course placement
Course Manual: PG Certificate in Statistics, TCD, Base Module
1
criterion) and GPA grades (grade point average – university performance score). Figure
1.1.1 gives the Verbal SAT scores of 200 students. This picture is typical of what we
might expect from psychological/educational test results – the students cluster around
the central value (about 600, here) and the number of students who get scores far from
the centre is quite small – the numbers decrease in a more or less symmetrical manner
in each direction.
300
400
500
600
700
800
Figure 1.1.1: SAT Verbal scores for 200 university students
The histogram in Figure 1.1.2 shows the distribution of capping torques (in lbs-inches)
of 78 container caps; the capping torque is a measure of the energy expended in
breaking the seal of the screw-capped containers. The data come from a process
capability study of a newly installed filling line in a company that manufactures
chemical reagents. It is interesting to note that the physical measurements display
similar characteristics to the psychological scores – they vary in a roughly symmetrical
way around a central value (about 10.8 for the torques).
7.5
8.5
9.5
10.5
11.5
12.5
13.5
Figure 1.1.2: Capping torques (lb-in) for 78 screw-capped containers
Course Manual: PG Certificate in Statistics, TCD, Base Module
2
Figure 1.1.3 shows a histogram of the distribution of petal lengths of a sample 50 irises
from the variety Setosa. The data were originally published in the Bulletin of the
American Iris Society [2], but their frequent citation in the statistical literature is due
to their use in the pioneering paper on multivariate analysis by R.A. Fisher [3]. This
botanical/environmental science example exhibits the same symmetry characteristics
noted above for the psychological and industrial data.
1.0
1.2
1.4
1.6
1.8
Figure 1.1.3: Petal lengths (mm) for 50 irises (Setosa)
In Figure 1.1.4 the histogram displays the distribution of the heights (cm) of pregnant
women (website of Prof. Martin Bland a well-known medical statistician, [4]). Because
the sample size is so large (1794 values) the histogram is much smoother and the
symmetry is much better defined, than for the smaller sample sizes of the first three
examples. In Section 1.3 we will see that all four datasets are consistent with
underlying Normal or Gaussian distributions - smooth symmetrical bell-shaped curves
(see Figure 1.1.6) that will be discussed in some detail in Section 1.2. Consequently,
any departures from symmetry in our histograms are considered due to the variability
necessarily associated with relatively small sample sizes.
Importantly observe that both the women’s heights and petal lengths data have many
repeated values, this occurs due to rounding of a lack of precision in the measurement
systems. For data values arising from the mathematical (i.e. idealised) Normal
Distribution this typically does not occur.
Course Manual: PG Certificate in Statistics, TCD, Base Module
3
144
152
160
168
176
184
Figure 1.1.4: Heights (cm) of 1794 pregnant women
While this symmetrical shape is very common, it is by no means universal, as
illustrated by our next example.
Figure 1.1.5.
-OHCS) values in nmol/24h “obtained on a random sample of
100 obese adult females drawn from a fully specified target population”; the data come
from the book on laboratory medicine by Strike [5]. The steroid data show a long tail on
the right, in other words they are strongly skewed (to the right); the characteristic
described by the graph is very different from those of our first four examples. Most of
the steroid measurements are less than 900 but individual values range up to around
1400. While it is now possible to deal directly with skewed data, traditionally, analysts
sought transformations which would allow the data to be analysed using methods based
on the Normal distribution; this is still a common practice.
200
400
600
800
1000
1200
1400
Figure 1.1.5: Urinary β-hydroxycorticosteroid (nmol/24h) values for 100 obese
females
Course Manual: PG Certificate in Statistics, TCD, Base Module
4
Figure 1.1.6 shows a histogram (with a superimposed Normal curve) of the transformed
data after the original measurements were subjected to transformation by taking
logarithms (to base 10). As we shall see in Section 1.3 the transformation has been
successful – the transformed data are well modelled by a Normal curve. Where
transformed data follow a Normal curve, the original skewed distribution is said to be
‘log-Normal’.
2.4
2.6
2.8
3.0
3.2
Figure 1.1.6: Transformed (logarithms) steroid data
There are of course very many different types of shape that may be encountered for
histograms of real data (more will be presented during the lectures). However, Figures
1.1.1-1.1.6 were selected for presentation, both to illustrate the wide applicability of the
Normal curve (in terms of discipline type) and the possibility of transforming data so
that they follow this curve, which is, perhaps, the easiest of all statistical distributions
to use – hence its popularity. It is also of fundamental importance because averages of
data sampled from skewed distributions will, in many cases, follow a Normal curve (see
Section 1.5) – this means that methods developed for Normal data can be applied to
such averages, even though the underlying data are skewed.
Aside: Many important distributions are skewed to the right including the income distribution
and the distribution of city sizes (Zift’s law) – these are example a very important applied
distribution known as the Pareto Distribution; search Wikipedia for details of these distributions
and for example the famous 80-20 Rule derived from the Pareto Distribution.
Note: The fact that a distribution is skewed does not mean that statistical analysis fails, in
particular analysis of the means of many differing samples taken from any one of these
distributions yields to the type of straightforward statistical analysis covered in this course.
Course Manual: PG Certificate in Statistics, TCD, Base Module
5
1.2 The Normal (Gaussian) curve
If the more or less symmetrical histograms of Sections 1.1 were based on several
thousand observations, the bars of the histograms could be made very narrow and the
overall shapes might then be expected to approximate the smooth curve shown below as
Figure 1.2.1.
Figure 1.2.1: The Normal curve
This is a mathematical curve described using two parameters, the mean μ and standard
deviation σ. It is symmetric about its centre, the mean, and its width is measured by the
standard deviation. The standard deviation is formally defined but can usefully be
thought of as one sixth of the width of the curve, for most practical purposes. In
principle, the curve stretches from minus infinity to plus infinity but in practice (as can
be seen from Figure 1.2.1) the area in the tails becomes infinitesimally small very
quickly.
Interpreting the Normal Curve
Figure 1.2.2 shows three Normal curves with the mean μ and standard deviation σ. The
curves are drawn so that the total area enclosed by each curve is one; when this is done
we call the Normal Curve the Normal (Gaussian) Distribution. Then, approximately
68% of the area lies within 1 standard deviation of the mean; the corresponding values
for two and three standard deviations are 95% and 99.7%, respectively. These areas
will be the same for all Normal curves irrespective of the values of the means and
standard deviations.
Course Manual: PG Certificate in Statistics, TCD, Base Module
6
Figure 1.2.2: Areas within one, two and three standard deviations of the
mean
The implications of this figure are that if the variation between measurements on
individuals/objects (e.g. blood pressure, SAT scores, torques, etc.) can be described by a
Normal curve, then 68% of all values will lie within one standard deviation of the mean,
95% within two, and 99.7% within three standard deviations of the mean. Similarly, if
we have a measurement error distribution that follows a Normal curve, then in 32% of
cases the chance error will result in a measured value being more than one standard
deviation above or below the mean (the ‘true value’ if the measurement system is
unbiased). In only 5% (or 1-in-20) of cases will the observation be further than two
standard deviations from the mean.
Figure 1.2.3: Distribution of the masses of filled containers
Suppose that the Normal curve shown in Figure 1.2.3 represents the masses of filled
containers sampled from a filling line. The curve is interpreted as an idealised
histogram for which the total area (or probability) is 1.0. The area between any two
points (say x1 and x2) represents the relative frequency (probability) of container
masses between x1 and x2. If this area is 0.2 it means that 20% of all containers filled
by this line have masses between x1 and x2 units. The assumption is that, provided the
Course Manual: PG Certificate in Statistics, TCD, Base Module
7
filling process remains stable, 20% of all future fillings will result in containers with
masses between x1 and x2 units. Since relative frequencies are generally of interest,
e.g. what fraction of values is less than or greater than a given value, or what fraction
lies between two given values, then, where a Normal curve describes the variability in
question, it can be used to calculate the required relative frequency. Note the area to the
left of x1 is the probability that any observation x selected from this distribution at
random will be less than x1, this is formally written as
𝑃(𝑥 < 𝑥1 )
The use of probability as a way of expressing uncertainty has become common in
everyday speech. Our concept of probability is intimately bound up with the idea of
relative frequency and people move easily between the two ways of describing
variability. Thus, it seems quite natural to say that if a filled container is selected at
random, the probability is 0.2 that its mass will lie between x1 and x2. We typically
write this as
𝑃(𝑥1 < 𝑥 < 𝑥2 ) = 0.2
Both of these ways of describing variability, viz., relative frequency and probability, are
equivalent, and they will be used interchangeably hereafter.
Obtaining Areas under Normal Curves
Figure 1.2.4: A standard Normal curve (z) and an arbitrary Normal curve
(x)
Course Manual: PG Certificate in Statistics, TCD, Base Module
8
All Normal curves have essentially the same shape once allowance is made for different
standard deviations. This allows for easy calculation of areas, i.e., relative frequencies
or probabilities. If, for any arbitrary curve with mean µ and standard deviation σ, the
area between two values, say x1 and x2, is required, all that is necessary is to find the
corresponding values z1 and z2 on the standard Normal curve, determine the area
between z1 and z2 and this will also be the area between x1 and x2 (as shown
(schematically) in Figure 1.2.4). A standard Normal curve has mean zero and standard
deviation one.
Standard Normal μ=0, σ=1
The z value is the answer to the question “by how many standard deviations does x
differ from the mean μ?”
Once the z value is calculated, the area to its left (i.e. the area from minus infinity up to
this value of z) can be read from a standard Normal table (Table ST-1), this is formally
written as
𝑃(𝑧 < 𝑧1 ).
Thus, a z value of 2 has an area to its left of 0.9772, or
𝑃(𝑧 < 2) = 0.9772.
while a z value of 1.5 has an area to its left of 0.9332, or
𝑃(𝑧 < 1.5) = 0.9332.
Therefore, the area or probability between z=1.5 and z=2 on the standard Normal curve
is 0.9772 - 0.9332 or 0.0440, or
𝑃(𝑧1 < 𝑧 < 𝑧2 ) = 0.9772 − 0.9332 = 0.0440.
Similarly, the area between two points which are 1.5 and 2 standard deviations from
the mean of any Normal curve will also be 0.0440.
The relationship or transformation formula between the x and z values is simple:
z
x

.
And the inverse relationship is
𝑥 = 𝜇 + 𝜎𝑧
Course Manual: PG Certificate in Statistics, TCD, Base Module
9
Example 1
Figure 1.1.4 showed a distribution of heights for a population of women. The mean of
the 1794 values was 162.4 and the standard deviation was 6.284. If we take the mean
and standard deviation as those of the corresponding population, we can address
questions such as those below.
(i)
(i)
What fraction of the population has a height greater than 170 cm?
(ii)
What fraction of the population has a height less than 145 cm?
(iii)
How tall would I be if I was taller than 75% of the population??
(iv)
What bounds should we use if we want to enclose the central 95% of the
population within them?
What fraction of the population has a height greater than 170 cm?
To calculate the required proportion of the population, the area to the right of 170 on
the height curve must be found. So we require
𝑃(𝑥 > 170)
Figure 1.2.5: The standard Normal curve (z) and the women’s heights curve (x)
Looking at Figure 1.2.5 we see on the right the Normal Curve for the observed values
centred at μ=164.2. To get the equivalent value on the Standard Normal scale (Normal
curve on the left) we apply the formula to go from (x) values to (z) values. So the
transformation from the height (x) to the standard Normal scale (z) is given by:
z
x

Course Manual: PG Certificate in Statistics, TCD, Base Module

170  162.5
 1.21
6.284
10
Thus, a height of 170 corresponds to the point 1.21 on the standard Normal scale. The
Standard Normal tables give the area to the left of z = 1.21 as
𝑃(𝑧 < 1.21) = 0.8869.
But, the sign is > so we want the area on right, i.e.
𝑃(𝑥 > 170) = 𝑃(𝑧 > 1.21)
Importantly, since the total area is 1, the area to the right is
Area to the right = 1 − 𝐴𝑟𝑒𝑎 𝑡𝑜 𝐿𝑒𝑓𝑡
We formally write this as
𝑃(𝑧 > 1.21) = 1 − 𝑃(𝑧 < 1.21) = 1 − 0.8869 = 0.1131.
Accordingly, approximately 11% of the women will have a height greater than 170 cm.
The calculations are usually summarised in one expression as follows:
𝑃(𝑥 > 170 = 𝑃 (𝑧 >
170 − 164.2
) = 𝑃(𝑧 > 1.21) = 1 − 𝑃(𝑧 < 1.21) = 1 − 0.8869 = 0.1131.
6.284
We can read P(x >170) as “the proportion of x values greater than 170” or, equivalently,
as “the probability that a single x value, selected at random, will be greater than 170”.
(ii)
What fraction of the population has a height less than 145 cm?
The value of z that corresponds to 145 is given by:
z =
x

 145  162.4 = –2.77.
6.284
Statistical Table-1 (ST-1) only gives areas for positive values of z. However, we can use
the symmetry of the curve to find areas corresponding to negative values. Thus,
P(z<2.77) is the area below 2.77; 1–P(z<2.77) is the area above +2.77. By symmetry this
is also the area below –2.77, as shown in Figure 1.2.6
Course Manual: PG Certificate in Statistics, TCD, Base Module
11
-2.77
0
2.77
Figure 1.2.6: The symmetry property of the Normal curve (area is 0.0028 in each tail)
Accordingly, we have:
P(X < 145) =P(z < –2.77) = P(z >2.77) = 1 – P(z < 2.77) = 1 – 0.9972 = 0.0028.
Approximately 0.3% will have heights less than 145 cm.
(iii) How tall would I be if I was taller than 75% of the population?
In this case 75% of the population are smaller than I am. So, the area to the left on the
Standard Normal is 0.75, or
𝑃(𝑧 < 𝑧1 ) = 0.75.
1
0.8
0.6
0.4
0.2
0.75
-2.5
-2.2
-1.9
-1.6
-1.3
-1.0
-0.7
-0.4
-0.1
0.2
0.5
0.8
1.1
1.4
1.7
2.0
2.3
0
Course Manual: PG Certificate in Statistics, TCD, Base Module
12
So, what is the z-value corresponding to this probability on the Standard Normal. To get
this read the tables is reverse; in other words find the cell value in the body of the table
that is closest to 0.75 and read the associated cell value from the left most column and
top row (add these values), we get
𝑃(𝑧 < 𝑧1 ) = 0.75 => 𝑧1 = 0.675 .
To convert this back to height (x) scale apply the inverse transformation
𝑥 = 𝜇 + 𝜎𝑧 = 162.4 + 6.284 × 0.675 = 166.6
Thus, if I was 167 cm’s I would be taller than 75% of the women in the population.
(iv)
What bounds (A, B) should we use if we want to enclose the central 95% of the
population within them?
Figure 1.2.7: Finding the central 95% limits
To find the values that enclose the central 95% of the standard Normal curve (i.e., an
area of 0.95) we proceed as follows. Enclosing the central 0.95 means we leave 0.025 in
each tail. The upper bound, therefore, has an area of 0.975 below it (as shown in the
leftmost curve in Figure 1.2.7). If we inspect the body of Table ST-1, we find that 0.975
corresponds to a z value of 1.96. By symmetry, the lower bound is –1.96 (the central
curve in Figure 1.2.7). Thus, a standard Normal curve has 95 % of its area between z=–
1.96 and z=+1.96. From the relation:
z
x

Course Manual: PG Certificate in Statistics, TCD, Base Module
13
Using the reverse transformation we get:
1.96 
B

=>
B = μ + 1.96 σ
=>
A = μ – 1.96 σ
and:
– 1.96 
A 

It is clear, then, that the values that enclose the central 95% interval of the population
for an arbitrary Normal curve (x) with mean μ and standard deviation σ are: μ - 1.96 σ
and μ + 1.96 σ; this is generally called the 2 standard deviation interval about the mean
and it is ubiquitous throughout statistical practice in many disciplines -.
In the present case this gives us: 162.4±1.96(6.284), i.e., 162.4±12.3. While this gives
(150.1, 174.7), for practical purposes the bounds would probably be described as 150 to
175 cm.
Example 2
Suppose the distribution of capping torques for a certain product container is Normal
with mean μ=10.6 lb-in and standard deviation σ=1.4 lb-in (these were the values
obtained from the data on which Figure 1.1.2 is based). To protect against leaks, a
minimum value for the torque must be achieved in the manufacturing process. If the
lower specification limit on torque is set at 7 lb-in, what percentage of capping torques
will be outside the lower specification limit?
To calculate the required percentage, the area to the left of 7 on the capping process
curve must be found. To do this, the equivalent value on the standard Normal curve is
calculated; the area to the left of this can be found easily and this gives the required
proportion (as illustrated schematically in Figure 1.2.8).
Figure 1.2.8: The standard Normal curve and the capping process curve
Course Manual: PG Certificate in Statistics, TCD, Base Module
14
The translation from the torque scale (x) to the standard Normal scale (z) is given by:
z
x

z = 7  10.6 = – 2.57.
1.4
Thus, a torque of 7 on the capping process curve corresponds to the point – 2.57 on the
standard Normal curve. The area to the left of 2.57 under the standard Normal curve is
0.995 (or 0.99491 if your prefer!), so the area to the right is 0.005, since the total area is
1. By symmetry, the area to the left of –2.57 is also 0.005 and, therefore, five caps per
thousand will be expected to be below the capping torque lower specification limit in
future production, provided the process remains stable. A simple statistical tool (a
‘control chart’) may be used to monitor the stability of manufacturing processes. Section
1.7 provides an introduction to and gives several examples of such charts.
Exercises
1.2.1.
Weight uniformity regulations usually refer to weights of tablets lying within a certain
range of the label claim. Suppose the weights (masses) of individual tablets are
Normally distributed with mean 100 mg (label claim) and standard deviation 7 mg.
(a)
If a tablet is selected at random, what is the probability that its weight is:
(i) less than 85 mg ?
(ii) more than 115 mg ?
(iii) either less than 85 mg or more than 115 mg ?
(b)
(i) What percentage of tablets lie between 90 mg and 110 mg ?
(ii) What percentage are heavier than 105 mg ?
(iii) What percentage are lighter than 98 mg ?
(c)
(i) What weight value K could be quoted such that 99% of all tablets are heavier than
K?
(ii) What weight values A and B can be quoted such that 99% of all tablets lie
between A and B ?
1.2.2
Figures 1.1.5 and 1.1.6 are based on data cited by Strike [5]. The data are urinary βhydroxycorticosteroid (β-OHCS) values in nmol/24h, obtained on a random sample of
100 obese adult females drawn from a fully specified target population. According to
1
Try re-calculating using standard deviations of 1.38 or 1.41 instead of 1.40 and note the effect on
the resulting probabilities. How often (never?) do engineers know standard deviations to this level of
precision?
Course Manual: PG Certificate in Statistics, TCD, Base Module
15
Strike it is of interest to define a 95% reference range for the β-OHCS measurements (a
reference interval encloses the central 95% of the population of measured values) that
can be used to assess the clinical status of future subjects drawn from the same
population. The distribution of β-OHCS values is quite skewed; accordingly, in order to
construct the reference interval we first transform the data to see if they can be
modelled by a Normal distribution in a transformed scale. Figure 1.1.6 suggests that
this is a reasonable assumption (this will be discussed further in Section 1.3). In the
log10 scale the mean is 2.7423 and the standard deviation is 0.1604.
(i)
(ii)
(iii)
Calculate the bounds (a, b) for the 95% reference interval in the log scale.
Use your results to obtain the corresponding reference interval in the original
measurement scale: the bounds will be (10a, 10b).
What value, U, should be quoted such that only 1% of women from this
population would be expected to have a β-OHCS measurement which exceeds U?
Calculating the standard deviation
Our calculations using the Normal curve assumed the mean and standard deviation
were already known. In practice, of course, they have to be calculated from observations
on the system under study. Suppose that a sample of n objects has been selected and
measured (e.g., SAT scores, people’s heights etc.) and the results are x1, x2, …xn.. The
average of these, x , gives an estimate of the corresponding population value, μ. The
standard deviation, s, of the set of results gives an estimate of the corresponding
population standard deviation, σ. This is calculated as:
n
s
 (x
i 1
i
 x)2
n 1
i.e. the mean is subtracted from each value, the deviation is squared and these squared
deviations are summed. To get the average squared deviation, the sum is divided by n–
1, which is called the 'degrees of freedom'2. The square root of the average squared
deviation is the standard deviation. Note that it has the same units as the original
measurements.
2
(n–1) is used instead of the sample size n for a mathematical reason; the deviations (before they are
squared) sum to zero, so once the sum of (n–1) is found, the last deviation is determined by the
constraint, thus, only (n–1) deviations are free to vary at random – hence, ‘degrees of freedom’.
Obviously, unless n is quite small, effectively the same answer is obtained if we get the average by
dividing by n.
Course Manual: PG Certificate in Statistics, TCD, Base Module
16
It is important always to distinguish between system parameters, such as the
population standard deviation, σ, and estimates of these parameters, calculated from
the sample data. These latter quantities are called ‘sample statistics’ (any number
calculated from the data is a ‘statistic’) and are themselves subject to chance variation.
System parameters, such as μ and σ, are considered fixed, though unknown, quantities.
In practice, if the sample size n is very large, the result calculated using the definition
given above will often be labelled σ, since a very large set of measurements will give the
'true' standard deviation. If the sample size is small, the result is labelled s (or
sometimes ˆ ); this makes clear to the user that the calculated value is itself subject to
measurement/sampling error, i.e. if the study were repeated a different value would be
found for the sample standard deviation.
Aside: The Coefficient of Variation (CV) is defined as the standard deviation divided by the
mean. It is often useful to compare standard deviations computed from different distributions.
The assumption that the parameters of the Normal distribution are known without
error is reasonable for the height data of Example 1 (where n=1794), but clearly the
sample size for the capping torque data (n=78) is such that we cannot expect that the
‘true’ process mean or standard deviation is exactly equal to the sample value. Methods
have been developed (tolerance intervals) to allow for the uncertainty involved in having
only sample data when carrying out calculations like those of Examples 1 and 2, though
these are rarely discussed in elementary textbooks. Hahn and Meeker [6] discuss such
intervals in an engineering context.
1.3
Assessing Normality
The statistical methods that will be discussed in later chapters assume that the data
come from a Normal distribution. This assumption can be investigated using a simple
graphical technique, which is based on the type of calculation discussed in the previous
section. Here, for simplicity, the logic of the method will be illustrated using a sample of
10 values, but such a sample size would be much too small in practice, as it would
contain little information on the underlying shape, particularly on the shapes of the
tails of the curve.
The relation between any arbitrary Normal value x and the corresponding standard
Normal value z is given by:
z
x

which using the inverse transformation can be re-written as:
Course Manual: PG Certificate in Statistics, TCD, Base Module
17
x = μ + σ × z.
If x is plotted on the vertical axis and z on the horizontal axis, this is the equation of a
straight line with intercept μ and slope σ, as shown in Figure 1.3.1. Accordingly, if we
make a correspondence between the x values in which we are interested and z values
from the standard Normal table and obtain a straight line, at least approximately, when
they are plotted against each other, we have evidence to support the Normality
assumption.
X

0
Z
Figure 1.3.1: The theoretical relationship between x and z when x is Normal
x
12.6
13.1
9.8
11.7
10.6
11.2
12.2
11.1
8.7
10.5
Ranks Fraction  x
i
i/n
9
10
2
7
4
6
8
5
1
3
0.9
1.0
0.2
0.7
0.4
0.6
0.8
0.5
0.1
0.3
z
i 3/8
n 1 / 4
Nscores
1.282

-0.842
0.524
-0.253
0.253
0.842
0.000
-1.282
-0.524
0.841
0.939
0.159
0.646
0.354
0.549
0.744
0.451
0.061
0.256
1.000
1.547
-1.000
0.375
-0.375
0.123
0.655
-0.123
-1.547
-0.655
Table 1.3.1 Sample data for calculating Normal Scores
Course Manual: PG Certificate in Statistics, TCD, Base Module
18
The correspondence is established by finding the fraction of the x values equal to or less
than each value in the dataset, and then finding the z value that has the same fraction
of the standard Normal curve below it. In Table 1.3.1, the ten x values are listed in
column 1, their ranks, i, (smallest 1 to largest n=10) in column 2, the fraction equal to or
less than x in column 3 (i/n). Column 4 gives the z value with the area given by column
3 below it; for example, in the first row, 90% of the sample values are equal to or less
than x=12.6 and column 4 indicates that 90% of the area under a standard Normal
curve is below 1.282 (Table ST-1 gives z values to two decimal places, but software such
as Minitab or Excel will give more, if required).
This method for establishing the correspondence between x and z will always result in
the largest x value corresponding to z=  (which presents a challenge when plotting!).
To avoid the infinity, some small perturbation of the calculation of the fraction i/n is
required, such that the result is never i/n=1. Simple examples of possible perturbations
would be (i–0.5)/n or i/(n+0.5). Minitab has several options; (i–3/8)/(n+1/4), which is
based on theoretical considerations, is used in Table 1.3.1. The areas which result from
this are shown in column 5 and the corresponding z values (Normal scores) in column 6.
The choice of perturbation is not important: all that is required is to draw a graph to
determine if the values form an approximately straight line. We do not expect a
perfectly straight line even for truly Normal data, due to the effect of sampling
variability. Thus, 12.6 is the ninth largest value in our dataset, but any value between
13.1 and 12.2 would also have been the ninth largest value. Consequently, 12.6 is not
uniquely related to 0.841.
Figure 1.3.2 shows the Normal plot (or Normal probability plot, as it is also called) for
our dataset – a ‘least squares’ line is superimposed to guide the eye (we will discuss
such lines later). The data are close to the line (hardly surprising for an illustrative
example!).
15
Mean
StDev
N
AD
P-Value
14
11.15
1.328
10
0.131
0.971
13
X
12
11
10
9
8
-2
-1
0
Score
1
2
Figure 1.3.2: Normal plot for the sample data
Course Manual: PG Certificate in Statistics, TCD, Base Module
19
Departures from Normality
The schematic diagrams in Figure 1.3.3 indicate some patterns which may be expected
when the underlying distribution does not conform to the Normal curve. Plots similar
to Figure 1.3.3(a) will be encountered commonly, as outliers are often seen in real
datasets. Figure 1.3.3(c) might, for example, arise where the data represent blood
measurements on patients - many blood parameters have skewed distributions. Figures
1.3.3(b) and (d) are less common but (b) may be seen where the data are generated by
two similar but different sources, e.g. if historical product yields were being studied and
raw materials from two different suppliers had been used in production. The term
‘heavy tails’ refers to distributions which have more area in the tails than does the
Normal distribution (the t-distribution is an example). Heavy tails mean that data
values are observed further from the mean, in each direction, more frequently than
would be expected from a Normal distribution.
Single outlier
(a)
Mixture
(b)
Skewness
(c)
Heavy tails
(d)
Figure 1.3.3: Idealised patterns of departure from a straight line
Real Data
In Section 1.1 we examined histograms for a number of datasets; here, we draw Normal
plots for several of those examples. Figure 1.3.4 is the Normal plot for the SAT scores of
Figure 1.1.1, while Figure 1.3.5 is the Normal plot for the capping torques of Figure
1.1.2. In both cases the lines formed by the plotted points are essentially straight. The
plots also contain statistical significance tests (the Anderson-Darling test, hence AD)
which test for Normality. We will discuss statistical tests in the next chapter. Here, we
use a rule of thumb which says that a p-value (p-values vary between 0 and 1) greater
than 0.05 supports Normality, while one less than 0.05 rejects it. For both Normal plots
the p-values are large and there is no reason to question the assumption of Normality.
Course Manual: PG Certificate in Statistics, TCD, Base Module
20
Mean
StDev
N
AD
P-Value
800
595.6
73.21
200
0.259
0.712
Verbal
700
600
500
400
300
-3
-2
-1
0
Score
1
2
3
Figure 1.3.4: Normal plot for SAT Verbal scores for 200 university students
15
14
13
Mean
StDev
N
10.84
1.351
78
AD
P-Value
0.206
0.865
Torque
12
11
10
9
8
7
6
-3
-2
-1
0
Score
1
2
3
Figure 1.3.5: Normal plot for Capping torques for 78 screw-capped containers
Figure 1.3.6 refers to the Urinary β-OHCS measurements, which we first encountered
in Figure 1.1.5. The graph is far from straight and the AD p-value is very much less
than 0.05; the graph displays the characteristic curvature of a right-skewed
distribution. Figure 1.3.7 is the Normal plot of the log-transformed data and it is quite
consistent with an underlying Normal distribution.
Course Manual: PG Certificate in Statistics, TCD, Base Module
21
1600
Mean
StDev
N
AD
P-Value
1400
1200
590.8
224.0
100
1.729
<0.005
b-OHCS
1000
800
600
400
200
0
-3
-2
-1
0
Score
1
2
3
Figure 1.3.6: Normal plot for Urinary β-OHCS measurements
Mean
StDev
N
AD
P-Value
3.2
Log10(b-OHCS)
3.0
2.742
0.1604
100
0.250
0.738
2.8
2.6
2.4
2.2
-3
-2
-1
0
Score
1
2
Figure 1.3.7: Normal plot for log-transformed
3
-OHCS measurements
Figure 1.3.8 is a Normal plot of the women’s heights measurements of Figure 1.1.4.
Although it is very close to a straight line, it has a curiously clumped, almost stair-like,
appearance. The p-value is very small indeed. The reason for this is that the
measurements are rounded to integer values (centimetres) and, because the dataset is
so large, there are many repeated values. A Normal distribution is continuous (the
sampled values can have many decimal places) and few, if any, repeated values would
be expected to occur; the AD test detects this unusual occurrence. To illustrate the
effect of rounding on the plots, 1794 random numbers were generated from a Normal
distribution with the same mean and standard deviation as the real data (the mean and
SD of the sample generated are slightly different from those specified, due to sampling
variability).
Course Manual: PG Certificate in Statistics, TCD, Base Module
22
190
Mean
StDev
N
AD
P-Value
Heights (cm)
180
162.4
6.284
1794
2.985
<0.005
170
160
150
140
-3
-2
-1
0
Score
1
2
3
Figure 1.3.8: Normal plot for women’s heights measurements
190
Mean
StDev
N
AD
P-Value
Simulate-1
180
162.2
6.409
1794
0.417
0.330
170
160
150
140
-3
-2
-1
0
Score
1
2
3
Figure 1.3.9: Normal plot for simulated women’s heights measurements
Figure 1.3.9 shows a Normal plot for the data generated; as expected from random
numbers, the sample values give a very good Normal plot. The data were then rounded
to whole numbers (centimetres) and Figure 1.3.10 was drawn – its characteristics are
virtually identical to those of the real data, showing that the cause of the odd line is the
rounding; note the change in the p-value in moving from Figure 1.3.9 to Figure 1.3.10.
Figure 1.3.11 shows a Normal plot for the Iris data of Figure 1.1.3 – the effect of the
measurements being rounded to only one decimal place, resulting in multiple petals
having the same length, is quite striking.
Course Manual: PG Certificate in Statistics, TCD, Base Module
23
190
Mean
StDev
N
AD
P-Value
Round(Simlate-1)
180
162.2
6.413
1794
2.133
<0.005
170
160
150
140
-3
Figure 1.3.10:
measurements
-2
-1
Normal
plot
0
Score
for
1
2
rounded
3
simulated
Mean
StDev
N
AD
P-Value
1.9
1.8
Petal Length
1.7
women’s
heights
1.464
0.1735
50
1.011
0.011
1.6
1.5
1.4
1.3
1.2
1.1
1.0
-2
-1
0
Score
1
2
Figure 1.3.11: Normal plot for Iris petal lengths
The assumption of data Normality underlies the most commonly used statistical
significance tests and the corresponding confidence intervals. We will use Normal plots
extensively in verifying this assumption in later chapters.
Exercises
1.3.1.
For the data in Exercise 1 in Chapter 0 (use Excel if you wish):
(a) Combine the values in the first 3 columns together in one dataset, compute the Normal
Score Table and plot these on a Normal Plot.
(b) Repeat part (a) for the 20 mean values of the variables x1 to x20.
(c) Contrast the plots in (a) and (b); in particular, what is the effect of averaging?
Course Manual: PG Certificate in Statistics, TCD, Base Module
24
1.4 Combining Random Quantities (Important)
Often the quantities in which we are interested are themselves the result of combining
other quantities that are subject to chance variation. For example, a journey is
composed of two parts: X is the time it takes to travel from A to B, and Y is the time to
travel from B to C. We are interested in S, the sum of the two travel times.
If we can assume that X is distributed with mean 𝜇𝑥 = 100 and standard deviation
𝜎𝑥 = 10 and (units are minutes), while Y is distributed with mean mean 𝜇𝑦 = 60 and
standard deviation 𝜎𝑦 = 5, what can we say about the total travel time, S=X+Y?
If we can assume that X and Y are independent (i.e., if X happens, for example, to be
unusually long, this fact carries no implications for Y being either unusually long or
short), then the following rules hold.
Addition Rules (S = X+Y)
Means and Variances add
Mean:
𝝁𝒔 = 𝝁𝒙 + 𝝁𝒚
Variance: 𝝈𝟐𝒔 = 𝝈𝟐𝒙 + 𝝈𝟐𝒚
The underlying mathematics shows that both the means and the variances (the squares
of the standard deviations) are additive. The standard deviation of the overall travel
time, S, is:
Standard Deviation of a Sum: 𝝈𝑺 = √𝝈𝟐𝒙 + 𝝈𝟐𝒚
We might also ask, how much longer than the trip from B to C, the trip from A to B is
likely to take (i.e., what can we say about D=X–Y). To answer such questions we need
subtraction rules.
Subtraction Rules (D = X-Y)
Mean:
𝝁𝑫 = 𝝁𝒙 − 𝝁𝒚
Variance: 𝝈𝟐𝑫 = 𝝈𝟐𝒙 + 𝝈𝟐𝒚
Course Manual: PG Certificate in Statistics, TCD, Base Module
25
Note that the variances add, even though we are subtracting. This gives:
Standard Deviation of a Difference: 𝝈𝑫 = √𝝈𝟐𝒙 + 𝝈𝟐𝒚
The independence assumption is required for the rules related to the standard
deviation; it is not required for combining means.
Normality Assumptions
The rules given above hold irrespective of the distributions that describe the chance
variation for the two journeys, X and Y. However, if we can assume that X and Y are
Normally distributed, then any linear combination of X and Y (sums or differences,
possibly multiplied by constants) will also be Normally distributed. In such cases, the
calculations required to answer our questions are simple; they are essentially the same
as for Examples 1 and 2, once we have combined the component parts into the overall
measured quantity, and then found its mean and standard deviation using the above
rules.
Example 3
Given our assumptions above about the means and standard deviations of the two
journey times, X and Y, and assuming also that journey times are Normally distributed,
what is the probability that the overall journey time, S,
(i)
(ii)
(i)
will take more than three hours (S > 180 minutes)?
will take less than 2.5 hours (S < 150 minutes)?
From our addition rules we obtain:
Mean:
𝜇𝑠 = 𝜇𝑥 + 𝜇𝑦 = 100 + 60 = 160
Variance: 𝜎𝑠2 = 𝜎𝑥2 + 𝜎𝑦2 = 102 + 52 = 125
𝜎𝑆 = √𝜎𝑥2 + 𝜎𝑦2 = √125 = 11.18
Overall travel times are, therefore, Normally distributed with a mean of 160 and a
standard deviation of 11.18, as shown schematically in Figure 1.4.1.
Course Manual: PG Certificate in Statistics, TCD, Base Module
26
Figure 1.4.1: The standard Normal curve and the travel times curve
The probability that S is more than 180 minutes is given by:
P( S  180)  P( Z 
180   S
S
)  P( Z 
180  160
)  P( Z  1.79)
11.18
 1  P( Z  1.79)  1  0.9633  0.0367
The probability that the overall travel time, S, exceeds three hours (180 minutes)
is approximately 0.04, as illustrated schematically in Figure 1.4.1.
(ii)
Figure 1.4.2: The standard Normal curve and the travel times curve
Course Manual: PG Certificate in Statistics, TCD, Base Module
27
P( S  150)  P( Z 
150   S
S
)  P( Z 
150  160
)
11.18
 P(Z  0.89)  P(Z  0.89)  1  P(Z  0.89)  0.19
The probability that the overall journey, S, will take less than 2.5 hours (150
minutes) is 0.19, as illustrated schematically in Figure 1.4.2.
Example 4
Suppose that X (as given in the introduction, i.e. mean 𝜇𝑥 = 100 and standard deviation
𝜎𝑥 = 10 (units are minutes)) is the time it takes a part-time student to travel to college
each evening and she makes ten such trips in a term.
(i)
If T is the total travel time to college for the term, what are the mean and
standard deviation for T?
(ii)
What is the probability T exceeds 18 hours (1080 minutes)?
Since only one trip type is involved, we do not need the X sub-script. We have:
𝜇𝑥 = 𝜇 = 100
𝜎𝑥 = 𝜎 = 10
The total travel time is:
10
T   Xi
i 1
where Xi is the journey time for trip i and i = 1, 2, 3…10.
All trips have the same characteristics, so 𝜇𝑖 = 100 and 𝜎𝑖 = 10.
(i)
Using the addition rules
𝜇𝑇 = 𝜇1 + 𝜇1 + ⋯ + 𝜇10 = 10 × 100 = 1,000
2
𝜎𝑇2 = 𝜎12 + 𝜎22 + ⋯ + 𝜎10
= 10 × (102 ) = 1,000
2
𝜎𝑇 = √𝜎12 + 𝜎22 + ⋯ + 𝜎10
= √1,000 = 31.62
Total travel time is Normally distributed with a mean of 1000 and a standard deviation
of 31.62, where the units are minutes.
Course Manual: PG Certificate in Statistics, TCD, Base Module
28
(ii)
Figure 1.4.3: The standard Normal curve and the total travel time curve
1080  1000
)  P(Z  2.53)
31.62
 1  P(Z  2.53)  1  0.9943  0.0057
P(T  1080)  P(Z 
The chances that her total travel time to college for the term might exceed 18
hours (1080 minutes) is only about 6 in a thousand, as illustrated schematically in
Figure 1.4.3. Note that the travel characteristics for travelling back from college
could be quite different (different times might mean different traffic levels), so this
would need examination if we were interested in her total amount of college travel.
Exercises
1.4.1.
A final year psychology student approaches a member of staff seeking information on
doing a PhD. In particular, she is concerned at how long it will take. The staff member
suggests that there are essentially four sequential activities involved: Literature Review
(reading and understanding enough of the literature in a particular area to be able to say
where there are gaps that might be investigated), Problem Formulation (stating precisely
what will be investigated, how this will be done, what measurement instruments will be
required, what kinds of conclusions might be expected), Data Collection (developing the
necessary research tools, acquiring subjects, carrying out the data collection, carrying out
the statistical analysis), and Writing up the results (drawing conclusions, relating them
to the prior literature and producing the final thesis). She points out that the required
times are variable, but that her experience suggests that they can be modelled by a
sequence of independent Normal distributions with the parameters shown in Table 1.4.1,
where the time units are weeks.
Course Manual: PG Certificate in Statistics, TCD, Base Module
29
Activity
Mean
Standard
Deviation
Literature review (L)
Problem formulation
(P)
Data collection (D)
Write up (W)
30
10
8
3
120
16
12
3
Table 1.4.1: Estimates for the means and SDs of the four activities (weeks)
Assuming that this is a reasonably accurate description of the situation (in practice, of
course, the activities will overlap), what is the probability that the doctorate will take (i)
less than 3 years (156 weeks)?; (ii) more than 3.5 years (182 weeks)?; (iii) more than 4
years (208 weeks)?
1.5 The effects of averaging
It is rarely the case that decisions are based on single measured values – usually,
several values are averaged and the average forms the basis of decision making. We
need, therefore, to consider the effect of averaging on our data. We will discuss this in
the context of measuring the percentage dissolution of tablets after 24 hours in a
dissolution apparatus. The ideas are general though; precisely the same statements
could be made about examination results, prices of second-hand cars or the pH
measurements made on samples of lake water.
Figure 1.5.1 illustrates the averaging effect. Figure 1.5.1(a) is an idealised histogram of
individual tablet measurements; it represents what we might expect to get by drawing a
histogram for many thousands of measurements of the percentage dissolution of
individual tablets. Because of the large number of observations, the bars of the
histogram could be made very narrow and a smooth curve would be expected to fit the
histogram very closely. In practice, of course, we would rarely have such a large
quantity of data available to us, but that does not prevent us from visualising what
would happen under idealised conditions.
The data on which Figure 1.5.1(b) is based are no longer single tablet dissolution values.
Suppose we randomly group the many thousands of tablet measurements into sets of
four, calculate the mean for each set, and draw a histogram of the means. Four values
selected at random from the distribution described by (a) will, when averaged, tend to
give a mean result close to the centre of the distribution. In order for the mean to be
very large (say greater than 92) all four of the randomly selected tablet measurements
Course Manual: PG Certificate in Statistics, TCD, Base Module
30
would have to be very large, an unlikely occurrence3. Figure 1.5.1(b) represents an
idealised version of this second histogram. Of course we would never undertake such an
exercise in the laboratory, though we might in the classroom (using simulation). The
implications of the exercise are, however, very important. Figure 1.5.1 shows that the
properties of means are very different from those of single measurements in one key
aspect: they are much less variable. This difference is important, since virtually all
data-driven decision making relies on means rather than on single measurements. The
narrower curve is called ‘the sampling distribution of the mean’, as it describes the
variation of means, based on repeated sampling, and its standard deviation is called ‘the
standard error of the mean’ or ‘standard error’ for short.
(b)
(a)
86.5
87.5
88.5
89.5
90.5
91.5
92.5
93.5
Figure 1.5.1: Idealised histograms of the distributions of percentage dissolution
of (a) individual tablets; and (b) of the averages of 4 tablets.
Mathematical theory shows that, if the standard deviation of the distribution of
individual values is σ then the standard error of the distribution of sample means is
σ/n, where n is the number of independent values on which each sample mean is based.
Suppose the individual values vary about a long-run average value of 90 with a
standard deviation of 0.5. It follows that averages of 4 values will also vary about a
long-run mean of 90, but their standard error will be 0.25. Recall that approximately
95% of the area under any Normal curve lies within two standard deviations (or
standard errors) of the mean. This implies that while 95% of individual tablet
measurements would be between 89 and 91, 95% of means of 4 tablet measurements
would be between 89.5 and 90.5. Thus, the effect of the averaging process is that a
sample mean result is likely to be closer to the long-run or batch average, than a
3
If the probability that one tablet was greater than 92 was 0.05, the probability that all four would be
greater than 92 would be 0.00000625!
Course Manual: PG Certificate in Statistics, TCD, Base Module
31
randomly selected single tablet measurement would be. This gain in precision is the
reason why we base decisions on means, in practice.
Example 4 revisited
(i)
Suppose we take the journey times to be a sample of size n = 10 journey times
and label journey time as 𝑥1 = 10, 𝑥2 = 10, ⋯ 𝑥10 = 10, (i.e each has a journey
is equal – a rather odd sample indeed).
What is the value of 𝑥̅ the overall average travel time to college based on this
sample and what is its standard deviation (i.e. standard error) assuming the
standard deviation of a single journey time is 𝜎 = 10 minutes?
(ii)
What is the probability 𝑥̅ exceeds 18 hours (1080 minutes)?
Answer
(i)
Using the addition rules for random variables the overall sample mean travel
time is for the 10 observed random journey times is:
x
1
n
n

i 1
Xi 
1
10
10
X
i 1
i
=
100
10
= 10
where Xi is the journey time for trip i and i = 1, 2, 3…10.
The standard error is the standard deviation of 𝑥̅
𝜎𝑥̅2
𝑛
10
𝑖=1
𝑖=1
1
1
10 × (102 )
= 2 ∑ 𝜎𝑖2 = 2 ∑ 𝜎 2 =
= 10
𝑛
10
100
since each 𝑥𝑖 has the same standard deviation
giving
𝜎𝑥̅ = √10 = 3.16
NB: the
𝟏
𝒏𝟐
in the formula above – this appears because the variance has the
effect of squaring constants so the
𝟏
𝒏𝟐
Course Manual: PG Certificate in Statistics, TCD, Base Module
𝟏
𝒏
factor in the mean formula changes to
32
(ii) What is the probability the average travel time 𝑥̅ exceeds 15 minutes?
15  10
)  P( Z  1.58)
3.16
 1  P( Z  1.58)  1  0.943  0.057
P( x  15)  P( Z 
The chances that her average travel time to college for the term might exceed minutes is
only about 6 in a hundred.
The histograms/curves of Figure 1.5.1 are Normal (probably a reasonable assumption
for tablet dissolution). However, what has been described does not depend on the
assumption of an underlying Normal distribution. Even if the curve for individual
tablets had been skewed, the mean of the sampling distribution would be the same as
that of the individual tablets and the standard error would still be σ/n. What is
interesting, though, is that, as the number of measurements on which each mean is
based increases, the shape of the sampling distribution approaches that of a Normal
curve, even when the underlying distribution shape is non-Normal.
We will illustrate this interesting and important result using some data simulated from
a skewed distribution, specifically from a chi-square distribution with 7 degrees of
freedom (we will encounter the chi-square distribution later when we discuss
significance tests; here, it is used simply as a typically skewed distribution curve).
Figure 1.5.2 shows the theoretical curve, while Figure 1.5.3 shows a histogram of 200
values randomly generated from this distribution.
Figure 1.5.2: A chi-square curve with 7 degrees of freedom
Course Manual: PG Certificate in Statistics, TCD, Base Module
33
50
Frequency
40
30
20
10
0
0
4
8
12
16
20
24
Figure 1.5.3: Histogram of 200 values from a chi-square curve with 7 degrees of
freedom
Figure 1.5.4 shows the corresponding Normal plot which has the characteristic curved
shape, we saw previously for skewed distributions.
25
Mean
StDev
N
AD
P-Value
Simulated Data
20
7.485
4.007
200
3.856
<0.005
15
10
5
0
-5
-3
-2
-1
0
Score
1
2
3
Figure 1.5.4:Normal plot of 200 values sampled from a chi-square curve with 7 degrees
of freedom
Thirty values were randomly generated from this distribution and the mean was
obtained. This was repeated 200 times, resulting in a set of 200 sample means, each
Course Manual: PG Certificate in Statistics, TCD, Base Module
34
based on n=30. A histogram of these means is shown in Figure 1.5.5, while Figure 1.5.6
represents a Normal plot of the set of 200 means.
50
Frequency
40
30
20
10
0
5
6
7
8
9
Mean
Figure 1.5.5: Histogram of 200 means each based on 30 values sampled from a chisquare curve with 7 degrees of freedom
Mean
StDev
N
AD
P-Value
9
Mean
8
6.939
0.7326
200
0.211
0.858
7
6
5
4
-3
-2
-1
0
Score
1
2
3
Figure 1.5.6: Normal plot of 200 means each based on 30 values sampled from a chisquare curve with 7 degrees of freedom
The effect of averaging has been particularly successful here in producing means which
closely follow a Normal distribution (not all samples will be quite so good). The
mathematical theory says that as the sample size tends to infinity, the means become
Normal; it is clear, though, that even with a sample size of 30 in this case, the so-called
Normal approximation is very good. In statistical theory the Normal approximation is
called the Central Limit Theorem (CLT); these will be used interchangeably. The
importance of the Normal approximation/CLT cannot be over-emphasised.
Course Manual: PG Certificate in Statistics, TCD, Base Module
35
In pathological cases (e.g., extremely skewed distributions)4 the sampling distribution
curve will not be Normal for the moderate sample sizes that are likely to be used in
practice. In most cases, however, where the underlying curve is not too far from a
Normal curve, the sampling distribution will be reasonably close to a Normal curve, and
this allows us use statistical methods based on the assumption of Normality. Apart
from its common occurrence in practice (as seen in several examples in Section 1.1) this
property of sampling distributions is the reason why the Normal curve is so important
in statistics.
1.6
Measurement Systems
The same symmetrical characteristics as seen for the data of Section 1.1 are displayed
in Figure 1.6.1, but it is different in one important respect – the picture is based on 119
repeated measurements of the same pharmaceutical material, whereas all our earlier
examples were based on single measurements on different people or objects. The
material measured was a control material used in monitoring the measurement process
in a quality control analytical laboratory in a pharmaceutical manufacturing company
[See Mullins [7] Chapters 1, 2]. The methods discussed in Section 1.3 show that a
Normal curve is a good model for these data, also.
95.4
96.0
96.6
97.2
97.8
Figure 1.6.1: Repeated potency (%) measurements on a control material
In using the Normal curve in a measurement context we have a different conceptual
model for our data than that for the previously cited examples. Where the numbers
referred to different physical entities (whether these were people, industrial components
or flowers) the curves refer to variation between those units – some entities give values
much higher or lower than others, but most cluster in the centre. For measurement
systems we do not have a physical distribution; we have an hypothetical distribution of
the many thousands of measurements that might be made on the single physical entity
4
In particular, theoretically the Normal approximation fails for the Cauchy Distribution.
Course Manual: PG Certificate in Statistics, TCD, Base Module
36
that is to be measured. In practice, of course, the vast majority of these measurements
will never be made, so our questions about the ‘system’ of measurements (or the
measurement process) are somewhat abstract in nature, but we are so accustomed to
dealing with measurements that this abstraction often goes un-discussed. Two aspects
of measurement quality are illustrated by Figure 1.6.2, namely bias and precision.
A
B
95
Figure 1.6.2:
systems
100
105
110
115
Measurements on the same entity by two measurement
Suppose this picture represents smoothed histograms, based on thousands of
measurements made on the same object/material by two different measurement systems
A, B. It is clear that System A gives lower values, on average, i.e., the long-run mean
for A is smaller than that for B5, μA < μB. System A is said to be biased downwards
relative to System B. Which system gives the ‘right’ results, on average, (i.e., is
unbiased) we cannot know unless there is a measurement ‘gold standard’. When a
benchmark measurement exists we can define how accurate the system is relative to the
benchmark.
The spread of measurements for System B is greater than that for A – A is said to have
better precision. The width of each curve is measured by the standard deviation, σ; the
shapes of the curves in Figure 1.6.2 mean that σA < σB. There is no necessary
relationship between the two parameters. There is no reason why σA could not be bigger
than σB.
Figure 1.6.3 [7, 8] shows serum ALT6 concentrations for 129 adults. It demonstrates
that there is no necessary relationship between the shape of the curve describing
5
Long-run averages only make sense when the system or process is stable, accordingly care should be taken to
ensure stability before a long-run average is computed.
6
Alanine aminotransferase (ALT) is an enzyme found in most human tissue.
Course Manual: PG Certificate in Statistics, TCD, Base Module
37
variation in the physical system under study and the shape of the curve that describes
variation in the measurement system used to measure the physical entities. The ALT
distribution (Figure 1.6.3(a)) is right-skewed, that is, it has a long tail on the right-hand
side, which means that some individuals have much higher ALT levels than the
majority of the population.
Figure 1.6.3:
specimen
Distributions of ALT results (a) 129 adults (b) 109 assays of one
Figure 1.6.3(b) shows the distribution of results obtained when one of the 129 serum
specimens was re-analysed 109 times. The shape of the distribution that describes the
chance analytical variability is very different from that which describes the overall
variation in ALT measurements. It suggests that a Normal distribution might well
describe the analytical variability. If, therefore, we were interested in studying the
analytical procedure – for, example, to quantify the precision, which is obviously poor –
we might work directly in the arithmetic scale (i.e., the scale in which the
measurements were made. On the other hand, if we wished to make statements about
the distribution of ALT concentrations in the population from which the subjects derive
(by obtaining a reference interval, for example), then we might choose to transform the
data before proceeding with our analysis (in order to get a Normal curve which is easier
to analyse).
Figures 1.6.1 and 1.6.3 underline the importance of the Normal curve for the analysis of
measurement systems, as the graphs of Section 1.1 showed its importance for describing
chance variation in different physical populations.
Course Manual: PG Certificate in Statistics, TCD, Base Module
38
Exercises
1.6.1.
1.6.2.
(i)
An unbiased analytical system is used to measure an analyte whose true value
for the parameter measured is 100 units. If the standard deviation of repeated
measurements is 0.80 units, what fraction of measurements will be further than
one unit from the true value? Note that this fraction will also be the probability
that a single measurement will produce a test result which is either less than 99
or greater than 101, when the material is measured. What fraction of
measurements will be further than 1.5 units from the true value? Give the
answers to two decimal places.
(ii)
Suppose now that the analytical protocol requires making either 2 or 3
measurements and reporting the mean of these as the measured value.
Recalculate the probabilities for an error of one unit and compare them to those
obtained for a single measurement.
(i)
A trawl through the website HorsesForum.com suggests that a nailed-on steel
horseshoe will last about 5 to 8 weeks before it needs to be re-set. Assuming the
lifetime of a horseshoe is normally distributed with population mean μ = 7 weeks
and standard deviation σ = 1.25 weeks what is the probability that a nailed-on
horseshoe picked at random from the population will last 9 or more weeks before
needing re-set
(ii)
A second website ‘The Chronicle of the Horse’ advises so-called ‘glued-on’
horseshoes, that is shoes that are glued rather than nailed-on, may be used in
cases of laminitis (aka white line disease in USA) where the hoof is unable to
accommodate nails. Gleaning the posts on the website seems to indicate that the
population mean lifetime of glued-on shoes is μ = 5 weeks with standard
deviation σ = 2.0 weeks. Assuming the lifetimes are normally distributed what is
the probability that a glued-on horseshoe picked at random from the population
will last 9 or more weeks before needing re-set.
(iii)
Comparing the information from the two websites: What is the probability that a
nailed-on horseshoe will last longer than a glued-on horseshoe, i.e the difference
between the lifetimes of the two types of horseshoe is greater than zero.
(iv)
Comparing a sample mean to a population value μ (e.g population mean):
The website data used in part (i) was in fact based on a sample of n=5 with
𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 = 7. On the basis of this sample data what is the probability that the
mean lifetime μ for (the population of) nailed-on horseshoes is at least (μ =) 9
weeks.
Course Manual: PG Certificate in Statistics, TCD, Base Module
39
(v)
1.6.3.
Exam style question:
Comparing the information based on samples from the two websites: The website
data used in part (i) was in fact based on a sample of n=5 with 𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 = 7
while in part (ii) the sample size was n=2 and 𝑥̅𝐺𝑙𝑢𝑒𝑑−𝑜𝑛 = 5. On the basis of these
sample sizes what is the probability that a nailed-on horseshoe will last longer
than a glued-on horseshoe, i.e the difference between the means of the lifetimes of
the two types of horseshoe is greater than zero.
Combining data - Meta-analysis study
(i)
In a 3-rd world country in Latin America a study shows that infants born to
families who cook on an open Wood stove have an average birth weight of μ = 2.9
kg with standard deviation 𝜎 = 0.5kg.
What is the probability that an infant born to one of these families is over 3.6kg?
(ii)
Cooking in the country is also done an open fires and electric cookers in this
country. The respective average birth weight statistics are μ = 2.8kg and 3.1kg
while the standard deviations are 0.4kg and 1.3kg respectively.
Repeat part (i) for an electric stove.
(iii)
Combining the information on cooking types: What is the probability that an
infant born in this country will be less than 2.3kg.
(iv)
Combining the information on cooking types based on samples from the three
cooking type studies: The study data used in parts (i) and (ii) was in fact based on
3 samples each of size n=36 (108 in all). Taking the sample mean in each case to
be the population mean (i.e. with 𝑥̅ = 𝜇) repeat part (iii) above and comment.
Course Manual: PG Certificate in Statistics, TCD, Base Module
40
1.7 Appendix: Case Study Statistical Process Control Charts
In this chapter we have discussed various aspects of the Normal curve as a model for
statistical variation. This final section illustrates the use of a graphical tool for
monitoring the stability of a system. This tool, the control chart, is based on the
properties of the Normal curve and is an example of a powerful practical tool based on
simple underlying ideas.
Statistical process control (SPC) charts were introduced for monitoring production
systems but, as we shall see, they have much wider applicability. Conceptually they are
very simple: a small sample of product is taken regularly from the process and some
product parameter is measured. The values of a summary statistic (such as the sample
mean) are plotted in time order on a chart; if the chart displays other than random
variation around the expected result it suggests that something has changed in the
process. To help decide if this has happened control limits are plotted on the chart: the
responses are expected to remain inside these limits. Rules are decided upon which will
define non-random behaviour.
The most commonly used charts were developed by Shewhart [9] in Bell Laboratories in
the1920’s. He described variation as being due either to ‘chance causes’ or ‘assignable
causes’. Chance causes are the myriad of small influences that are responsible for the
characteristic Normal shape, which we saw in a variety of settings in Section 1.1.
Shewhart’s crucial insight was that stability must be understood in the context of this
inevitable chance variation, not in the commonplace notion of ‘unchange’. Assignable
causes are larger: they tend to change the mean or the standard deviation of a process
distribution. If a process is stable such that it exhibits only random variation around a
given reference value and the size of that variation (as measured by the standard
deviation) remains constant, Shewhart described it as being ‘in statistical control’ or
simply ‘in control’. The objective in using control charts is to achieve and maintain this
state of statistical control. Control charts were developed to control engineering
production processes, but, as Charts 2, 3 and 4 will show, they can be applied just as
effectively to measurement systems. Any apparent differences between the two
situations disappear when we think of a measurement system as a production process
whose output is measurements. Chart 5 illustrates the use of a control chart in a retail
sales setting.
For an extensive discussion of control charts in a manufacturing environment see
Montgomery [10]. For an introduction to the use of control charts for monitoring
measurement systems see Mullins [7]. Stuart [11] gives a less technical introduction to
Course Manual: PG Certificate in Statistics, TCD, Base Module
41
control charts in industry than does Montgomery; he also discusses their application in
a retail business context (see Chart 5, which is ‘borrowed’ from Stuart!).
Chart 1: Monitoring Production Systems
Figure 1.7.1 shows a control chart for a critical dimension (mm) of moulded plastic
medical device components, each of which contained a metal insert purchased from an
outside supplier.
Twenty five samples of size n=5 were taken from the stream of parts manufactured over
a period of several weeks, with a view to setting up control charts to monitor the
process. The five sample results were averaged and it is the average that is plotted in
the chart. Sample means are usually denoted x , where x denotes a single measured
value, for this reason the chart is called an ‘X-bar chart’. For now, the centre line (CL)
and control limits (upper and lower control limits, UCL and LCL) will be taken as given;
later, the rationale for the limits will be discussed.
3.70
UCL=3.6713
Sample Mean
3.65
3.60
_
_
X=3.5537
3.55
3.50
3.45
LCL=3.4361
1
3
5
7
9
11
13 15
Sample
17
19
21
23
25
Figure 1.7.1: An X-bar chart for the moulded plastic components
In using control charts different companies/users apply different rules to identify
instability. For example, the SPC manual of the Automotive Industry Action Group [12]
(AIAG: a task force set up by the Ford, Chrysler and General Motors companies to unify
their SPC procedures) suggests that action is required if any of the following occur:
•
any point outside of the control limits;
•
a run of seven points all above or all below the central line;
•
a run of seven points in a row that are consistently increasing (equal to or greater
than the preceding points) or consistently decreasing;
Course Manual: PG Certificate in Statistics, TCD, Base Module
42
•
any other obviously non-random pattern.
Runs of nine points, rather than seven, are also commonly recommended. The same
basic principle underlies all the rules: a system that is in statistical control should
exhibit purely random behaviour - these rules correspond to improbable events on such
an assumption. Accordingly, violation of one of the rules suggests that a problem has
developed in the process and that action is required. The rationale for the rules is
discussed below.
The manufacturing process to which Figure 1.7.1 refers appears, by these rules, to be in
statistical control. No points are outside the control limits and there are no long runs of
points upwards or downwards or at either side of the central line.
Chart 2: Monitoring a HPLC Assay
To monitor the stability of a measurement system, a control sample may be measured
repeatedly over time, together with the test samples that are of primary interest. The
control sample results are then plotted in time order on a chart. The centre line for this
chart is the accepted correct value for the control material (typically the mean of recent
measurements on the material), and newly measured values for the control material are
expected to vary at random around the centre line. Sometimes the centre line might be
the certified value for a bought-in or a ‘house’ reference material.
UCL=95.519
95.5
%Potency
95.0
94.5
_
X=94.150
94.0
93.5
93.0
LCL=92.781
1
5
9
13
17
21
25
29
Observation
33
37
41
45
Figure 1.7.2 A control chart for the HPLC potency assay
Course Manual: PG Certificate in Statistics, TCD, Base Module
43
Figure 1.7.2 shows a control chart for a HPLC (high performance liquid
chromatography) potency assay of a pharmaceutical product [7]. The data displayed in
the chart were collected over a period of several months. At each time point two
replicate measurements were made on a control material, which was just a quantity of
material from one batch of the production material routinely manufactured and then
measured in the laboratory. These results were averaged and it is the average that is
plotted in the chart.
The average level of the measurement system to which Figure 1.7.2 refers appears, by
the AIAG rules, to be in statistical control. No points are outside the control limits and
there are no long runs of points upwards or downwards or on either side of the central
line. Accordingly, we can feel confident that the analytical system is stable and
producing trustworthy results.
Chart 3: Monitoring both Production and Analytical Systems
Figure 1.7.3 illustrates the benefits of having control charts in use for both production
results and analytical control data, when product reviews are carried out.
Figure 1.7.3(a) shows potencies for a series of batches of a drug with a clear downwards
shift in results. Such a shift suggests problems in the production system, but would
often lead to production management questioning the quality of the analytical results.
It has to be someone else’s fault!
Course Manual: PG Certificate in Statistics, TCD, Base Module
44
Figure 1.7.3: Simultaneous control charts for a production system (a) and the
analytical system (b) used to measure the potency of its product.
As shown in Figure 1.7.3(b), a stable control chart for the analytical system for the same
period is the best possible defence of the stability of the analytical results. If, on the
other hand, there had been a downward shift in the analytical system it would have
been reflected in Figure 1.7.3(b). Recognising such a shift would save much time that
would otherwise be wasted searching for a non-existent production problem. Thus, the
availability of control charts for both the production and analytical systems allows datadriven decision-making and can reduce inter-departmental friction when problems arise
at the interface7.
Chart 4: An Unstable Analytical System
7
In fact, the problem here could be due to changes in an in-coming raw material; so a third control
chart might well be worthwhile!
Course Manual: PG Certificate in Statistics, TCD, Base Module
45
Figure 1.7.4, represents 49 measurements on control samples made up to contain 50
parts per billion (ppb) of iron in pure water [7]. The sample was analysed by an
Inductively Coupled Plasma (ICP) Spectrometer over a period of months.
55
Fe Result
UCL=54.02
50
Mean=48.2
45
LCL=42.38
40
0
10
20
30
Run Number
40
50
Figure 1.7.4: A control chart for the iron (Fe) content of a water sample
(ppb)
The diagram shows an analytical system which is clearly out of control; in fact, three
gross outliers were removed before this chart was drawn. The data were collected
retrospectively from the laboratory records; the laboratory did not use control charts
routinely. They are presented here because they exhibit the classic features of an outof-control system: several points outside the control limits, a run of points above the
centre line and a run of points downwards. There is an obvious need to stabilise this
analytical system.
There are two ways in which control charts are used, viz., for assessing retrospectively
the performance of a system (as in Figure 1.7.4) and for maintaining the stability of a
system, which is their routine use once stability has been established. Where a chart is
being used to monitor a system we would not expect to see a pattern such as is exhibited
between observations 17 and 32 of Figure 1.7.4, where 16 points are all either on or
above the centre line. Use of a control chart should lead to the upward shift suggested
here being corrected before such a long sequence of out-of-control points could develop.
Course Manual: PG Certificate in Statistics, TCD, Base Module
46
Note that if the chart were being used for on-going control of the measurement process,
the centre line would be set at the reference value of 50 ppb. Here the interest was in
assessing the historical performance of the system, and so the data were allowed
determine the centre line of the chart.
The Theory Underlying the Control Limits
The centre line (CL) for the chart should be the mean value around which the
measurements are expected to vary at random. In a manufacturing context, this could
be the target value for the process parameter being measured, where there is a target,
but in most cases it is the mean of the most recent observations considered to be ‘incontrol’. Similarly, in a measurement context, the centre line will either be the mean of
recent measurements on the control material, or the accepted ‘true value’ for an inhouse standard or a certified reference material.
The control limits are usually placed three standard deviations above and below the
centre line, Figure 1.7.5(b); the standard deviation of individual measurements is used
if the points plotted are individual measurements, as in Chart 4, and the standard error
of the mean, if the plotted points are means of several measured values, as in Chart 1.
This choice may be based on the assumption that the frequency distribution of chance
causes will follow a Normal curve, or it may be regarded simply as a sensible rule of
thumb, without such an assumption. As we have seen a distribution curve can be
thought of as an idealised histogram: the area under the curve between any two values
on the horizontal axis gives the relative frequency with which observations occur
between these two values. Thus, as shown in Figure 1.7.5(a), 99.74% of the area under
any Normal curve lies within three standard deviations (3σ) of the long-run mean (μ)
and so, while the system remains in control, 99.7% of all plotted points would be
expected to fall within the control limits.
Where only single values are measured (as frequently happens in process industries, for
example) the control limits are:
Upper Control Limit (UCL) = CL + 3σ
Lower Control Limit (LCL) = CL – 3σ
where σ is the standard deviation of individual values.
If, as is more commonly the case in manufacturing of components, the point to be
plotted is the average of a number of values, say n, then an adjustment has to be made
to take account of the fact that means, rather than individual values, are being plotted.
If individual values give a frequency distribution, as shown in Figure 1.7.5(a), with
Course Manual: PG Certificate in Statistics, TCD, Base Module
47
mean μ and standard deviation σ, then a very large number of averages, each based on
n values from the same process, would give a similar frequency distribution centred on
μ but the width would be defined by σ/ n (the ‘standard error’). The distribution would
be tighter and more of the values would be close to μ. This simply quantifies the extent
to which the averaging process reduces variability, as discussed in Section 1.5: see
Figure 1.5.1, in particular.
Figure 1.7.5: Three sigma limits and a process shift
To obtain the correct control limits when plotting averages, we simply replace σ by
σ/ n in the expressions given above and obtain:
Upper Control Limit (UCL)
=
CL + 3 σ/ n
Lower Control Limit (LCL)
=
CL – 3 σ/ n
where σ is (as before) the standard deviation of individual values. The chart based on
single measurements is sometimes called an ‘Individuals or X-chart’ while the chart
based on means is called an ‘X-bar chart’; the two charts are, however, essentially the
same. Note that in a laboratory measurement context, where n is typically 2 or 3, the
Course Manual: PG Certificate in Statistics, TCD, Base Module
48
simplest and safest approach is to average the replicates and treat the resulting means
as individual values (see Mullins [7], Chapter 2).
The limits described above are known as ‘three sigma limits’, for obvious reasons; they
are also called ‘action limits’. They were first proposed by Shewhart in the 1920’s and
are almost universally used with this type of control chart. Their principal justification
is that if the process is in control then the probability of a point going outside the control
limits is very small: about three in a thousand. Accordingly, they give very few false
alarm signals. If a point does go outside the control limits it seems much more likely
that a problem has arisen (e.g., the process average has shifted upwards or downwards;
see Figure 1.7.5(c)) than that the process is stable, as in Figure 1.7.5(b), but the chance
causes have combined to give a highly improbable result. This is the rationale for the
first AIAG rule, quoted above.
The basis for the second AIAG rule (a run of seven points all above or all below the
central line) is that if the system is in control the probability that any one value is above
or below the central line is 1/2. Accordingly, the probability that seven in a row will be
at one side of the central line is (1/2)7=1/128; again, such an occurrence would suggest
that the process has shifted upwards or downwards. The third rule (a run of seven
points in a row that are consistently increasing (equal to or greater than the preceding
points) or consistently decreasing) has a similar rationale: if successive values are
varying at random about the centre line, we would not expect long runs in any one
direction.
The last catch-all rule (any other obviously non-random pattern) is one to be careful of:
the human eye is adept at finding patterns, even in random data. The advantage of
having clear-cut rules that do not allow for subjective judgement is that the same
decisions will be made, irrespective of who is using the chart. Having said this, if there
really is ‘obviously non-random’ behaviour in the chart (e.g., cycling of results between
day and night shift) it would be foolish to ignore it.
The assumption that the data follow a Normal frequency distribution is more critical for
charts based on individual values than for those based on averages. Averages, as we
saw in Section 1.5, tend to follow the Normal distribution unless the distribution of the
values on which they are based is highly skewed. In principle, this tendency holds when
the averages are based on very large numbers of observations, but in practice samples of
even four or five will often be well behaved in this regard. If there is any doubt
concerning the distribution of the measurements a Normal probability plot (see Section
1.3) may be used to check the assumption.
Course Manual: PG Certificate in Statistics, TCD, Base Module
49
Chart 5: A retail sales control chart
Stuart [11] considered the problem of monitoring cash variances in the till of a retail
outlet – a sports club bar. At the end of each day's trading, the cash in the till is
counted. The till is then set to compute the total cash entered through the keys, which
is printed on the till roll. The cash variance is the difference between cash and till roll
totals (note that ‘variance’ as used here is an accounting term, which is not the same as
the statistical use of the same word, i.e., the square of the standard deviation). Small
errors in giving change or in entering cash amounts on the till keys are inevitable in a
busy bar. Ideally, the cash variance will be zero. In the presence of inevitable chance
variation, the best that can be hoped for is that the cash variances will centre on zero.
In other words, the cash variance process is ideally expected to be a pure chance process
with a process mean of zero.
Sundays
20
12
V
a
4
r
i
-4
a
n - 12
c
e - 20
UC L
CL
LC L
10
20
30
40
50
We ek
Figure 1.7.6: Sunday cash variances control chart
A control chart covering Sunday cash variances for a year is shown in Figure 1.7.6. The
variances are recorded in pounds (the data pre-date the Euro). The centre line, is
placed at zero, the desired process mean. The control limits are placed at ±£12; the
limits were established using data from the previous year.
As may be seen from the chart, this process was well behaved, apart from three points
outside the control limits. For the first point, week 12, value £14.83, the large positive
cash variance indicates either too much cash having been put in the till or not enough
entered through the till keys. When the bar manager queried this, one of the bar
assistants admitted a vague recollection of possibly having given change out of £5
instead of out of £10 to a particular customer. The customer involved, when asked,
indicated that she had suspected an error, but had not been sure. The £5 was
reimbursed.
Course Manual: PG Certificate in Statistics, TCD, Base Module
50
In the second case, week 34, value –£22.08, an assistant bar manager who was on duty
that night paid a casual bar assistant £20 wages out of the till but did not follow the
standard procedure of crediting the till with the relevant amount.
The last case, week 51, value -£18.63, was unexplained at first. However, other out of
control negative cash variances on other nights of the week were observed, and these
continued into the following year. Suspicion rested on a recently employed casual bar
assistant. An investigation revealed that these cash variances occurred only when that
bar assistant was on duty and such a coincidence applied to no other member of staff.
The services of that bar assistant were ‘no longer required’ and the cash variances
returned to normal.
1.8 Conclusion
This chapter has introduced the concept of statistical variation – the fact that objects or
people selected from the same population or process give different numerical results
when measured on the same characteristic. It also showed that, where the same
object/person is measured repeatedly, different numerical results are obtained, due to
chance measurement error. In many cases, the variation between numerical results can
be described, at least approximately, by a Normal curve.
This curve will often describe the variation between means of repeated samples, also,
even where the raw data on which the means are based come from distributions that
are not themselves Normal. This fact is of great importance for what follows: the most
commonly used statistical procedures are based on means; therefore, statistical methods
based on Normal distributions will very often be applicable in their analysis. For this
reason, the properties of the Normal curve and its use in some simple situations (e.g.,
developing reference intervals in medicine, or use of control charts in industrial
manufacturing or in monitoring measurement systems) were discussed in the chapter.
References
[1]
[2]
[3]
[4]
Minitab Statistical Software, ( www.minitab.com )
Anderson, E., The irises of the Gaspé peninsula, Bulletin of the American Iris
Society 59, 2-5, 1935.
Fisher, R.A., The use of multiple measurements in taxonomic problems, Annals of
Eugenics 7, 179-188, 1936.
Bland, M., An Introduction to Medical Statistics, Oxford University Press, 2000.
Course Manual: PG Certificate in Statistics, TCD, Base Module
51
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
Strike, P.W. Measurement in Laboratory Medicine, Butterworth-Heinemann,
1996.
Hahn, G.J.and Meeker, W.Q., Statistical Intervals: a guide for practitioners, Wiley,
1991.
Mullins, E., Statistics for the Quality Control Chemistry Laboratory, Royal Society
of Chemistry, Cambridge, 2003.
Samuels, M.L., Statistics for the Life Sciences, Dellen Publishing Company, 1989.
Shewhart, W. A., Economic Control of the Quality of Manufactured Products,
Macmillan, London, 1931.
Montgomery, D.C., Introduction to Statistical Quality Control, Wiley, 2005
Stuart, M., An Introduction to Statistical Analysis for Business and Industry,
Hodder, 2003.
Chrysler Corporation, Ford Motor Company, and General Motors Corporation,
Statistical Process Control: Reference Manual, 1995.
Course Manual: PG Certificate in Statistics, TCD, Base Module
52
Outline Solutions
1.2.1.
(a)
A weight of 85 mg corresponds to a Z value of –2.14 as shown below – the standard Normal
table gives an area of 0.0162 to the left of –2.14, so the area to the left of 85 is also 0.0162.
z
x


85  100
 2.14
7
P(X < 85) = P(Z < -2.14) = P(Z>2.14) = 1 – P(Z < 2.14) = 1 – 0.9838 = 0.0162.
By symmetry, the area above 115 is also 0.0162.
Approximately, 1.6% of tablets will have weights either greater than 115 mg or less than
85 mg, which means that about 3.2% of tablets are outside these limits.
(b)
The calculations for part (b) are carried out in exactly the same way as those for (a).
Course Manual: PG Certificate in Statistics, TCD, Base Module
53
(c)
(i)
If we inspect the standard Normal table to find the value that has an area of 0.99 below it,
we find Z=2.33; therefore, -2.33 will have an area of 0.01 below it.
P(Z < -2.33) = 0.01
Z  2.33 
K  100
.
7
This means that K = 100 – 2.33(7) = 100 – 16.31 = 83.69
99% of tablets would be expected to weigh more than 83.69 mg.
(ii)
P(Z < 2.575) = 0.995 => P(Z >2.575) = 0.005
and, by symmetry, P(Z < –2.575) = 0.005
Z  2.575 
B  100
.
7
This means that B = 100 + 2.575(7) = 100 +18.025 = 118.025 mg
Course Manual: PG Certificate in Statistics, TCD, Base Module
54
By symmetry A = 100 – 2.575(7) = 100 –18.025 = 81.975 mg
1.2.2.
In the log10 scale we have a Normal distribution with mean 2.7423 and standard
deviation 0.1604.
(i)
Calculate the bounds (a, b) for the 95% reference interval in the log scale.
The reference bounds are: μ–1.96σ and μ+1.96σ which gives:
2.7423 ± 1.96(0.1604) or 2.4279 to 3.0567.
(ii)
Use your results to obtain the corresponding reference interval in the original
measurement scale: the bounds will be (10 a, 10b).
102.4279=267.9 and 103.0567=1139.5, so our reference interval in the original
measurement scale is 267.9 to 1139.5 (i.e., 268 to 1140 in practice). Note that
although the mean 2.7423 is the centre of the interval in the log scale, when we
back transform [102.7423=552.5], the corresponding value in the arithmetic scale is
not centred between the two bounds – the right-hand bound is much further
above 552.5 than the lower bound is below it. This reflects the skewed shape of
the original histogram. In fact, 552.5 is an estimate of the median (the steroid
value below which and above which 50% of the women lie). For a symmetrical
distribution the mean and the median coincide, but for right-skewed distributions
the mean will be higher; thus, the mean of the 100 original steroid values is 590.8
– the long tail pulls the mean upwards. Income distributions, for example, are
typically quite skewed, and the relatively small number of very high income
individuals increases the average income – the median value is, therefore, a
better one-number summary of a ‘typical’ member of the population.
Note also that the calculations above will be quite sensitive to the number of
decimal places used.
(iii)
What value, U, should be quoted such that only 1% of women from this
population would be expected to have a β-OHCS measurement which exceeds U?
Course Manual: PG Certificate in Statistics, TCD, Base Module
55
(note: curves are schematic and not to scale)
The critical value on the standard Normal curve which has 0.99 to the left and 0.01 to
the right is 2.33. From the relation:
z
x

it is clear that the corresponding value for a Normal curve with mean μ 2.7423 and
standard deviation σ = 0.1604 is μ+2.33σ=3.1160. Only 1% of the X=Log10(β-OHCS)
values would be expected to exceed X= Log10(U)=3.1160. The corresponding value in the
original measurement scale is U=103.1160= 1306.2.
1.3.1.
Follow the steps in the log10 scale we have a Normal distribution with mean 2.7423 and
standard deviation 0.1604.
The real data plot done in Excel (Minitab will be much better) displays that it is right skewed
while the line from means look cannot be differentiated from the straight line that arises with
Normal Data.
The effect of averaging is to produce a set of mean values whose distribution (their sampling
distribution) is approximately Normal – the application of the theoretical Central Limit Theorem
in practice on real data.
Course Manual: PG Certificate in Statistics, TCD, Base Module
56
Real
Data
x
Mean
V alues
Ranks
Fraction
Normal
Line
z
x
Ranks
-4
1
0.04
-1.77
-2.20
3
1
1
2
0.08
-1.43
-1.22
3.5
1
3
0.12
-1.20
-0.28
3.8
1
4
0.15
-1.02
0.46
1
5
0.19
-0.87
1
6
0.23
-0.74
2
7
0.27
2
8
2
9
3
Fraction
Normal
Line
z
0.05
-1.64
3.20
2
0.1
-1.28
3.91
3
0.15
-1.04
4.25
4
4
0.2
-0.84
4.53
1.09
4.5
5
0.25
-0.67
4.76
1.64
4.8
6
0.3
-0.52
4.97
-0.62
2.14
5
7
0.35
-0.39
5.17
0.31
-0.50
2.61
5.5
8
0.4
-0.25
5.35
0.35
-0.40
3.05
5.7
9
0.45
-0.13
5.53
10
0.38
-0.29
3.48
6
10
0.5
0.00
5.71
3
11
0.42
-0.19
3.89
6.1
11
0.55
0.13
5.88
3
12
0.46
-0.10
4.29
6.2
12
0.6
0.25
6.06
4
13
0.50
0.00
4.69
6.4
13
0.65
0.39
6.24
4
14
0.54
0.10
5.09
6.6
14
0.7
0.52
6.44
4
15
0.58
0.19
5.50
6.7
15
0.75
0.67
6.65
5
16
0.62
0.29
5.91
6.8
16
0.8
0.84
6.88
5
17
0.65
0.40
6.33
6.9
17
0.85
1.04
7.16
6
18
0.69
0.50
6.77
7.2
18
0.9
1.28
7.50
7
19
0.73
0.62
7.24
7.5
19
0.95
1.64
8.01
7
20
0.77
0.74
7.74
7.9
20
0.99
2.33
8.20
8
21
0.81
0.87
8.30
8
22
0.85
1.02
8.92
11
23
0.88
1.20
9.66
11
24
0.92
1.43
10.50
12
25
0.96
1.77
11.00
14
26
1.00
3.72
12.00
Course Manual: PG Certificate in Statistics, TCD, Base Module
57
Overlaid probability plot for random variable x1 and Mean values of x1-x20
1.4.1. We begin by finding the parameters for the doctorate completion time, T
μT = μL + μP + μD + μW = 30 + 10 + 120 + 16 = 176
2
𝜎𝑇2 = 𝜎𝐿2 + 𝜎𝑃2 + 𝜎𝐷2 + 𝜎𝑊
= 82 +32 +122 +32 =226
2
2
 T   L2   P2   D
 W
 15.03.
Since all four components of the total time are assumed to be Normally distributed, the
total time, T, will also have a Normal distribution.
Course Manual: PG Certificate in Statistics, TCD, Base Module
58
(i)
P(T < 3 years) = P(T < 156 weeks)
P(T  156)  P(Z 
T  T
T
)  P(Z 
156 176
)  P(T  1.33)  P(T  1.33)
15.03
 1  P(T  1.33)  0.09
The probability that the doctorate will take less than 3 years (156 weeks) is 0.09.
(ii)
P(T > 3.5 years) = P(T > 182 weeks)
P(T  182)  P( Z 
T  T
T
)  P( Z 
182  176
)  P(T  0.3992)
15.03
 1  P(T  0.40)  1  0.655  0.345
The chances of the postgraduate work taking more than three and a half years (182
weeks) are about 0.35.
Course Manual: PG Certificate in Statistics, TCD, Base Module
59
(iii)
Similarly, the probability that the work will take more than 4 years (208 weeks) is
about 0.02, as shown below.
P (T  208)  P ( Z 
T  T
T
)  P( Z 
208  176
)  P (T  2.13)
15.03
 1  P (T  2.13)  1  0.9834  0.0166
This example illustrates the analysis of project planning networks. Of course, the
current set of tasks is the simplest possible ‘network’ – a linear sequence of activities.
Real projects (consider for example the construction of an electricity generating
station) may involve thousands of activities, some of which may proceed
simultaneously (‘in parallel’), while others must be fully completed before others may
begin (e.g., foundations must be in place before walls can be built – these activities
are ‘in series’).
1.6.1.
(i)
A measurement of 101 corresponds to a Z value of 1.25 as shown below – the
standard Normal table gives an area of 0.8944 to the left of 1.25, so the area to the
right of 1.25 is 0.1056. The probability that a single measurement will exceed 101 is,
accordingly, 0.1056.
z
x


101  100
 1.25
0.8
P(X > 101) = P(Z>1.25) = 1 – P(Z < 1.25) = = 1 – 0.8944 = 0.1056
By symmetry, the probability that a single measurement will be less than 99 is also
0.1056. Hence, the probability that a single measurement will be more than one
unit from the true value is 2(0.1056) or 0.21.
The corresponding calculation for a divergence of 1.5 units shows a probability of
0.06.
(ii)
We saw in Section 1.5 that means are less variable than single measurements and,
specifically, that the variability of means is given by the standard error (the standard
deviation for single values divided by the square root of the number of values on
which the mean is based). To allow for the averaging in our calculations, therefore,
we simply replace the standard deviation by the standard error.
Course Manual: PG Certificate in Statistics, TCD, Base Module
60
The probability that a mean of two measurements will exceed 101 is given by:
z
x
/ n

101  100
0.8 / 2
 1.77
Where 𝑥 now represents the mean of two measurements.
P(𝑋̅> 101) = P(Z> 1.77)= 1 – P(Z < 1.77) = = 1 – 0.9616 = 0.0384
By symmetry, the probability that the mean of two measurement will be less than 99
is also 0.0384. Hence, the probability that the mean of two measurements will be
more than one unit from the true value is 2(0.0384) or 0.08.
The value of making even two measurements instead of one is clear – the probability
of an error of one unit has been reduced from 0.21 to 0.08.
The corresponding probability for the mean of three measurements is 0.03.
1.6.2.
(i)
A trawl through the website HorsesForum.com suggests that a nailed-on steel
horseshoe will last about 5 to 8 weeks before it needs to be re-set. Assuming the
lifetime of a horseshoe is normally distributed with population mean μ = 7 weeks
and standard deviation σ = 1.25 weeks what is the probability that a nailed-on
horseshoe picked at random from the population will last 9 or more weeks before
needing re-set.

Compute z-value based on x = 9:
𝑧=

𝑥−𝜇
𝜎
9−7
= 1.25 = 1.6
Compute probability
𝑥−𝜇
𝑃(𝑥 ≥ 9) = 1 − 𝑃(𝑥 < 9) = 1 − 𝑃 ( 𝑧 <
)
= 1−𝑃(
9−7
1.25
𝜎
) = 1 − 𝑃(1.6) = 1 − 0.945 =0.055
The probability the nailed-on horseshoe last 9 or more weeks is 0.055 or
just over a 1-in-20 chance.
(ii)
A second website ‘The Chronicle of the Horse’ advises so-called ‘glued-on’
horseshoes, that is shoes that are glued rather than nailed-on, may be used in
cases of laminitis (aka white line disease in USA) where the hoof is unable to
accommodate nails. Gleaning the posts on the website seems to indicate that the
population mean lifetime of glued-on shoes is μ = 5 weeks with standard
deviation σ = 2.0 weeks. Assuming the lifetimes are normally distributed what is
the probability that a glued-on horseshoe picked at random from the population
will last 9 or more weeks before needing re-set.
Course Manual: PG Certificate in Statistics, TCD, Base Module
61

Compute z-value based on x = 9:
𝑧=

𝑥−𝜇
𝜎
=
9−5
2.0
=2
Compute probability
𝑥−𝜇
𝑃(𝑥 ≥ 9) = 1 − 𝑃(𝑥 < 9) = 1 − 𝑃 ( 𝑧 <
)
= 1−𝑃(
9−5
2.0
𝜎
) = 1 − 𝑃(2) = 1 − 0.977 =0.023
The probability the glued-on horseshoe last 9 or more weeks is 0.023 or
just under a 1-in-40 chance.
(iii)
Comparing the information from the two websites: What is the probability that a
nailed-on horseshoe will last longer than a glued-on horseshoe, i.e the difference
between the lifetimes of the two types of horseshoe is greater than zero.

We want to know whether the difference between nailed-on and glued-on
horseshoe lifetimes is greater than zero based on population means obtained
by ‘received wisdom’ only.
Compute difference in population means 𝝁
𝑑 = 𝜇𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 − 𝜇𝐺𝑙𝑢𝑒𝑑−𝑜𝑛 = 7 − 5 = 2.

Compute the std err of difference
2
2
𝑆𝐸(𝑑) = 𝑆𝐸(𝑥𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 − 𝑥𝐺𝑙𝑢𝑒𝑑−𝑜𝑛 ) = √ 𝜎𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛
+ 𝜎𝐺𝑙𝑢𝑒𝑑−𝑜𝑛
= √1.252 + 22 = √5.5625
= 2.36
𝑃(𝑑 > 0) = 1 − 𝑃(𝑑 ≤ 0) = 1 − 𝑃 ( 𝑧 <
= 1−𝑃(
0−2
2.36
0−𝑑
𝑆𝐸(𝑑)
)
) = 1 − 𝑃(−0.847) = 1 − 0.2 =0.8
The probability that a single random nailed-on horseshoe will last longer
than another single random glued-on horseshoe is 0.2 or a 4-in-5 chance.
(iv)
Comparing a sample mean to a population value μ (e.g population mean):
The website data used in part (i) was in fact based on a sample of n=5 with
𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 = 7. On the basis of this sample data what is the probability that the
mean lifetime μ for (the population of) nailed-on horseshoes is at least (μ =) 9
weeks.

We want to know how far the ‘actual’ sample mean computed from the
observed data values only is from the value of μ = 9 weeks.
Course Manual: PG Certificate in Statistics, TCD, Base Module
62

Compute the std err of the mean
Note: because we are dealing with samples and the variance of a sample
mean is 𝜎 2 /𝑛
𝑆𝐸(𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 ) = √
2
𝜎𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛
1.252
=√
= 0.559
𝑛𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛
5
𝑃(𝜇 > 𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 ) = 1 − 𝑃(𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 ≤ 𝜇) = 1 − 𝑃 ( 𝑧 <
= 1−𝑃(𝑧 <
𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛−𝜇
𝑆𝐸(𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛)
7−9
)
𝑆𝐸(𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 )
7−9
) = 1−𝑃(𝑧 <
0.559
)
−2
= 1−𝑃(
) = 1 − 𝑃(−3.58) = 1 − 0.998 = 0002
0.559
So, the chances that the unknown population mean lifetime of nailed-on
horseshoes lasting 9 or more weeks is about 1-in-5000 based on the
sample.
Note: this is a statement about mean values and not about the sample
values themselves. In this case μ = 9 weeks can be thought of as a
hypothesised value for the unknown population mean.
Chapter 2 will take up this idea of hypothesis testing in more detail.
(v)
Exam style question:
Comparing the information based on samples from the two websites: The website
data used in part (i) was in fact based on a sample of n=5 with 𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 = 7
while in part (ii) the sample size was n=2 and 𝑥̅𝐺𝑙𝑢𝑒𝑑−𝑜𝑛 = 5. On the basis of these
sample sizes what is the probability that a nailed-on horseshoe will last longer
than a glued-on horseshoe, i.e the difference between the means of the lifetimes of
the two types of horseshoe is greater than zero.

We want to know whether the difference between nailed-on and glued-on
horseshoe lifetimes is greater than zero based on ‘actual’ sample means
computed from the observed data values only.
̅
Compute difference in sample means 𝒙
𝑑̅ = 𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 − 𝑥̅𝐺𝑙𝑢𝑒𝑑−𝑜𝑛 = 7 − 5 = 2.

Compute the std err of this difference
Course Manual: PG Certificate in Statistics, TCD, Base Module
63
Note: because we are dealing with samples and the variance of a sample
mean is 𝜎 2 /𝑛 we have to use this quantity in our usual formula for adding
two or more variances as follows
2
2
𝜎𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛
𝜎𝐺𝑙𝑢𝑒𝑑−𝑜𝑛
𝑆𝐸(𝑑̅ ) = 𝑆𝐸(𝑥̅𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 − 𝑥̅𝐺𝑙𝑢𝑒𝑑−𝑜𝑛 ) = √
+
𝑛𝑁𝑎𝑖𝑙𝑒𝑑−𝑜𝑛 𝑛𝐺𝑙𝑢𝑒𝑑−𝑜𝑛
=√
1.252 22
+
= √0.3125 + 2 = 1.52
5
2
𝑃(𝑑 > 0) = 1 − 𝑃(𝑑 ≤ 0) = 1 − 𝑃 ( 𝑧 <
= 1−𝑃(
2−0
1.52
𝑑−0
)
𝑆𝐸(𝑑̅ )
) = 1 − 𝑃(1.32) = 1 − 0.907 =0.093
The probability that an average nailed-on horseshoe will last longer than
an average glued-on horseshoe is 0.093 or just under a chance of 1-in-10.
So, based on our sample information the chance of an average nailed on
horseshoe lasting longer than an average glued-on shoe compared to a
single random nailed on horseshoe lasting longer than a single random
glued-on shoe has halved.
The distinction between making comparison between individual cases
and comparison based on sample mean cannot be overemphasised.
We gain precision using sample information.
1.6.3.
Combining data - Meta-analysis study
(i)
In a 3-rd world country in Latin America a study shows that infants born to
families who cook on an open Wood stove have an average birth weight of μ = 2.9
kg with standard deviation 𝜎 = 0.5kg.
What is the probability that an infant born to one of these families is over 3.6kg?

Compute z-value based on x = 3.6:
𝑧=

𝑥−𝜇
𝜎
=
3.6−2.9
0.5
= 1.6
Compute probability
𝑥−𝜇
𝑃(𝑥 ≥ 3.6) = 1 − 𝑃(𝑥 < 3.6) = 1 − 𝑃 ( 𝑧 <
)
= 1−𝑃(
3.6−2.9
0.5
𝜎
) = 1 − 𝑃(1.4) = 1 − 0.919 =0.081
The probability that the weight of an infant in a family that cooks on a
wooden stove is greater 3.6kg is 0.08 or just under a 1-in-12 chance.
Course Manual: PG Certificate in Statistics, TCD, Base Module
64
(ii)
Cooking in the country is also done an open fires and electric cookers in this
country. The respective average birth weight statistics are μ = 2.8kg and 3.1kg
while the standard deviations are 0.4kg and 1.3kg respectively.
Repeat part (i) for an electric stove.

Compute z-value based on x = 3.6:
𝑧=

𝑥−𝜇
𝜎
3.6−3.1
1.3
= 0.38
Compute probability
𝑥−𝜇
𝑃(𝑥 ≥ 3.6) = 1 − 𝑃(𝑥 < 3.6) = 1 − 𝑃 ( 𝑧 <
)
= 1−𝑃(
(iii)
=
3.6−3.1
1.3
𝜎
) = 1 − 𝑃(0.38) = 1 − 0.648 =0.352
The probability that the weight of an infant in a family that cooks on an
electric stove is greater 3.6kg is 0.35 or just over a 1-in-3 chance.
Combining the information on cooking types: What is the probability that an
infant born in this country will be less than 2.3kg.

So we want to combine the information from 3 studies to see whether a child
born in the country is likely to have a small birth weight based on population
means obtained by ‘received wisdom’ only.
Compute the overall population mean 𝝁
𝜇 = ( 𝜇𝑤𝑜𝑜𝑑 + 𝜇𝑜𝑝𝑒𝑛 + 𝜇𝑒𝑙𝑒𝑐𝑡𝑟𝑖𝑐 )/3 = (2.9 + 2.8 + 3.1)/3 = 2.93

Compute the std err of the overall population mean
2
2
2
𝑆𝐸(𝜇) = √ (𝜎𝑤𝑜𝑜𝑑
+ 𝜎𝑜𝑝𝑒𝑛
+ 𝜎𝑒𝑙𝑒𝑐𝑡𝑟𝑖𝑐
)/3 = √(0.52 + 0.42 + 1.32 /3) = √2.1/3 = 0.84
𝑃(𝑥 < 2.3) = 𝑃 ( 𝑧 <
= 𝑃(
2.3−2.93
0.84
𝑥−𝜇
)
𝑆𝐸(𝜇)
) = 𝑃(−0.75) =0.227
The probability that the weight of a random infant in the population in
this country is less than 2.3kg is 0.23 or a 1-in-4 chance.
(iv)
Combining the information on cooking types based on samples from the three
cooking type studies: The study data used in parts (i) and (ii) was in fact based on
3 samples each of size n=36 (108 in all). Taking the sample mean in each case to
be the population mean (i.e. with 𝑥̅ = 𝜇) repeat part (iii) above and comment.

So we want to combine the information from 3 studies to see whether the
average birth weight of child born in the country is likely to be under 2.3kg.
Note the important distinction, here we are looking at the average birth
weight of infant in the population not the weight of any random infant in the
population as in part (iii).
Course Manual: PG Certificate in Statistics, TCD, Base Module
65
̅
Compute overall sample means 𝒙
This is exactly same as in part (iii) but with different notation
𝑥̅ = ( 𝑥̅𝑤𝑜𝑜𝑑 + 𝑥̅𝑜𝑝𝑒𝑛 + 𝑥̅𝑒𝑙𝑒𝑐𝑡𝑟𝑖𝑐 )/3 = (2.9 + 2.8 + 3.1)/3 = 2.93

Compute the std err of the overall sample mean
As in previous question, because we are dealing with samples and the
variance of a sample mean is 𝜎 2 /𝑛 we have to use this quantity in our usual
formula for adding two or more variances as follows
𝑆𝐸(𝑥̅ ) = √(
= √(
2
2
2
𝜎𝑜𝑝𝑒𝑛
𝜎𝑤𝑜𝑜𝑑
𝜎𝑒𝑙𝑒𝑐𝑡𝑟𝑖𝑐
+
+
) /3
𝑛𝑤𝑜𝑜𝑑 𝑛𝑜𝑝𝑒𝑛 𝑛𝑒𝑙𝑒𝑐𝑡𝑟𝑖𝑐
0.52 0.42 1.32
+
+
) /3 = √(0.007 + 0.004 + 0.045)/3 = 0.137
36
36
36
𝑃(𝑥̅ < 2.3) = 𝑃 ( 𝑧 <
= 𝑃(
2.3−2.93
0.137
𝑥̅ −𝜇
)
𝑆𝐸(𝑥̅ )
) = 𝑃(−4.59) =0.00001
The probability that the average birth weight of an infant in a family in this
country is less than 2.3kg is 0.004 or a 1-in-100,000 chance.
So, based on our sample information the chance of a child being born with
an ‘average’ weight below 2.3kg is over 25,000 times less than that of any
random infant in the population being born below 2.3kg.
Clearly, statements about the ‘mean’ are very different to similar
sounding statements about particular cases.
Course Manual: PG Certificate in Statistics, TCD, Base Module
66