Download Handout-4

Handout-4
Course 201N
1st Semester 2006-2007
Inorganic Chemistry
Instructor: Jitendra K. Bera
Contents
2. Bonding in Transition metal Complexes
Valence Bond Theory
Crystal Field Theory
Octahedral field and CFSE
Tetrahedral field
Tetragonal Symmetry: Square Planar Complexes
Factors affecting the magnitude of ∆
Thermodynamic aspects of the CFSE
Lattice energy and Site Preferences in Spinels
Distortions in Octahedral geometry
Bonding in Metal Complexes
Valence Bond Theory
This theory was developed by Pauling. The model utilizes
hybridization of metal valence orbitals to account for the observed
structures and magnetic properties of complexes. Pauling
suggested that (n-1)d, ns and np undergo hybridization to give
hybridized orbitals. An empty hybrid orbital on the metal center
can accept a pair of electrons from a ligand to form a σ-bond.
Example: Octahedral complex of Co(III)
The atomic orbitals required for an octahedral complex are
the 3dz2, 3dx2–y2, 4s, 4px, 4py, and 4pz
These orbitals must be unoccupied so as to be available to
accept six pairs of electrons from the ligands
3d
4s
4p
d2sp3
Common geometries and corresponding hybridization Schemes
C.N.
2
3
4
5
4
5
6
6
Geometry
Linear
Trigonal planar
Tetrahedral
Square planar
Trigonal bipyramidal
Square-based pyramidal
Octahedral
Trigonal prismatic
Orbitals
s, pz
s, px, py
s, px, py, pz
s, px, py, dx2-y2
s, px, py, pz, dz2
s, px, py, pz, dx2-y2
s, px, py, pz, dz2, dx2-y2
s, dxy, dyz, dxz, dz2, dx2-y2
Description
sp
sp2
sp3
sp2d
sp3d
sp3d
sp3d2
sd5
Examples
[Ag(NH3)2]+
[HgI3]–
[FeBr4]2–
[Ni(CN)4]2–
[CuCl5]3–
[Ni(CN)5]3–
[Co(NH3)6]3+
[Mo(S2C2Ph2)3]
Example: The complex [PtCl4]2- is diamagnetic, where as [NiCl4]2- is paramagnetic with
two unpaired electrons. VBT proposes the use of dsp2 hybridization for Pt (to afford a
square-planar geometry around it) and the use sp3 hybridization for Ni2+(to afford a
tetrahedral geometry).
[PtCl4]2-
5d
6s
6p
dsp2
[NiCl4]2-
3d
4s
4p
sp3
HW: The octahedral complexes, [CoF6]3- is known to be paramagnetic with two
unpaired electrons. In contrast, the compound [Co(NH3)6]3+ is diamagnetic.
Suggest the hybridization schemes.
Limitations:
Most transition metal complexes are colored, but the theory does not provide any
explanation
The VBT does account for the observed magnetic moment in complexes.
However, orbitals of higher energy have to be utilized (quite arbitrarily) for cases
as in [CoF6]3- where 4s, 4p and 4d orbitals are utilized in the sp3d2 hybridization.
The VBT does not explain the temperature dependent magnetic properties
Crystal Field Theory
In view of the above weaknesses, an alternative bonding model was applied to transition
metal complexes. This is known as crystal field theory (CFT). It has been originally
proposed by Hans Bethe and van Vleck in 1929. The assumptions of the crystal field
theory are as follows:
The interaction between the metal ion and the ligand is assumed to be purely
electrostatic (ionic) in nature.
The ligands are treated as point charges. Consequent to this assumption, the CFT
does not allow for any overlap between the metal orbitals and the ligand orbitals.
In spite of the above unrealistic premise, the CFT has been remarkably successful in
explaining many properties of the transition metal complexes. This is mainly due to the
fact that the symmetry considerations involved in the crystal field approach are identical
to the more sophisticated molecular orbital theory that we will consider later.
[Ti(OH2)6]3+
octahedral
d1 ion
violet
paramagnetic
[Fe(OH2)6]2+
octahedral
d6 ion
green-blue
paramagnetic
magnetic
behaviour
colour
[Co(NH3)6]3+
octahedral
d6 ion
yellow
diamagnetic
stability of ox. states
Crystal Field Theory
lattice energies
[Cu(OH2)6]2+
distorted octahedral
d9 ion
blue
paramagnetic
hydration
enthalpies
structures
[Ni(CN)4]2square planar
d8 ion
yellow
diamagnetic
[ZnCl4]2tetrahedral
d10 ion
colourless
diamagnetic
Consequences of the metal ion interaction with ligands
The five d orbitals in an isolated, gaseous metal ion are degenerate (are of the
same energy and symmetry).
If a spherically symmetric field of negative charges is placed around the metal ion
the orbitals will remain degenerate, but all of them will be raised in energy as a
result of repulsion between the negative field and the metal electrons in the
orbitals.
If the field results produced by the ligands is not spherically symmetric but of a
particular symmetry (octahedral, tetrahedral etc), the d-orbitals are not affected
equally and the degeneracy of the d orbitals is removed.
E
degenerate d-orbitals
free ion
degenerate d-orbitals
spherical charge distribution around metal ions
Shapes of d-Orbitals
Note: There are six wave functions that can be written for these orbitals. The orbital dz2
orbital is regarded as a linear combination of the dz2-y2 and dz2-x2. The dz2 and dx2-y2
orbitals are along the axis, dxy, dxz, dyz orbitals are in-between the axis
Octahedral Field
An octahedral field is described by six ligands at the six corners of an octahedron and the
metal is at the center. Hence, the orbitals lying along the axes (dz2 and dx2-y2) will be more
strongly repelled than those whose orbitals are lying in
between the axes (dxz, dyz, dxy). Thus, the overall consequence
is that the degenerate set of five orbitals is now split into two
sets, one at a higher energy and one at a lower energy. The
higher energy set of orbitals (dz2 and dx2-y2 are labeled as eg
and the lower energy set is labeled as t2g). The energy
separation between the two levels is denoted by ∆o or 10 Dq.
Note that moving from a hypothetical spherical field to an
octahedral field does not alter the average energy of the five
d orbitals. The weighted mean of these two sets of perturbed
orbitals is taken as zero: this is also known as ‘barycenter’. To
maintain the average energy, the eg orbitals need to be repelled by an amount of 0.6 ∆o
and the t2g orbitals to be stabilized to the extent of 0.4 ∆o with respect to the barycenter.
Splitting of d-orbitals in an Octahedral field
L
L
L
L
L
L
eg
3/5 ∆Ο
∆Ο =10 dq
2/5 ∆Ο
ion in an spherical field
t2g
ion in an octahedral ligand field
Representation of Symmetry Point Groups: Mulliken labels
A - symmetric w.r.t. the highest order axis Cn
B - antisymmetric
One- (A or B), Two- (E), Three- (T)
dimensional representation
Symmetric (') or antisymmetric (") w.r.t. σh
A'1g
Presence (g) or absence (u) a center of inversion
Symmetric (1) or antisymmetric (2) w.r.t. a second symmetry element C2 or σv
The splitting energy ∆Ο can be determined from spectroscopic data. Let us consider the
case of [Ti(H2O)6]3+. This compound is purple in color. Unlike Valence Bond theory, the
crystal field treatment explains the color. The lone d electron (Ti3+ is a d1 species) in an
octahderal crystal field enters the lower energy orbitals to have a ground state electronic
configuration, t2g1eg0. The purple color is the result of the absorption of light and the
excitation of the electron to the higher energy eg level (t2g1eg0 → t2g0eg1). This excitation
corresponds to 20,300
cm-1 corresponding to an
energy of absorption of
243 kJ mol-1. This
corresponds to ∆o in this
molecule. It should be
mentioned here that the d1
is the simplest case in that
the
transition
from
1 0
0 1
t2g eg → t2g eg reflects
the
actual
energy
difference between the t2g
and eg levels. For multielectron system such as (d2, d3 etc), electron-electron interactions make the calculations
more complicated.
[Note: The absorption spectrum of [Ti(H2O)6]3+ appears broad with a shoulder present.
We will explain this later.]
HW. The UV-Vis spectrum of ReF6 exhibits absorption at 32,500 cm-1. Calculate
∆o in kJ mol-1.
Crystal Field Stabilization Energy (CFSE)
d1, d2 and d3: For these electronic configurations the only possible arrangements in the
octahedral crystal field are t2g1eg0, t2g2eg0and t2g3eg0 respectively. The stabilization energy
for these configurations therefore are 0.4∆o, 0.8∆o and 1.2∆o respectively.
d4-d7: For the d4 configuration, however, there are two possibilities t2g4eg0 or t2g3eg1. Two
competing factors determine which configuration is preferred. In order to force an
electron to pair with another an energy called Pairing energy (P) has to be invested. This
is made up of two terms. One: the Coulombic repulsion arising out of forcing two
electrons to occupying the same orbital. Two: the loss of exchange energy that occurs as
electrons with parallel spins are forced to have anti-parallel spins. If P> ∆o the
configuration t2g3eg1 is preferred. This is known as weak field or high spin situation. If
∆o>P the configuration t2g4eg0 is adopted. This leads to strong field or low spin situation.
The reason for the nomenclature high and low spin arises from the magnetic moment
differences between the two configurations. Thus, t2g4eg0, has only two unpaired electrons
and therefore would have a magnetic moment of 2.83 BM. In contrast the configuration
t2g3eg1 would have four unpaired electrons with a magnetic moment of 4.90 BM.
d8-d10: For these electronic configurations the only possible arrangements in the
octahedral crystal field are t2g6eg2, t2g6eg3and t2g6eg4 respectively. The stabilization energy
for these configurations therefore are 1.2∆o, 0.6∆o and 0.0∆o respectively.
A simplified table showing the CFSE’s and the number of unpaired electrons for various
configurations under both strong and weak field situations is shown below. This table
neglects the pairing energy contribution.
Tetrahedral Symmetry
Consider the metal ion along with its d orbitals in the center of the cube. Arrange the
ligands alternately in four corners of the cube. This arrangement would keep two ligands
in the top face of the cube and two in the bottom face. Notice that in this arrangement
none of the ligands approach the metal along
Splitting of d-orbitals in an Tetrahedral field
the Cartesian coordinate axes. Consequently
the orbitals lying along the axes (dz2 and dx22
L
y ) will be less strongly repelled than those
L
whose orbitals are lying in between the
axes(dxz, dyz, dxy). Thus, the overall
consequence is that the previously degenerate
L
L
set of five orbitals is now split into two sets,
t2
one at a higher energy and one at a lower
2/5 ∆t energy. The higher energy set of orbitals (dxz,
dyz, dxy) are labeled as t2 and the lower energy
set (dz2 and dx2-y2) is labeled as e. [The
subscripts ‘g’ disappear here since the
ion in an spherical field
3/5 ∆t
tetrahedron lacks a center of inversion]. The
energy separation between the two levels is
e
denoted by ∆t or 10 Dq.
ion in an tetrahedral ligand field
The crystal field splitting in the tetrahedral field is intrinsically smaller than in the
octahedral field because a) There are only four ligands surrounding the metal ion and b)
none of them have a direct effect on the d orbitals. For most purposes the relation ship
between the two crystal field separation energies may be represented as ∆t = 4/9∆o.
When to expect Tetrahedral geometry?
Ligands are large, less ligand-ligand repulsion
metal ions with zero CFSE (d0, d5, d10) or small CFSE (d2 and d7).
Examples: MnO4- (d0), FeCl4- (d5, h.s.), CoCl42- (d7, h.s.), ZnCl42- (d10)
Note: Having fewer number of ligands (four) and they are not aligned along the orbital
axis, the CFSE in most cases are too small to overcome the spin pairing energy, therefore,
tetrahedral low-spin complexes are rare. A rare example is Cr[N(SiMe3)2]3[NO].
NO
Si
L=
Cr
L
L
L
N
Si
Tetragonal Symmetry: Square Planar Complexes
If two trans ligands in an octahedral ML6 complex (consider those along the z-axis) are
moved either towards or away from the metal ion, the resulting is said to be tetragonally
distorted. Ordinarily such distortions are not favored since they result in a net loss of
bonding energy. In certain situations, however, such a distortion is favored because of a
Jahn-Teller effect (we will study this later in details). A complex of general formula
trans-MA2B4 also will have tetragonal symmetry. For now, we will consider the limiting
case of tetragonal elongation, a square planar ML4 complex, for the purpose of deriving
its d-orbital splitting pattern.
The crystal field diagram for the tetragonally distorted complex and the square-planar
complexes is shown below. Removal of ligands from z-direction completely leads to the
square-planar geometry. This geometry is favored by metal ions having a d8
configuration in the presence of a strong field. This combination gives low-spin
complexes where the first four orbitals are occupied and the high-energy dx2-y2 orbital is
unoccupied.
When to expect Square Planar geometry?
In the case of Ni2+(a first row transition metal ion with a d8 electronic
configuration) a strong field ligand such as CN- is required to effect a squareplanar complex formation. Example: [Ni(CN)4]2 With a second row d8 metal ion such as Pd2+( which already generates a strong
field) even a weak field ligand such as Cl- leads to the formation of a squareplanar complex, for example, [PdCl4]2-.
Factors affecting the magnitude of ∆
1. Higher oxidation states of the metal atom correspond to larger ∆ :
∆ =10,200 cm-1 for [CoII(NH3)6]2+ and 22,870 cm-1 for [CoIII(NH3)6]3+
∆ =32,200 cm-1 for [FeII(CN)6]4- and 35,000 cm-1 for [FeIII(CN)6]3-
2. In groups heavier analogues have larger ∆. For hexaammine complexes [MIII(NH3)6]3+:
∆ = 22,870 cm-1 (Co)
34,100 cm-1 (Rh)
41,200 cm-1 (Ir)
3. Geometry of the metal coordination unit affects ∆ greatly. For example, tetrahedral
complexes ML4 have smaller ∆ than octahedral ones ML6:
∆ = 10,200 cm-1 for [CoII(NH3)6]2+
5,900 cm-1 for [CoII(NH3)4]2+
4. Ligands can be arranged in a spectrochemical series according to their ability to
increase ∆ at a given metal center:
I- < Br- < Cl- < F- , OH< H2 O
< NH3 < NO2- < Me- < CN- < CO
For [CoIIIL6] we have ∆, cm-1: 13,100 (F-),
20,760 (H2O),
22,870 (NH3)
For [CrIIIL6] we have ∆, cm-1: 15,060 (F-),
17,400 (H2O),
26,600 (CN-)
Note: H2O > HO-; this can’t be explained based on electrostatic model of CFT. We shall
discuss in M.O. theory later.
Thermodynamic aspects of the CFSE
Lattice Energy, Enthalpy of hydration and ionic radii. The plot of CFSE with the delectron counts of the metal ions follows a double-hump as shown below. The CFSE is
zero for ions with d0 and d10 configurations in both strong and weak ligand fields. The
CFSE is also zero for d5 configuration in a weak field. All other arrangements have some
CFSE which increases the
thermodynamic stability of the
complexes. The CFSE is
manifested
in
the
thermodynamic data of the
complexes.
Let us start to look at the lattice energies of divalent metal halides starting from Ca2+ and
proceed to Zn2+. All of these have octahedral crystal fields in which the metal is
surrounded by six halide ions. Lattice energy is the energy released when ions come
together from infinite separation to form a crystal and can be estimated with reasonable
accuracy using the Born-Landé equation. The measured and calculated values for the
main
group
elements (which
have no CFSE)
are
in
close
agreement.
In
contrast,
many
transition
metal
compounds have
higher measured
lattice
energies
than the calculated
values. A plot of the lattice energies of the halides of the first row transition elements in
the divalent state is given in figure below. The ions Ca2+, Mn2+ and Zn2+ lie on a straight
line. These do not possess any CFSE (Mn2+ and Zn2+ are d5 and d10). The deviations from
the straight line occur for situations where CFSE contributions are present. The heights of
other points above the broken line correspond to the CFSEs. Values obtained in this
method agree with those obtained by spectroscopy.
In addition to the lattice energy, the enthalpies of hydrations for divalent and trivalent
transition metal ions and the ionic radii of divalent transition metal ions exhibit similar
double-humped curves illustrating the effects of CFSE.
Site Preferences in Spinels. Spinels have the formula AB2O4 where A is a Group 2
metal ion or a transition metal ion in an oxidation state of +2. B is a Group 3 metal ion or
a transition metal ion in an oxidation state of +3. The oxide ions act as ligands (weak
field ligands) and are arranged in a close packed arrangement. The divalent metal ions
have a coordination number of four and the trivalent metal ions have a coordination
number of six (These occupy the tetrahedral and octahedral voids present in the close
packed arrangement of the oxide ions). In a normal spinel such as MgAl2O4 the
magnesium ions have a tetrahedral geometry and the octahedral geometry is preferred by
the aluminum ions. In some situations an inverted structure is obtained and there is
reason to believe that this occurs because of CFSE. Take the example of NiFe2O4. Ni2+ is
a d8 system while Fe3+ is a d5 system. For the latter the CFSE is zero whether it adopts a
tetrahedral (e2t23) or an octahedral( t2g3eg2) geometry. However, for Ni2+ it is
advantageous to adopt an octahedral geometry from a CFSE point of view. Let us
compute the energies and quantify this. In a tetrahedral environment (e4t24) the CFSE is
0.8 ∆t. In octahedral units this is about 0.4∆o (recalling that ∆t is about half as much as
∆o). If Ni2+ is present in an octahedral geometry its CFSE energy is1.2 ∆o. Therefore,
there is an advantage for the Ni2+ ion (known as octahedral site stabilization energy or
OSSE) to exchange places with Fe3+. Consequently an inverted spinel structure is formed
which can be written as (Fe3+)(Ni2+Fe3+)O4. In this structure half of the Fe3+ ions occupy
the tetrahedral voids and the other half occupy the octahedral voids. All the Ni2+ occupy
the octahedral voids. Note: Although the CFSE contribution to the total bonding energy
of a system is only 5-10%, it may be the deciding factor when the other contributions are
reasonably constants.
HW. Explain the normal spinel structure for Mn3O4 and inverse spinel
structure for Fe3O4.
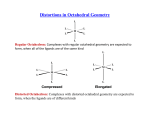
Distortions in Octahedral geometry
The Jahn-Teller Theorem was published in 1937 and states: For a non-linear molecule in
an electronically degenerate state, distortion must occur to lower the symmetry, remove
the degeneracy and lower the energy. Before moving further, the term ‘electronically
degenerate state’ require further elaboration. Consider Ti3+ present in an octahedral
environment. It is a d1 system and the lone electron has the possibility of occupying any
of the three d orbitals. Three electronic configurations are possible depending on which
orbital is occupied (dxz1, dxy0, dyz0), ( dxz0, dxy1, dyz0) and ( dxz0, dxy0, dyz1). Such a situation
is called an electronically degenerate state. Similarly, for Cr3+, that is d3 system, there is
only one way to fill the t2g orbitals (dxz1, dxy1, dyz1) and hence it is an example of
electronically non-degenerate state. The Jahn-Teller theorem predicts that a non-linear
molecule that has an electronically degenerate state, distortion occurs so that the
degeneracy is removed, the consequence is that the symmetry of the molecule is lowered
and the system becomes more stable by loosing energy. We will consider two types of
distortions to be operating, z-in and z-out.
In the case of octahedral complexes the tetragonal distortion reduces octahedral (Oh)
symmetry of a complex to tetragonal (D4h) structures producing either elongated (2-long,
4-short) or compressed (4-long, 2-short) tetragonal bipyramid structures. Consider a case
of [Ti(OH2)6]3+, a d1 system. To remove the electronic degeneracy, the t2g orbital is split,
the energy of dxz and dyz orbitals are raised in energy while the dxy orbital is lowered. The
separation lets say δ2. In the eg set the dz2 orbital is raised in energy in comparison to the
dx2-y2 and the separation is δ1. In this way, the lone electron is on the dxy orbital and the
electronic degeneracy has been removed. The repulsion experienced in the orbitals
containing the x,y component is more than the orbitals contain the z-component. The
consequence of this is that four long (along x, y axis) and one short (along z axis) bonds.
This is known as Z-in case.
Consider the case of Cu(II), the d9 system. The t2g set is split, the dxz and the dyz orbitals
are lowered in energy while the dxy orbital is raised. In the eg set, the dz2 orbital is
lowered in energy in comparison to the dx2- y2. The odd electron resides in dx2- y2 and the
degeneracy in the system is
NH3
F
removed. The consequence
2+
3is that the four short (along
2.62
2.09
x, y axis) and one long
H3N
NH3
F
F
(along z axis) bonds. This
CuII
MnIII
is known as Z-out case. The
H3N
NH3
F
F
1.79
2.07
Jahn-Teller effect is more
pronounced
when
the
former eg level is not
F
NH3
completely filled (d1 > d2),
9
4
d
d
that is for configurations d4 (high spin), d7 (low spin) and d9. In these cases a static JahnTeller effect can be observed and the species of D4h symmetry can exist in a solid phase.
We can now clearly see that Ti3+ with one d electron would prefer z-in as here the
electronic degeneracy is removed and the energy is lowered (2/3 δ2). In contrast V3+ with
a d2 configuration would prefer a z-out configuration. The Cr3+ has a d3 configuration and
in an octahedral crystal field it is not electronically degenerate. Therefore the question of
distortion does not arise. Two further points need to be emphasized. One, the energy
separations caused as a result of the distortion are much smaller in comparison to the
original separation between t2g and eg levels and also naturally in comparison with pairing
energies. Two, the distortions are better manifested when the electronically degenerate
state occurs in the eg levels rather than in the t2g levels (because the effect of distortion is
more directly felt). However, it is not possible to predict the type of distortion when the
electronic degeneracy occurs in the eg levels. Consequently a number of Cu2+ complexes
in an octahedral environment show Jahn-Teller distortion. Although theoretically one is
unable to predict the type of distortion that would occur in these molecules,
experimentally it is found that elongation (z-out) is preferred.
∆ο >> δ1 > δ2.