Download MAT 360 Lecture 6 - Stony Brook Mathematics

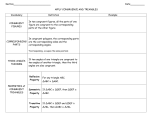
MAT 360 Lecture 6
Hilbert Axioms
Congruence
To come
MLC
 Sketchpad projects
 Midterm – 4 problems





Models and interpretation.
Proof from Hilbert’s axioms
Produce a definition of some known object
Definitions of terms we learn (like
independence, categorical) will not be asked
directly but “applied”
Congruence Axiom 1

If A and B are distinct points then for any
point A’ and for each ray r emanating
from A’ there exist a unique point B’ on r
such that B’≠ A’ and AB ~ A’B’.
Recall we have an undefined term

CONGRUENT

This term will be used in two ways:
1. Segment CD is congruent to segment EF
2. Angle <A is congruent to angle <B

Question: Could we use different words
for the use 1. and the use 2?
Congruence Axiom 2
If AB ~ CD and AB ~ EF then CD ~ EF
 AB ~ AB

Prove that
segment AB is congruent to segment BA
 If AB ~ CD then CD ~ AB

Congruence Axiom 3

If





A*B*C,
A’*B’*C’,
AB ~ A’B’
BC ~ B’C’
Then AC ~ A’C’
Congruence Axiom 4
Given an angle <BAC, a ray A’B’ and a
side of the line A’B’ there is a unique ray
A’C’ emanating from the point A’ such
that

<BAC < B’A’C’

Congruence Axiom 5
If <A ~ <B and <A ~ <C then <B ~ <C.
 <A~<A

Proposition

If <A ~ <B then <B ~ <A
Definition

Two triangles are congruent if there is
a one to one correspondence between the
vertices so that the corresponding sides
are congruent and the corresponding
angles are congruent.

NOTE: This is third use of the word
“congruent.”.
Congruence Axiom 6 (SAS)

If two sides and the included angle of a
triangle are congruent respectively to two
sides and the included angle of another
triangle then the two triangles are
congruent.
Proposition

Given a triangle ΔABC and a segment DE
such that DE~AB there is a unique point F
on a given side of the line DE such that
the ΔABC~ΔDEF
Proposition

If in ΔABC we have that AB~AC then
<B~<C.
Definition

The symbols AB<CD mean that there
exists a point E between C and D such
that AB~CE.

The symbols CD>AB have the same
meaning.

Proposition

Exactly one of the following conditions
holds

AC<CD, AB~C or AB>CD
If AB<CD and CD~EF then AB<EF.
 If AB>CD and CD~EF then AB>EF.
 If AB<CD and CD<EF then AB<EF.

More Propositions
Supplements of congruent angles are
congruent.
 Vertical angles are congruent to each
other
 An angle congruent to a right angle is a
right angle.
 For every line l and every point P there
exists a line through P perpendicular to l.

Definition
Suppose that there exists a ray EG
between ED and EF such that

<ABC ~ <GEF.
 Then we write <ABC < <DEF.

Proposition

Exactly one of the following holds

<P < <Q , <Q < <P or P ~ Q.
If <P<<Q and <Q~<R then<P <<R
 If <P ><Q and <Q~<R then<P > <R
 If <P <<Q and <Q<R then <P<<R

(typo)
Proposition (SSS)
Given triangles ΔABC and ΔDEF. If
AB~DE, BC~EF and AC~DF then

ΔABC~ ΔDEF


Note: from now on, in the slides, we
denote congruence by ~
Proposition

All right angles are congruent with each
other.