Download Linearization and Newton*s Method

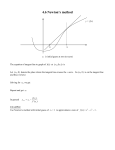
LINEARIZATION AND
NEWTON’S METHOD
Section 4.5
Linearization
• Algebraically, the principle of local linearity means that the
equation of the tangent line defines a function that can be
used to approximate a differentiable function near the
point of tangency,
• The equation of the tangent line is given a new name: the
linearization of f at a.
• Recall point-slope form of a line: y=m(x-x1)+y1
• The tangent line at (a, f(a)) can be written:
y=f ’(a)(x-a)+f(a)
Linearization
So the equation of the tangent line at a = 1 is
(These are y-values…. Find the x that goes with it!
Tangent Line Equation:
Newton’s Method
1 2
f  x  x  3
2
Finding a root for:
5
4
3
We will use Newton’s
Method to find the root
between 2 and 3.
2
1
-4
-3
-2
-1
0
1
2
3
4
-1
-2
-3

1 2
f  x  x  3
2
1.5
f  x  x
1.5
2
z 3
3
1 2
f  3   3  3  1.5
2
Guess:
mtangent  f   3  3
(not drawn to scale)
1.5
3
z
1.5
3
 2.5
(new guess)
3
1.5
z
3

1 2
f  x  x  3
2
1.5
f  x  x
2.5
1
2
f  2.5    2.5   3  .125
2
Guess:
2
z
3
mtangent  f   2.5  2.5
.125
2.5 
 2.45
2.5 (new guess)
.125
z
2.5

1 2
f  x  x  3
2
1.5
f  x  x
Guess:
2.45
f  2.45  .00125
z
2
3
mtangent  f   2.45  2.45
.00125
2.45 
 2.44948979592
2.45
.00125
z
2.45
(new guess)

Guess:
2.44948979592
f  2.44948979592  .00000013016
Amazingly close to zero!
This is Newton’s Method of finding roots. It is an example of an algorithm (a
specific set of computational steps.)
It is sometimes called the Newton-Raphson method
This is a recursive algorithm because a set of steps are repeated with the
previous answer put in the next repetition. Each repetition is called an
iteration.

Guess:
2.44948979592
f  xn 
f  2.44948979592

.00000013016
Newton’s Method: 
xn 1  xn 
f   xn 
Amazingly close to zero!
This is Newton’s Method of finding roots. It is an example of an algorithm (a
specific set of computational steps.)
It is sometimes called the Newton-Raphson method
This is a recursive algorithm because a set of steps are repeated with the
previous answer put in the next repetition. Each repetition is called an
iteration.

y  x3  x crosses y  1 .
1  x 3  x 0  x 3  x  1 f  x   x3  x  1
Find where
n
0
1
xn
1
1.5
f  xn 
1
.875
f  xn 
xn 1  xn 
f   xn 
f   xn 
2
1
1
 1.5
2
5.75
.875
1.5 
 1.3478261
5.75
2 1.3478261 .1006822 4.4499055
1.3252004 
3
f   x   3x 2  1
1.3252004
 1.3252004  1.0020584
1

There are some limitations to Newton’s method:
Looking for this root.
Bad guess.
Wrong root found
Failure to converge
