Download Numerical Analysis of Quantum Graphs

Numerical Analysis of Quantum Graphs
Michele Benzi
Department of Mathematics and Computer Science
Emory University
Atlanta, Georgia, USA
Householder Symposium XIX
Spa, Belgium
8-13 June, 2014
1
Outline
1
Motivation
2
Basic definitions
3
Boundary conditions at the vertices
4
Discretization
5
Numerical experiments
6
Time-dependent problems
7
Conclusions and open problems
2
Acknowledgements
Joint work with Mario Arioli (Berlin)
Support: NSF, Emerson Center for Scientific Computation, Berlin
Mathematical School, TU Berlin
3
Outline
1
Motivation
2
Basic definitions
3
Boundary conditions at the vertices
4
Discretization
5
Numerical experiments
6
Time-dependent problems
7
Conclusions and open problems
4
Motivation
The purpose of this talk is to introduce the audience to a class of
mathematical models known as quantum graphs, and to describe some
numerical methods for investigating such models.
Roughly speaking, a quantum graph is a collection of intervals glued
together at the end-points (thus forming a metric graph) and a differential
operator (“Hamiltonian") acting on functions defined on these intervals,
coupled with suitable boundary conditions at the vertices.
5
Motivation (cont.)
Quantum graphs are becoming increasingly poular as mathematical models
for a variety of physical systems including conjugated molecules (such as
graphene), quantum wires, photonic crystals, carbon nanostructures, thin
waveguides, etc.
G. Berkolaiko and P. Kuchment, Introduction to Quantum Graphs, American
Mathematical Society, Providence, RI, 2013.
6
Example: Graphene
7
Example: Carbon nanostructures
8
Example: Polystyrene
9
Motivation (cont.)
Other potential applications include the modeling of phenomena such as
information flow, diffusion and wave propagation in complex networks
(including social and financial networks), blood flow in the vascular
network, electrical signal propagation in the nervous system, traffic flow
simulation, and so forth.
10
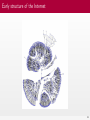
Early structure of the Internet
11
Motivation (cont.)
While the theory of quantum graphs is very rich (well-posedness results,
spectral theory, etc.), there is very little in the literature on the numerical
analysis of such models.
In this lecture we consider numerical methods for the analysis of quantum
graphs, focusing on simple model problems.
This is still very much work in progress!
12
Outline
1
Motivation
2
Basic definitions
3
Boundary conditions at the vertices
4
Discretization
5
Numerical experiments
6
Time-dependent problems
7
Conclusions and open problems
13
Combinatorial graphs
A combinatorial graph Γ is a pair (V, E) where V = {vj }N
j=1 is a set of
vertices, or nodes, and E = {ek }M
k=1 is a set of edges connecting the
vertices.
Each edge e can be identified by the couple of vertices that it connects
(e = (vi , vj )).
The edges simply stand for some type of binary relation between pairs of
nodes: in particular, they are not endowed with any geometry.
Only undirected graphs are considered here. In some cases it will be
necessary to assign a direction to the edges, but the choice will be
arbitrary.
14
Some matrices associated with combinatorial graphs
Adjacency matrix A: symmetric N × N vertex-to-vertex Boolean
structure, Aij = 1 iff edge (vi , vj ) exists.
Incidence matrix E: rectangular N × M vertex-to-edge matrix. Each
column corresponds to an edge e = (vi , vj ) and has only two non zero
entries, 1 and −1, in position i and j (the sign is arbitrary and will be
immaterial for our purposes).
Combinatorial Laplacian: LΓ = EET = DΓ − A, where DΓ is the
diagonal matrix of degrees.
I
I
E can be interpreted as a discrete divergence and ET as a discrete
gradient.
If Γ is connected, Ker(ET ) is the 1D subspace of RN spanned by
e = (1, 1, . . . , 1)T .
LΓ is a positive semidefinite singular matrix with Ker(LΓ ) = span{e}
15
Example: graphene sheet
5
4
3
2
1
0
1
2
3
4
5
6
7
8
16
Example: graphene sheet (cont.)
17
Example: graphene sheet (cont.)
18
Beyond simple graphs
While combinatorial graphs (including weighted and directed ones) have
long been found extremely useful in countless applications, they are too
simple for modeling certain types of phenomena on networks.
In many cases, the interaction between pairs of nodes may be more
complex than just a 0-1 relation.
19
Beyond simple graphs (cont.)
For instance, in physics and engineering applications the edges may
represent actual physical links between vertices, and these links will
typically be endowed with a notion of length.
Hence, communication between nodes may require some time rather
than being instantaneous.
This simple observation is formalized in the notion of metric graph.
20
Metric graphs
A graph Γ is a metric graph if to each edge e is assigned a measure
(normally the Lebesgue one) and, consequently, a length le ∈ (0, ∞).
Thus, each edge can be assimilated to a finite interval on the real line
(0, le ) ⊂ R, with the natural coordinate s = se .
Note that we need to assign a direction to an edge in order to assign a
coordinate to each point on e. For this we can take the (arbitrarily chosen)
direction used in the definition of the incidence matrix of Γ.
In technical terms, a metric graph is a topological manifold (1D simplicial
complex) having singularities at the vertices, i.e. it is not a differentiable
manifold (globally).
21
Metric graphs (cont.)
The points of a metric graph Γ are the vertices, plus all the points on the
edges.
The Lebesgue measure is well-defined on all of Γ for finite graphs (the only
ones considered here). Thus, Γ is endowed with a global metric.
The distance between two points (not necessarily vertices) in Γ is the
length of the geodetic (shortest path) between them.
Note that Γ is not necessarily embedded in a Euclidean space Rn .
22
Metric graphs (cont.)
The edges may also have physical properties, such as conductivity,
diffusivity, permeability etc., that are are not well represented by a single
scalar quantity, as in a weighted graph. Some of these quantities could
even change with time.
In other words, interactions between nodes may be governed by laws,
which could be described in terms of differential equations.
One can easily imagine similar situations also for other types of networks,
including social or financial networks.
Formalization of this notion leads to the concept of quantum graph.
23
Hilbert spaces on Γ
To define a quantum graph, we need first to introduce certain Hilbert
spaces of functions defined on a metric graph Γ.
R
Let L2 (e) := f : e → R | e |f |2 ds < ∞ .
Definition: The space of square-integrable functions on Γ is defined as
M
L2 (Γ) :=
L2 (e) .
e∈E
In other terms,
f ∈ L2 (Γ)
iff
kf k2L2 (Γ) =
X
kf k2L2 (e) < ∞.
e∈E
24
Hilbert spaces on Γ (cont.)
Next, consider the Sobolev space
Z
H 1 (e) = f ∈ L2 (e) | |f 0 (s)|2 ds < ∞ .
e
Definition: The Sobolev space H 1 on Γ is defined as
!
M
1
1
H (Γ) =
H (e) ∩ C 0 (Γ)
e∈E
where C 0 (Γ) is the space of continuous functions on Γ.
In other terms,
f ∈ H 1 (Γ) iff
f is continuous and kf k2H 1 (Γ) =
X
kf k2H 1 (e) < ∞ .
e∈E
25
Quantum graphs (def.)
Let H be a linear differential operator defined on suitable subspace
D(H) ⊂ L2 (Γ). We will call H a Hamiltonian on Γ.
Definition: A quantum graph is a metric graph Γ together with a
Hamiltonian H and boundary (vertex) conditions that ensure that H
is self-adjoint.
Hence, a quantum graph is a triple (Γ, H, vertex conditions).
In some situations the definition may be altered to allow more general
(non-self-adjoint, pseudo-) differential operators.
Remark: Although the concept goes back at least to G. Lumer (1980),
the name “quantum graph" was introduced by T. Kottos and U. Smilansky
(Phys. Rev. Lett. 79 (1997), pp. 4794–4797) and has since become
universally adopted.
26
Hamiltonians
We will focus primarily on the simplest example of a Hamiltonian: the
(negative) second derivative operator
d2 u
.
ds2
We will also consider Schrödinger operators
u → Hu = −
d2 u
+ V (s)u ,
ds2
where V is a potential, usually required to be bounded from below. Here
we assume u ∈ H 2 (e), ∀e ∈ E.
u → Hu = −
More complicated operators can also be considered, for example the magnetic
Schrödinger operator
2
1 d
u → Hu =
− A(s) u + V (s)u
i ds
as well as higher order operators, Dirac operators, pseudo-differential operators,
etc.
27
Outline
1
Motivation
2
Basic definitions
3
Boundary conditions at the vertices
4
Discretization
5
Numerical experiments
6
Time-dependent problems
7
Conclusions and open problems
28
Examples of boundary conditions
In this talk we only consider the so-called Neumann-Kirchhoff conditions, a
special case of δ-type conditions:

 f (s) is continuous on Γ
P
df
(v) = αv f (v)
 ∀v ∈ Γ
e∈Ev
dse
Ev is the subset of the edges having v as a boundary point.
The αv ’s are fixed real numbers.
29
Examples of boundary conditions (cont.)
The Hamiltonian is associated to the following quadratic form on H 1 (Γ):
XZ X
f 0 (s)2 ds +
h[f, f ] =
αv |f (v)|2 .
e∈E
e
v∈V
The case αv ≡ 0 corresponds to the Neumann-Kirchhoff conditions:

 f (s) is continuous on Γ
P
df
(v) = 0
 ∀v ∈ Γ
e∈Ev
dse
and the corresponding quadratic form reduces to
XZ f 0 (s)2 ds.
h[f, f ] =
e∈E
e
30
Examples of boundary conditions (cont.)
The Neumann-Kirchhoff conditions are also called the standard vertex
conditions. They are the natural boundary conditions satisfied by the
Schrödinger operator.
The first condition expresses continuity, while the second can be
interpreted as conservation of current.
31
Examples of boundary conditions (cont.)
We observe that, on the other hand, the Dirichlet or Neumann boundary
conditions at the vertices are examples of decoupling conditions and are of
little interest in this context, except for vertices of degree one.
For example, if we impose the vertex Dirichlet condition f (v) = 0 at each
vertex, the Hamiltonian is just the direct sum of the operators on each
edge e with Dirichlet conditions on the end; hence, the quantum graph
decouples into a set of independent intervals, and the topology of the
graph becomes irrelevant.
32
Outline
1
Motivation
2
Basic definitions
3
Boundary conditions at the vertices
4
Discretization
5
Numerical experiments
6
Time-dependent problems
7
Conclusions and open problems
33
Finite element discretization
Self-adjoint elliptic equations can be formulated as variational problems for
an energy functional.
Given a function g ∈ L2 (Γ), the minimum problem is
min J(u) ,
u∈H 1 (Γ)
where
1X
J(u) =
2
e∈E
Z
e
0
2
2
u (s) + V (s)u(s)
ds −
XZ
e∈E
g(s)u(s) ds.
e
We discretize the problem using 1D linear finite elements on each edge
and use a domain decomposition approach:
first we eliminate the unknowns associated with points inside the edges,
then we use the Neumann-Kirchhoff conditions and the values of the
derivative at the vertices to form and solve a reduced-size linear system
(Schur complement) for the values of the solution at the vertices.
34
Finite element discretization (cont.)
On each edge of the quantum graph it is possible to use the classical 1D
finite-element method. Let e be a generic edge identified by two vertices,
which we denote by va and vb .
The coordinate s will parameterize the edge such that for s = 0 we have
the vertex va and for s = `e we have the vertex vb .
The first step is to subdivide the edge in ne intervals of length he . The
points
e n−1
sj j=1 ∪ {va } ∪ {vb }
form a chain linking va to vb lying on e.
35
Finite element discretization (cont.)
Denoting by













n on+1
ψje
the standard hat basis functions, we have
j=0
ψ0e (s)
ψje (s)
1−
0
s
h
(
1−
0
|sj −s|
h
=
=










1−
e

 ψne +1 (s) =
0
if 0 ≤ s ≤ he
otherwise
`e −s
h
if sj−1 ≤ s ≤ sj+1
otherwise
.
(1)
if `e − he ≤ s ≤ `e
otherwise
The functions ψje are a basis for the finite-dimensional space
n
o
Vhe = uh ∈ H 1 (e) : uh |[sej ,sej+1 ] ∈ P1 , j = 0, . . . , n + 1 ,
where P1 is the space of linear functions.
36
Finite element discretization (cont.)
In practice, we subdivide each edge, forming a chain made of nodes of
degree 2, and we build the usual hat functions extending them to the
vertices:
37
Finite element discretization (cont.)
Globally, we construct the finite element space
M
Vh (Γ) =
Vhe ,
e∈E
which is a finite-dimensional subspace of H 1 (Γ).
The continuity on Γ of the functions in Vh follows by construction: at each
vertex v we have dv (degree of the vertex v) linear functions that take the
value 1 on v, each one belonging to an independent Vhe with e ∈ Ev .
Any function uh ∈ Vh (Γ) is then a linear combination of the ψje :
uh (s) =
X n+1
X
αje ψje (s).
e∈E j=0
38
Finite element discretization (cont.)
The quadratic form h of the Hamiltonian operator can be tested on all the
ψ’s and we have the following finite dimensional (discrete) bilinear form:
hh [uh , ψke ]
=
X
X n+1
e∈E j=0
αje
Z
e
dψje dψke
ds +
ds ds
Z
V
(s)ψje ψke
ds .
e
In both h and hh the Neumann-Kirchhoff conditions at each vertex are the
natural conditions and they are automatically satisfied.
39
Extended graph
The nodes on the edges will describe a chain path between two vertices.
We can then think of introducing a new (combinatorial) graph in which
the nodal discretization points become additional vertices and the edges
are obtained by subdividing the edges of the original (metric) graph. We
call this the extended graph associated with Γ and denote it by G.
Assuming for simplicity that all edges e ∈ E have equal length and that
the same number n − 1 of internal nodes are used for each edge, the new
graph G will have (n − 1) × M + N vertices and n × M edges, where N is
the number of vertices and M the number of edges in Γ.
The extended graph can be huge, but it has a lot of structure.
40
Extended graph (cont.)
It is natural to order the vertices according to the original order of the
edges so that the new (“subdomain") vertices on the edges are numbered
contiguously, and the vertices of the original graph (“separators") are
numbered last.
The resulting Gramian matrix H = (hh [ψje , ψke ]) is of the form
H=
H11 H12
HT12 H22
where H11 is a block diagonal symmetric and positive definite matrix
where each diagonal block is of size n − 1 and tridiagonal, and H22 is a
diagonal matrix with positive diagonal entries.
Important: We are assuming that the potential V (s) is positive.
41
A simple example
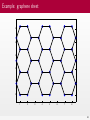
Figure: Example of a simple planar metric graph and of its incidence matrix.
42
A simple example
Figure: Example of the extension of the graph when a 4 nodes chain is added
internally to each edge (left) and its incidence matrix (right).
42
A simple example
Figure: Pattern of the discrete Hamiltonian H where the red bullets correspond
to the original vertices and the blue ones to the internal nodes on each edge.
42
Extended graph (cont.)
2
d
In the special case V = 0 (that is, H = − ds
2 , we obtain the discrete
(negative) Laplacian (stiffness matrix) L on G.
When the same number of (equidistant) discretization points is used on
each edge of Γ, L coincides (up to the factor h−1 ) with the combinatorial
graph Laplacian LG .
Both the stiffness matrix L and the mass matrix M = (hψje , ψke i) have a
block structure matching that of H. For example, if V (s) = k (constant)
then H = L + kM.
Minimization of the discrete quadratic form
Jh (uh ) := hh [uh , uh ] − 2hgh , uh i,
uh ∈ Vh (Γ)
is equivalent to solving the extended linear system Huh = gh , of order
(n − 1)M + N .
43
Solution of the extended linear system
The extended linear system can be solved efficiently by block LU
factorization, by first eliminating the interior edge nodes (this requires
solving, in parallel if one wishes, a set of M independent tridiagonal
systems of order n − 1), and then solving the N × N Schur complement
system
e
Suvh = ghv − HT12 H−1
11 fh ≡ ch
for the unknowns associated with the vertices of Γ.
44
Solution of the extended linear system
The block LU factorization of H is given by
H11 H12
H11 O
I H−1
H12
11
H=
=
.
HT12 H22
HT12 S
O
I
Simple, yet crucial observation: the Schur complement
S = H22 − HT12 H−1
11 H12
is a sparse matrix.
45
Back to the simple example
Figure: The pattern of the Schur complement S.
46
Solution of the extended linear system (cont.)
Theorem: The nonzero pattern of the Schur complement
S = H22 − HT12 H−1
11 H12
coincides with that of LΓ , the (combinatorial) graph Laplacian of the
(combinatorial) graph Γ.
In the special case V = 0, we actually have S = LΓ .
47
Solution of the extended linear system (cont.)
Note that S is SPD, unless V = 0 (in which case S is only positive
semidefinite).
For Γ not too large, we can solve the Schur complement system by sparse
Cholesky factorization with an appropriate reordering.
However, for large and complex graphs (for example, scale-free graphs),
Cholesky tends to generate enormous amounts of fill-in, regardeless of the
ordering used.
Hence, we need to solve the Schur complement system by iterative
methods, like the preconditioned conjugate gradient (PCG) algorithm.
48
Solution of the extended linear system (cont.)
Preconditioning of matrices arising from complex graphs is an active area
of research.
Some of the techniques that work well for other types of problems (like
Incomple Cholesky Factorization) are useless here.
Here we consider two simple preconditioners:
diagonal scaling with D = diag(S)
a first degree polynomial preconditioner:
P−1 = D−1 + D−1 (D − S)D−1 ≈ S−1 .
Note: For the very sparse matrices considered here, each iteration of PCG with
polynomial preconditioning costs about the same as 1.5 iterations with diagonal
preconditoning.
49
Outline
1
Motivation
2
Basic definitions
3
Boundary conditions at the vertices
4
Discretization
5
Numerical experiments
6
Time-dependent problems
7
Conclusions and open problems
50
Numerical experiments
We present first results for a simple steady-state (equilibrium) problem
−
d2 u
+V u=g
ds2
on Γ
with Neumann-Kirchhoff conditions at the vertices, for three different
choices of Γ:
yeast, the PPI network of beer yeast (N = 2224, M = 6609)
drugs, a social network of drug addicts (N = 616, M = 2012)
pref2000, a synthetic scale-free graph constructed using the
preferential attachment scheme (N = 2000, M = 3974)
In each case we assume that all edges have unit length and we use n = 20
1
interior discretization points per edge (h = 21
).
For the potential we use V (s) = k(s − 12 )2 and V (s) = k (const.) for
k = 0.1, 1, 10.
51
PPI network of Saccharomyces cerevisiae (beer yeast)
52
Social network of injecting drug users in Colorado Springs
Figure courtesy of Ernesto Estrada.
53
Scale-free Barabási–Albert graph (pref)
54
Numerical experiments (cont.)
The sizes of the extended system Huh = gh and of the reduced system
Suvh = ch are, respectively:
n = 134, 404, N = 2224 for yeast;
n = 40, 856, N = 616 for drugs;
n = 81, 480 and N = 2000 for pref2000.
The Schur complement can be formed efficiently since it is very sparse and
we know the location of the nonzero entries in advance.
Since the original graphs are very small, the Schur complement system is
best solved by sparse Cholesky factorization, but we also experiment with
PCG. Without preconditioning, convergence can be slow.
For each problem we also need to solve M uncoupled tridiagonal systems
of order 20.
55
Numerical experiments (cont.)
Problem
yeast
drugs
pref2000
V (s) = k(s − 12 )2
k = 0.1
k=1
It rel. error It rel. error
13 3.3e-08 10 1.6e-08
10 1.4e-08
8
1.9e-08
9
2.9e-09
8
3.3e-10
Results of running pcg (T OL =
diagonal preconditioner.
√
It
8
6
6
k = 10
rel. error
4.8e-10
4.4e-09
1.4e-09
eps) on Schur complement system,
The “exact" solution is the one returned by backslash.
56
Numerical experiments (cont.)
Problem
yeast
drugs
pref2000
It
7
6
5
V (s) = k(s − 12 )2
k = 0.1
k=1
k = 10
rel. error It rel. error It rel. error
5.9e-08 6 1.5e-09 5 1.3e-11
3.9e-08 5 1.7e-09 4 1.2e-10
4.5e-09 5 2.4e-11 4 3.1e-11
Results of running pcg (T OL =
polynomial preconditioner.
√
eps) on Schur complement system,
57
Numerical experiments (cont.)
Problem
yeast
drugs
pref2000
k = 0.1
It rel. error
36 7.7e-09
42 6.9e-09
23 3.5e-09
Results of running pcg (T OL =
diagonal preconditioner.
√
V (s) = k
k=1
It rel. error
14 1.4e-08
14 9.0e-09
12 1.1e-08
It
5
5
5
k = 10
rel. error
6.2e-09
4.9e-09
2.5e-09
eps) on Schur complement system,
58
Numerical experiments (cont.)
Problem
yeast
drugs
pref2000
k = 0.1
It rel. error
20 4.0e-09
24 4.6e-08
13 9.2e-10
Results of running pcg (T OL =
polynomial preconditioner.
√
V (s) = k
k=1
It rel. error
8 2.1e-08
9 2.3e-09
8 1.2e-09
It
4
4
4
k = 10
rel. error
5.6e-10
4.3e-10
2.2e-10
eps) on Schur complement system,
59
Numerical experiments (cont.)
Matrix S−1 for pref graph, k = 0.1.
60
Numerical experiments (cont.)
Matrix S−1 for pref graph, k = 1.
61
Numerical experiments (cont.)
Matrix S−1 for pref graph, k = 10.
62
Numerical experiments (cont.)
N
2000
5000
10000
No prec.
83
108
125
Diagonal
23
23
23
Polynomial
13
13
13
PCG iteration counts for pref graph, V (s) = k = 0.1, increasing N .
Note: Here h is constant, the size N of the graph Γ is increasing.
The size of the extended graph G is n = 81, 480, n = 204, 360, and
n = 409, 300, respectively.
63
Numerical experiments (cont.)
h−1
21
41
81
101
No prec.
83
83
82
83
Diagonal
23
23
22
21
Polynomial
13
13
12
12
PCG iteration counts for pref graph, V (s) = k = 0.1, N = 2000.
Note: Here h is decreasing, the size N of Γ is fixed. The size of the
extended graph G increases from 81,480 to 399,400 vertices.
With diagonal or polynomial preconditioning the solution algorithm is
scalable with respect to both N and h for these graphs.
64
Outline
1
Motivation
2
Basic definitions
3
Boundary conditions at the vertices
4
Discretization
5
Numerical experiments
6
Time-dependent problems
7
Conclusions and open problems
65
The parabolic case
Among our goals is the analysis of diffusion phenomena on metric graphs.
In this case, we assume that the functions we use also depend on a second
variable t representing time, i.e.,
u(t, s) : [0, T ] × Γ −→ R.
A typical problem would be:
given u0 ∈ H 1 (Γ)and a f ∈ L2 [0, T ], L2 (Γ)
find u ∈ L2 [0, T ], H 1 (Γ) ∩ C 0 [0, T ]; H 1 (Γ) such that

∂u ∂ 2 u



− 2 + mu = f
on Γ
∂t
∂s



u(0, s) = u0 ,
where m ≥ 0.
Similarly, we can define the wave equation and the Schrödinger equation
on Γ.
66
The parabolic case (cont.)
Space discretization using finite elements leads to the semi-discrete system
Mu̇h = Huh + fh ,
uh (0) = uh,0 ,
where uh = uh (t) is a vector function on the extended graph G, and the
mass matrix M and Hamiltonian H are as before.
A variety of methods are available for solving this linear system of ODEs:
backward Euler, Crank-Nicolson, exponential integrators based on Krylov
subspace methods, etc.
Note that for large graphs and/or small h, this can be a huge system.
We have obtained some preliminary results using Stefan Güttel’s code
funm_kryl for evaluating the action of the matrix exponential on a vector.
67
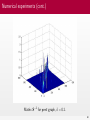
Solution of diffusion problem on Γ for different times.
68
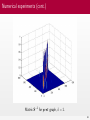
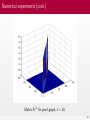
Solution of diffusion problem on Γ for different times.
68
Outline
1
Motivation
2
Basic definitions
3
Boundary conditions at the vertices
4
Discretization
5
Numerical experiments
6
Time-dependent problems
7
Conclusions and open problems
69
Summary
Quantum graphs bring together disparate areas: physics, graph
theory, PDEs, spectral theory, complex networks, finite elements,
numerical linear algebra...
On the surface just a huge set of “trivial" 1D problems, but the
complexity of the underlying graph and the Neumann-Kirchhoff
coupling conditions make life interesting!
Linear systems are huge but highly structured with much potential for
order reduction and parallelism.
Challenges ahead include:
I
I
I
I
I
I
Analyze PCG convergence
Eigenvalue problems
Hyperbolic problems (shocks)
Schrödinger, Dirac equations (important for graphene)
Non-self-adjoint and non-linear problems, non-local operators, etc.
Applications to real world problems
There is a lot of work to do in this area!
70