Download January 11

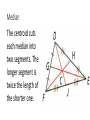
Geometry
January 11, 2017
Chapter 5 REVIEW
DO NOW
Agenda
• Announcements (2nd hour only)
• Do Now
• Review
• Practice
I can identify and apply
triangle midsegments,
medians, and altitudes.
Review: Midpoint
The midpoint is the point
exactly halfway between two
other points.
Midsegment Properties
A midsegment
is exactly half
the length of its
parallel side.
Practice (Midsegments shown)
(1) Determine all
missing segment
lengths.
Practice (Midsegments shown)
(2) List all pairs of
parallel segments.
Perpendicular Bisector
If 𝐶𝐷 is the
perpendicular
bisector of 𝐴𝐵,
then 𝐴𝐶 ≅ 𝐵𝐶.
PRACTICE: Calculate x
Angle Bisector
Every point on an
angle bisector is
equidistant to the
two sides of the
angle.
PRACTICE: Calculate x
Point of Concurrency
The three perpendicular
bisectors of a triangle
will intersect at a single
point. This is called the
point of concurrency.
Point of Concurrency
This point of
concurrency is
equidistant from all
vertices (corners) of
the triangle.
Circumcenter
This point is called the
circumcenter.
It is the center of the
smallest circle the
triangle will fit inside.
Circumcenter
The circumcenter can be inside, on,
or outside a triangle.
Finding the circumcenter
You only need to draw TWO of the perpendicular bisectors.
Median
Point of
concurrency:
Centroid
(Center of
gravity)
Median
The centroid cuts
each median into
two segments. The
longer segment is
twice the length of
the shorter one.
Practice
Hint: median segment lengths are in
the ratio 1 : 2 : 3
Altitude
The altitude of a
triangle is
perpendicular to
one side and goes
through the
opposite vertex.
Altitude
Altitudes can intersect inside, on, or outside
the triangle.
Triangle Inequalities
Larger angles are always opposite larger sides
(and vice versa).
Triangle Inequalities
The lengths of the two shorter sides of a
triangle are more than the length of the
longest side.
Hinge Theorem (aka SAS/SSS Inequality)
∠𝐴 > ∠𝑋 ⇔ 𝐵𝐶 > 𝑌𝑍
Hinge Theorem (aka SSS Inequality)
• What are the possible values of x:
• What is the lowest it could be?
• What is the highest it could be?