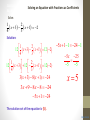Download 2.3 More on Solving Linear Equations

2.3 More on Solving
Linear Equations
Objective 1
Learn and use the four steps for solving
a linear equation.
Slide 2.3-3
Learn and use the four steps for solving a linear equation.
We solve more complicated equations using the following four-step method.
Solving a Linear Equation
Step 1: Simplify each side separately. Clear parentheses, fractions, and
decimals, using the distributive property as needed, and combine all
like terms.
Step 2: Isolate the variable term on one side. Use the addition
property if necessary so that the variable term is
on one side
of the equation and a number is on the other.
Step 3: Isolate the variable. Use the multiplication property if
necessary to get the equation in the form x = a number.
(Other letters may be used for variables.)
Step 4: Check. Substitute the proposed solution into the original
equation to see if a true statement results.
Slide 2.3-4
CLASSROOM
EXAMPLE 1
Applying Both Properties of Equality to Solve an Equation
Solve.
5 p  4  19
Solution:
Check:
5 p  4  4  19  4
5(3)  4  19
5 p  15
15  4  19
5 p 15

5 5
19  19
p  3
The solution set of the equation is {−3}.
Slide 2.3-5
CLASSROOM
EXAMPLE 2
Applying Both Properties of Equality to Solve an Equation
Solve.
5  8x  2 x  5
Solution:
Check:
5  8x  2 x  2 x  5  2 x
5 10x  5
5 10x  5  5  5
10 x 10

10 10
x 1
5  8(1)  2(1)  5
3  3
The solution set of the equation is {1}.
Remember that the variable can be isolated on either side of the equation. There
are often several equally correct ways to solve an equation.
Slide 2.3-6
CLASSROOM
EXAMPLE 3
Using Four Steps to Solve an Equation
Solve.
11  3  x  1  5x  16
Solution:
Check:
11  3x  3  5x 16
11  3  x  1  5x  16


14  3x  5x  5x 16  5x 11  3  1  1  5  1  16
14  2x 14  16 14
11  3 0  5  16
2 x 2
11  11

2 2
x  1
The solution set of the equation is {−1}.
Slide 2.3-7
CLASSROOM
EXAMPLE 4
Using the Four Steps to Solve an Equation
Solve.
4 x  ( x  7)  9
Solution:
Check:
4 x  1( x  7)  9
4x  x  7  9
3x  7  7  9  7
3 x 16

3
3
16
x
3
The solution set of the equation is
4 x  ( x  7)  9
 16    16  
4      7  9
 3   3  
64  16 21  27
   
3  3 3 3
64  37  27
  
3  3  3
27 27

3
3
16 
 .
3
Slide 2.3-8
Learn and use the four steps for solving a linear equation.
(cont’d)
Be very careful with signs when solving an equation like the one in the
previous example. When clearing parentheses in the expression
remember that the − sign acts like a factor of −1 and affects the sign of
every term within the parentheses.
Slide 2.3-9
CLASSROOM
EXAMPLE 5
Using the Four Steps to Solve an Equation
Solve.
2  3  2  6 z   4  z  1  8
Solution:
Check:
2  6 18z  4z  4  8
4 18z  4z  4z  4  4z
4  22 z  4  4  4
22 z
0

22 22
z 0
2  3  2  6 z   4  z  1  8
2  3 2  6  0  4  0  1  8
2  3(2  0)  4  0  8
2  6  0  0 8
2  12  14
14  14
The solution set of the equation is {0}.
Slide 2.3-10
Objective 2
Solve equations with fractions or
decimals as coefficients.
Slide 2.3-11
Solve equations with fractions or decimals as coefficients.
We clear an equation of fractions by multiplying each side by the least
common denominator (LCD) of all the fractions in the equation. It is a
good idea to do this to avoid messy computations.
When clearing an equation of fractions, be sure to multiply every term on each
side of the equation by the LCD.
Slide 2.3-12
CLASSROOM
EXAMPLE 6
Solving an Equation with Fractions as Coefficients
Solve.
1
5
3 1
x
  x
3
12 4 2
Solution:
Check:
1
5
3
1
12  x  12   12   12  x
3
12
4
2
4x  5  4x  9  6x  4x
5  9  9  2x  9
14 2 x

2
2
x  7
The solution set of the equation is {−7}.
1
5
3 1
x
  x
3
12 4 2
1
5
3 1
 7      7 
3
12 4 2
7 5
3 7

 
3 12 4
2
28 5
9
42



12 12 12
12
33 33

12
12
Slide 2.3-13
CLASSROOM
EXAMPLE 7
Solving an Equation with Fractions as Coefficients
Solve.
1
2
x

3


  x  1  2
4
3
Solution:
2
1

12   x  3   x  1   12  2 
3
4

1

 2

12   x  3   12    x  1   12(2)
4

 3

3( x  3)  8( x  1)  24
3x  9  8x  8  24
5x 1 1  24 1
5 x 25

5
5
x 5
5x 1  24
The solution set of the equation is {5}.
Slide 2.3-14
CLASSROOM
EXAMPLE 7
Solving an Equation with Fractions as Coefficients (cont’d)
1
2
x

3


  x  1  2
4
3
Check:
1
2
5

3



 5  1  2
4
3
1
2
8

 
 6   2
4
3
8 12

 2
4 3
2  4  2
The solution set of the equation is {5}.
Slide 2.3-15
CLASSROOM
EXAMPLE 8
Solving an Equation with Decimals as Coefficients
Solve.
0.5  2  3x   4.5  0.1 x  7 
Solution:
10 0.5 2  3x   10 4.5  10 0.1 x  7
5  2  5  3x   45  x  7
10 15x  x  38  x  x
10 14x 10  38 10
14 x 28

14 14
x  2
Multiplying by 10 is the same as moving the decimal point one place to the right.
Likewise, multiplying by 100 is the same as moving the decimal point two places to
the right.
Slide 2.3-16
CLASSROOM
EXAMPLE 8
Solving an Equation with Decimals as Coefficients (cont’d)
Check:
0.5  2  3x   4.5  0.1 x  7 
5  2  5 3  2   45   2  7
10   5 6  47  7
10  30  40
40  40
The solution set of the equation is {−2}.
Slide 2.3-17
Objective 3
Solve equations with no solution or
infinitely many solutions.
Slide 2.3-18
Solve equations with no solution or infinitely many solutions.
Each equation that we have solved so far has had exactly one solution. An
equation with exactly one solution is a conditional equation because it is
only true under certain conditions. Sometimes equations may have no
solution or infinitely many solutions.
Slide 2.3-19
CLASSROOM
EXAMPLE 9
Solving an Equation That Has Infinitely Many Solutions
Solve.
3x  x 10  2x  4 14
Solution:
2x 10  2x 10
2x 10  2x  2x 10  2x
10 10  10 10
00
The variable has “disappeared.” Since the last statement is true, any real
number is a solution. An equation with both sides exactly the same, is
called an identity. An identity is true for all replacements of the variables.
We write the solution set as {all real numbers}.
DO NOT write { 0 } as the solution set. There are infinitely many other
solutions. For { 0 } to be the solution set, the last line must
include a variable, such as x, and read x = 0, not 0 = 0.
Slide 2.3-20
CLASSROOM
EXAMPLE 10
Solving an Equation That Has No Solution
Solve.
3x  8  6  x 1  3x
Solution:
3x  8  6x  6  3x
3x  8  3x  3x  6  3x
8  6
Again, the variable has “disappeared,” but this time a false statement
results. When this happens in solving an equation, it indicates that the
equation has no solution and is called a contradiction. Its solution set is the
empty set, or null set, symbolized Ø.
DO NOT write { Ø } to represent the empty set.
Slide 2.3-21
Solve equations with no solution or infinitely many solutions.
The following table summarizes the solution sets of the three types of
equations presented so far.
Slide 2.3-22
Objective 4
Write expressions for two related
unknown quantities.
Slide 2.3-23
CLASSROOM
EXAMPLE 11
Translating a Phrase into an Algebraic Expression
Two numbers have a product of 36. If one of the numbers is represented by x,
find an expression for the other number.
Solution:
Slide 2.3-24