* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Hash Table
Survey
Document related concepts
Transcript
Hashing
Motivating Applications
• Large collection of datasets
• Datasets are dynamic (insert, delete)
• Goal: efficient searching/insertion/deletion
• Hashing is ONLY applicable for exact-match searching
Direct Address Tables
• If the keys domain is U Create an array T of size U
• For each key K add the object to T[K]
• Supports insertion/deletion/searching in O(1)
Direct Address Tables
Alg.: DIRECT-ADDRESS-SEARCH(T, k)
return T[k]
Alg.: DIRECT-ADDRESS-INSERT(T, x)
T[key[x]] ← x
Solution is to use hashing
tables
Alg.: DIRECT-ADDRESS-DELETE(T, x)
T[key[x]] ← NIL
•
Running time for these operations: O(1)
Drawbacks
>> If U is large, e.g., the domain of integers, then T is large (sometimes infeasible)
>> Limited to integer values and does not support duplication
Direct Access Tables: Example
Example 1:
Example 2:
U is the domain
K is the actual
number of keys
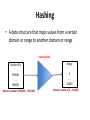
Hashing
• A data structure that maps values from a certain
domain or range to another domain or range
Hannah
Hash function
3
Dave
Adrien
f(x)
Donald
Ed
15
Domain: String values
20
55
Domain: Integer values
Hashing
• A data structure that maps values from a certain
domain or range to another domain or range
Hash function
Student IDs
Range
950000
…..
960000
0
…..
10000
Domain: numbers [950,000 … 960,000]
Domain: numbers [0 … 10,000]
Hash Tables
• When K is much smaller than U, a hash table
requires much less space than a direct-address table
– Can reduce storage requirements to |K|
– Can still get O(1) search time, but on the average case,
not the worst case
Hash Tables: Main Idea
•
Use a hash function h to compute the slot for each key k
•
Store the element in slot h(k)
•
Maintain a hash table of size m T [0…m-1]
•
A hash function h transforms a key into an index in a hash table T[0…m-1]:
h : U → {0, 1, . . . , m - 1}
•
We say that k hashes to slot h(k)
Hash Tables: Main Idea
Hash Table (of size m)
0
U
(universe of keys)
K k1
(actual k4
keys)
k5
k2
k3
h(k1)
h(k4)
h(k2) = h(k5)
h(k3)
m-1
>> m is much smaller that U (m <<U)
>> m can be even smaller than |K|
Example
• Back to the example of 100 students, each with 9-digit SSN
• All what we need is a hash table of size 100
What About Collisions
0
U
(universe of keys)
K k1
(actual k4
keys)
k5
k2
k3
h(k1)
h(k4)
h(k2) = h(k5)
Collisions!
h(k3)
m-1
• Collision means two or more keys will go to the same slot
Handling Collisions
• Many ways to handle it
– Chaining
– Open addressing
• Linear probing
• Quadratic probing
• Double hashing
Chaining: Main Idea
•
Put all elements that hash to the same slot into a linked list (Chain)
•
Slot j contains a pointer to the head of the list of all elements that hash to j
Chaining - Discussion
• Choosing the size of the hash table
– Small enough not to waste space
– Large enough such that lists remain short
– Typically 10% -20% of the total number of elements
• How should we keep the lists: ordered or not?
– Usually each list is unsorted linked list
Insertion in Hash Tables
Alg.: CHAINED-HASH-INSERT(T, x)
insert x at the head of list T[h(key[x])]
• Worst-case running time is O(1)
• May or may not allow duplication based on
the application
Deletion in Hash Tables
Alg.: CHAINED-HASH-DELETE(T, x)
delete x from the list T[h(key[x])]
• Need to find the element to be deleted.
• Worst-case running time:
– Deletion depends on searching the corresponding
list
Searching in Hash Tables
Alg.: CHAINED-HASH-SEARCH(T, k)
search for an element with key k in list T[h(k)]
• Running time is proportional to the length of the
list of elements in slot h(k)
What is the worst case and average case??
Analysis of Hashing with Chaining:
Worst Case
• All keys will go to only
one chain
T
0
• Chain size is O(n)
chain
• Searching is O(n) +
time to apply h(k)
m-1
Analysis of Hashing with Chaining:
Average Case
• With good hash function and uniform distribution
of keys
– Any given element is equally likely to hash into any of
the m slots
T
0
chain
chain
• All chain will have similar sizes
• Assume n (total # of keys), m is the hash table size
– Average chain size O (n/m)
chain
chain
m-1
Average Search Time O(n/m): The common case
Analysis of Hashing with Chaining:
Average Case
• If m (# of slots) is proportional to n (# of keys):
– m = O(n)
– n/m = O(1)
Searching takes constant time on average
Hash Functions
Hash Functions
• A hash function transforms a key (k) into a table address
(0…m-1)
• What makes a good hash function?
(1) Easy to compute
(2) Approximates a random function: for every input, every output is
equally likely (simple uniform hashing)
(3) Reduces the number of collisions
Hash Functions
• Goal: Map a key k into one of the m slots in the hash table
• Make table size (m) a prime number
– Avoids even and power-of-2 numbers
• Common function
h(k) = F(k) mod m
Some function or
operation on K (usually
generates an integer)
The output of the “mod” is
number [0…m-1]
Examples of Hash Functions
Collection of images
F(k): Sum of the pixels colors
h(k) = F(k) mod m
Collection of strings
F(k): Sum of the ascii values
h(k) = F(k) mod m
Collection of numbers
F(k): just return k
h(k) = F(k) mod m